■数学の教材になりうるか
○ 一般には,数学の学習としては,
記述式の問題>穴埋め式の問題>選択式の問題
の順に重宝され,>パズル>ゲームとなると数学の学習と認める人と認めない人に分かれると考えられる.
確かに,授業中にゲーム機で遊ばれては授業の妨げとなるが,ある教育的なねらいを実現する一つの手段として特定の場面で使うことは考えられる.
○ 筆者の考えでは,ナンバープレースを数学の授業で使える場面とは,高校流に言えば,「必要条件で捜査範囲を絞る」という訓練である.中学校では,必要条件,十分条件という用語は登場しないが,「かつ」や「または」を組み合わせて論理的に推論する訓練は,何にでも使える基本的な能力であると考えられる.しかも,1〜2時間は集中できるだけの集中力・忍耐力を必要とする点も評価したい.
* 順列,組合せ,置換の問題として,次のような性質がある.
(以下の議論では,初期値ごと移動させるものとする)
・1つの解行列があるとき,上中下の段内で行を入替えたものも解となる.
・1つの解行列があるとき,左右中央の段内で列を入替えたものも解となる.
・1つの解行列の3行(または3列)の段ごと入替えたものも解となる.
・1つの解行列で 1,2,3,4,...,9 を 5,3,4,...,8 などへ1対1にテキスト置換したものも解となる.
* 以下のページにおいて,上記の入替えによって得られる問題・解の各々約6千億通りを実際に示す.
また,対称形の問題については(形が崩れない範囲で)1つの原型に対して,左右・上下・縦横及び数字を入れ換えたもの(8×9!=約290万通り)を実際に示す.
|
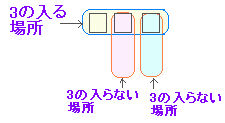
※ 要素の個数が有限個の集合においては,条件を満たさないものを消去していけば,残ったものが解といえる.
※(私見)
ナンバープレースの問題をコンピュータで解くのはNP問題(≒総当たりが避けられない問題)になるという論調の記事が多く見られるが,解がただ一つ存在する問題を解くには1秒も要しない.(入力には約30秒要する)
もう少し詳しく言えば,このサイトでは途中経過もただ一つに定まる問題だけを扱っている.したがって,私のサイトの「問題作成」ページで解けない問題はおそらく,「ある曲面で複数個の分岐が残って,実際にそのうちの一方に進めば矛盾に当たり,他方のみが有効となる形の問題」(背理法を用いる問題)だと考えられる.
このような問題を除けば,問題を解くのは「人が行うことをそのままコンピュータにたどらせるようにすれば」糸口から順にほどけるように解ける.ただし,これは必ずしも多くの人に認められている考え方ではないので一応眉につばを付けて保留にしておかれる方が無難かも.
|