|
�y���3�z
�����ǂ�
(2018�N�x �������������Z�������)
�i�j
�@�O�p��OABC�ƎO�p��ODEF�̑�����́C5:2�����炻�̑̐ϔ�͎O�p��125:8 �@Q:P=(125−8):8=117:8 ���������� |
|
��♥♫♦∀���Z�����̊�{�`�W��∳♣♬∅♠
������Ƒ̐ϔ�
�y�����z
(1)�@�Q�̐}�`�̑����䂪m : n�ł���Ƃ��C�����̖ʐϔ�́Cm2 : n2 (2)�@�Q�̗��̂̑����䂪m : n�ł���Ƃ��C�����̑̐ϔ�́Cm3 : n3 • �E�}1�ɂ����āC���F�̉~���Ɛ��F�̉~�����C r:R=ℓ:L=1:2�̑����}�`�ł���Ƃ� �@�\�ʐς̔��1:4 �@�̐ς̔��1:8 • �E�}2�ɂ����āC���F�̋��Ɛ��F�̋����C r:R=2:3�̑����}�`�ł���Ƃ� �@�\�ʐς̔��4:9 �@�̐ς̔��8:27 |
|
�y���1�z
�����ǂ�
�@���̂Ƃ��C�l�p��P�Ǝl�p��Q�̑̐ϔ�����߂Ȃ����B (2022�N�x ��茧�������Z�������)
|
|
�y���2�z
�����ǂ�
(2022�N�x ���������������Z�������)
�i�j
�����䂪1:2������C�̐ς�8�{����i���j |
|
�y���3�z
�����ǂ�
(2018�N�x �������������Z�������)
�i�j
�@�O�p��OABC�ƎO�p��ODEF�̑�����́C5:2�����炻�̑̐ϔ�͎O�p��125:8 �@Q:P=(125−8):8=117:8 ���������� |
|
�y���4�z
�����ǂ�
(2017�N�x ���ꌧ�������Z�������)
�i�j
�����䂪�C2 : 3������C���̑̐ϔ��8 : 27 �~����B�̑̐ς�V�Ƃ����� �@40 : V=8 : 27 |
|
�y���5�z
�����ǂ�
�@����(1)�C(2)�̖₢�ɓ����Ȃ����B (1)�@�O�p��P�̑̐ς����߂Ȃ����B (2)�@�O�p��P�̑��ʂ̂����C�ʐς��ő�ƂȂ�l�p�`�ƍ����Ȏl�p�`���ʂƂ��Ƃ���l�p (2019�N�x �{�錧�������Z�������)
�i�j
(1) �O�����̒藝���g���āC��ʂ̎c��̕ӂ̒��������߂�D ��ʐς� �O�p��P�̑̐ς� (2) |
|
�y���6�z
�����ǂ�
�@���̂Ƃ��C�����P�`�S�̖₢�ɓ����Ȃ����B �P�@�}�U�́C�}�T�̗����̂���C�O�p �@���̂Ƃ��C�S�_B, D, E, G�_�Ƃ��闧�̂̕\�ʐς����߂Ȃ����B �@���̂Ƃ��C�U�_I, J, K, L, M, N�_�Ƃ��闧�̂̑̐ς����߂Ȃ����D �S�@�� (2018�N�x �{�茧�������Z�������)
�i�j
�P BD, DE, EB�́C��������P�ӂ̒�����10cm�̐����`�̑Ίp��������C���̒����� ���������āC���O�p�`���(��) �Q �@�P�̌��ʂɂ��C�P�ӂ̒����� �@���̐��O�p�`�̍����́C�O�����̒藝���g���ċ��߂��� �P�̐��O�p�`�̖ʐς� ���߂�\�ʐς� �R ���_��D, E, G�Ƃ����ꍇ�����l������C�S�̎O�p������菜���ƁC�S�̂̂W���̂S�C���Ȃ킿�����̑̐ς���菜�����i�c��j�D �@���̎O�p��BDEG�́C������ABCD-EFGH����ABDE�ɓ������O�p�����S��菜�������̂����� �@���߂�̐ς� �i�ʉ��j JKLM�́C�P�ӂ̒����� |
|
�y�O�p���̑̐ς��Q�ʂ�̋��ߕ��ŏ����z
�@�@(��ʐ�)�~(����)��3 �ŋ��߂���̂ŁC�E�}�̂悤�ȎO�p���̏ꍇ�́C �����藧�D �@����𗘗p����C����h2�����m���̂Ƃ� �ɂ���ċ��߂���D |
|
�y���7�z
�����ǂ�
�@���̂Ƃ��C����(1)�C(2)�̖₢�ɓ����Ȃ����B (1)�@��DEF�̖ʐς����߂Ȃ����B (2)�@����BD��ɓ_G���CBG : GD=1 : 3�ƂȂ�悤�ɂƂ�B �@�܂��C��CF��ɓ_H���C �@�@4�_D, E, F, G������łł���O�p �A�@3�_D, E, H��ʂ镽�ʂƓ_G�Ƃ̋��������߂Ȃ����B (2018�N�x �������������Z�������)
�i�j
(1) 1�ӂ̒�����6(cm)�̐��O�p�`������C����h�͎O�����̒藝�ŋ��܂� �ʐς� �@�@(1)�̌��ʂ���C�O�p��DEFG�̒�ʐς� �@�����́C �@�̐ς́C �����`ADEB�̑Ίp��DB�́C�����`ADEB�Ɠ������ʏ�ɂ��邩��C�O�p��DEFG�ƎO�p��DEHG�Ƃ́C��ʂ����ʂ���DEG�ō���(h)�͓������D���������āC�̐ς��������D �@�����ŁCDE�̒��_��M�Ƃ����ƁC������ ���߂鍂����H�Ƃ����� |
|
�y���8�z
�����ǂ�
�@AP : PC=AQ : QD=3 : 1�ł���Ƃ���B���̂Ƃ��C�O�p��A−BPQ�̑̐ς́C�l�p��B−PCDQ�̑̐ς̉��{���C���߂Ȃ����B (2019�N�x �H�c���������Z�������)
�i�j
• �O�p���C�l�p���̑̐ς́C(��ʐ�)�~(����)��3 ������
�@��APQ�Ǝl�p�`PCDQ���ʂƂ݂Ȃ��ƁC���_B�܂ł̍����͋��ʂɂȂ�B���������āC�O�p��A−BPQ�Ǝl�p��B−PCDQ�Ƃ̑̐ϔ�́C��APQ�Ǝl�p�`PCDQ�̖ʐϔ�ɓ������D�@�@(����)�������Ȃ�C�̐ϔ��(��ʐ�)�̔�ɂȂ� �@�@(��ʐ�)�������Ȃ�C�̐ϔ��(����)�̔�ɂȂ� �@AP : PC=AQ : QD=3 : 1�ł��邩��C�ʐϔ�� �@��APQ : ��ACD=32 : 42=9 : 16 �@��APQ : ⏢PCDQ=9 : 7 ���������� �@��APQ ÷ ⏢PCDQ=
• ���Ƃ����L���́C�O�p�`�Ɠǂ݁C�ǂ̋��ȏ��ł��g���Ă��܂��D
• ���Ƃ����L���́C�l�p�`�Ɠǂ݂܂����C�`�Ƃ��Ă͐����`���g���Ă��܂��D • ⏥�Ƃ����L���́C���s�l�ӌ`�Ɠǂ݁C�����̋��ȏ��Ŏg���Ă��܂��D • ��`��\���L����⏢�ł����C�Ή�����t�H���g��\���ł��邩�ǂ����͋@��Ɉˑ����邩������܂���D • ���s�l�ӌ`�ł��Ȃ���`�ł��Ȃ��P�Ȃ�l�p�`��\���L���́C�����̕����R�[�h�ɂ͂Ȃ��悤�ł��D |
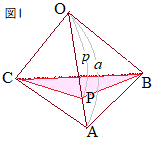 (1)�@�E�}1�̂悤�ȎO�p��OABC�ɂ����āCOA : OP=a : p�ƂȂ�_��P�Ƃ���Ƃ��C�O�p��OABC�ƎO�p��OPBC�̑̐ϔ��
(1)�@�E�}1�̂悤�ȎO�p��OABC�ɂ����āCOA : OP=a : p�ƂȂ�_��P�Ƃ���Ƃ��C�O�p��OABC�ƎO�p��OPBC�̑̐ϔ��a : p
�ɓ������D
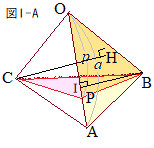 (1)�̍l����
(1)�̍l�����@�E�}�̂悤�ɁC��OAB����OPB���ʂƂ��āCCH�����ʂ̍����Ƃ���O�p���O�p��OABC�ƎO�p��OPBC���l����ƁC���������ʂ�����C�̐ϔ�͒�ʐς̔�ɂȂ�D �@��ʐ���OAB����OPB�́C�O�p�`�Ƃ��Ă̍�����BI�ŋ��ʂ�����C�ʐϔ�͒�ӂ̒����̔�OA : OP=a : p�ɂȂ�D �@���������āC�O�p��OABC�ƎO�p��OPBC�̑̐ϔ�́Ca : p�ɂȂ�D 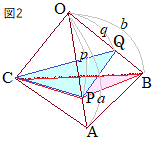 (2)�@�E�}2�̂悤�ȎO�p��OABC�ɂ����āCOA : OP=a : p�ƂȂ�_��P�Ƃ��COB : OQ=b : q�ƂȂ�_��Q�Ƃ���Ƃ��C�O�p��OABC�ƎO�p��OPQC�̑̐ϔ��
(2)�@�E�}2�̂悤�ȎO�p��OABC�ɂ����āCOA : OP=a : p�ƂȂ�_��P�Ƃ��COB : OQ=b : q�ƂȂ�_��Q�Ƃ���Ƃ��C�O�p��OABC�ƎO�p��OPQC�̑̐ϔ��ab : pq
�ɓ������D
�@(1)�̂Ƃ��Ɠ��l�ɂ��āC�O�p��OPBC�ƎO�p��OPQC�̑̐ϔ���l����ƁCC������OAB�ɂЂ��������̒��������ʂ̍����ɂȂ邩��C�̐ϔ����OPB����OPQ�̖ʐϔ�b : q�ɓ������D �@�O�p��OABC�ƎO�p��OPBC�́Ca : p �@�O�p��OPBC�ƎO�p��OPQC�́Cb : q �ł��邩�� �@OABC : OPQC=ab : pq �ɓ������D • (�O�p��OPBC)=(�O�p��OABC)�~ �@(�O�p��OPQC)=(�O�p��OPBC)�~ �@(�O�p��OPQC)=(�O�p��OABC)�~ |
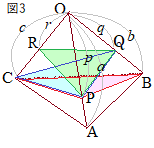 (3)�@�E�}2�̂悤�ȎO�p��OABC�ɂ����āCOA : OP=a : p�ƂȂ�_��P�COB : OQ=b : q�ƂȂ�_��Q�COC : OR=c : r�ƂȂ�_��R�Ƃ���Ƃ��C�O�p��OABC�ƎO�p��OPQR�̑̐ϔ��
(3)�@�E�}2�̂悤�ȎO�p��OABC�ɂ����āCOA : OP=a : p�ƂȂ�_��P�COB : OQ=b : q�ƂȂ�_��Q�COC : OR=c : r�ƂȂ�_��R�Ƃ���Ƃ��C�O�p��OABC�ƎO�p��OPQR�̑̐ϔ��abc : pqr
�ɓ������D
�@(�O�p��OPQR)=(�O�p��OABC)�~
�Ə����Ă��悢�D�����̎��͋��ȏ��ɏ�����Ă��Ȃ�����C�u�o���Ă��邩��K���K���|��������O�v�Ƃ��������œ����̓��Ăɏ����ƁC���_�̉\������D���Ȃ킿�C�����ߖ���I����ł́C�r���o�߂������Ȃ�����C�ق��Ďg���Ă�������Ȃ����C�L�q�����Ăł́C�u���������ʂȏꍇ�́C�̐ϔ�͒�ʐς̔�ɓ������v�Ȃǂ��ȒP�ȍ����C���Ȃ��Ƃ������v�Z���x�͎����K�v������D 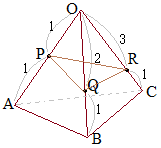 �y��1�z
�y��1�z�@�E�}�̎O�p��OABC�ɂ����āCOP:PA=1:1, OQ:QB=2:1, OR:RC=3:1�̂Ƃ��C �@�̐ςɂ��� • (OPQR) =(OABC)�~ • (OPQR):(PQR-ABC)=1:(4−1)=1:3 ����`�̂悤�Ȍ`�ɘf�킳�ꂸ�ɁC�Q�̎O�p���̑̐ς̍����l����Ƃ悢�D 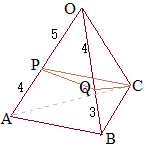 �y��2�z
�y��2�z�@�E�}�̎O�p��OABC�ɂ����āCOP:PA=5:4, OQ:QB=4:3�̂Ƃ��C �@�̐ςɂ��� • (OPQC) =(OABC)�~ • (OPQC):(PQCAB)=20:(63−20)=20:43 ����`�̂悤�Ȍ`�ɘf�킳�ꂸ�ɁC�Q�̎O�p���̑̐ς̍����l����Ƃ悢�D �y���8�z �@�̐ςɂ��� • (ABPQ):(BPCDQ)=9:(16−9)=9:7 |
|
�y���9�z
�����ǂ�
�@���̂Ƃ��C���̖₢(1)�E(2)�ɓ�����B (1)�@���̕��́C�_B�ƕ���ADFC�Ƃ̋����ɂ��ďq�ׂ����̂ł���B�������@�@�@�ɓ��Ă͂܂���̂��C����(�A)�`(�I)����P�I�ׁB
�@�@�@�@��G�Ƃ���Ƃ��C����BG�̒������C�_B�ƕ���ADFC�Ƃ̋����ł���B
(�A)�@��AC�̒��_(�C)�@��CF�̒��_ (�E)�@����AF�Ɛ���CD�Ƃ̌�_ (�G)�@��CBE�̓����ƕ�CF�Ƃ̌�_ (�I)�@�_B�����AC�ɂЂ��������ƕ�AC�Ƃ̌�_ (2)�@2�_H, I�����ꂼ���AC, DF���CH=DI= (2022�N�x ���s�{�������Z�������)
�i�j
(1)→(�I)
�@(�A)�`(�G)�����łȂ����Ƃ́C���炩�ł��邪�C(�I)�Œ�܂�_G�ɂ��āCBG⊥AC�́C�����Ɍ����邪�C����BG������ADFC���̂ǂ̒����ɂ������ł��邱�Ƃ�b���Β����Ȃ肻��
(2)(1)�̌��ʂ���C⏥CHDI���ʂƂ����Ƃ��̎l�p��BCHDI�̍����́C �@4 : BG= �@ |
|
�y���10�z
�����ǂ�
�@��BC, CD�̒��_�����ꂼ��P, Q�C�_Q����AP�ɂЂ���������AP�Ƃ̌�_��R�Ƃ���D���̃A�`�G�ɓ����Ȃ����B �A�@AQ�̒��������߂Ȃ����B �C�@��APQ�̖ʐς����߂Ȃ����B �E�@QR�̒��������߂Ȃ����B �G�@�O�p����RBCD�̑̐ς́C���l�ʑ�ABCD�̑̐ς̉��{���C���߂Ȃ����B (2018�N�x �X���������Z�������)
�i�j
�A AC=8cm, CQ=4cm������C���p�O�p�`��ACQ�ɎO�����̒藝��K�p����� �@AQ= �C �@AP=AQ= �@PQ= PQ�̒��_��M�Ƃ����� �@MQ=2(cm) ���p�O�p�`��AMQ�ɎO�����̒藝��K�p����� �@AM= �@��APQ= �E �G �O��̃E�̌��ʂ�p����� ���������� �O�p����RBCD�͐��l�ʑ�ABCD�ƒ�ʐς������ō�����6����1������C�̐ς� |
|
|