|
1
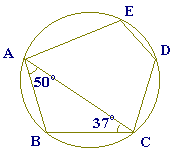
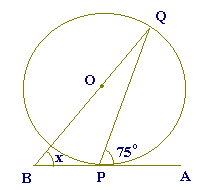
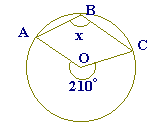 右の図において,点A,B,Cは円Oの周上の点である.∠xの大きさを求めなさい.
右の図において,点A,B,Cは円Oの周上の点である.∠xの大きさを求めなさい.
|
2
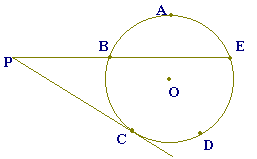
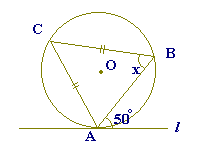 右の図で直線l は円Oの接線で,点Aがその接点である.
右の図で直線l は円Oの接線で,点Aがその接点である.
CA=CBのとき,∠xの大きさを求めなさい. |
|
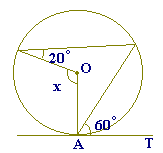
3
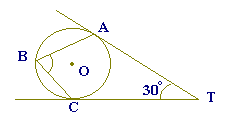
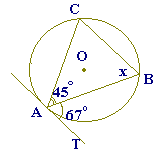 右の図で,3点A,B,Cは円Oの周上にあり,ATは点Aにおける円Oの接線である.∠xの大きさを求めなさい.
右の図で,3点A,B,Cは円Oの周上にあり,ATは点Aにおける円Oの接線である.∠xの大きさを求めなさい.
|
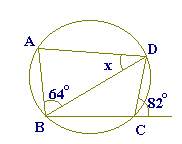
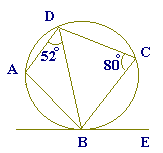 4
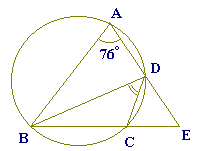
4右の図のように,AD//BCである台形ABCDが円に内接している.点Bにおける円の接線をBEとし, ∠BCD=80゜, ∠ADB=52゜であるとき, ∠CBEの大きさを求めよ. |
 5
5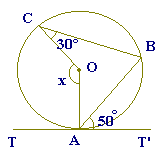 6
6
 7
7
 8
8
 9
9
 10
10
 11
11
 12
12