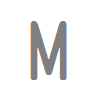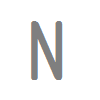|
線対称な図形
[解説]
ある直線を折り目として折り返したとき,両側の図形がピッタリと重なる図形を線対称な図形といい,このときの直線を対称軸といいます。 ○次の例1では,対称軸が1本あります。  例2    
【例1】
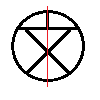
次の記号はいずれも線対称な図形である.  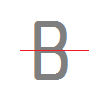 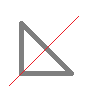  左右対称な場合だけでなく,上下対称の場合や斜めの直線に関して対称な場合もあるので,「試しに調べてみる」ことが重要
【例2】
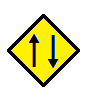
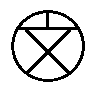
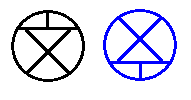
次の記号はいずれも線対称な図形である. 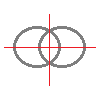 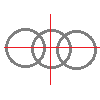 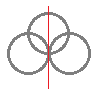  左の2個は対称軸が2つあるのに対して,右の2つは対称軸は1つである
点対称な図形
[解説]○次の図のように,ある点を中心に180°回転させたとき,元の図形と一致する図形を点対称な図形といいます。 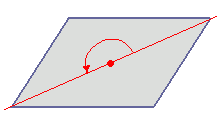 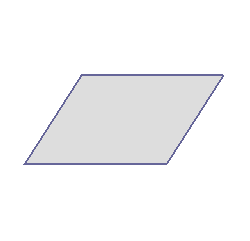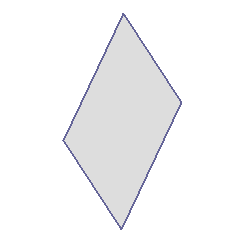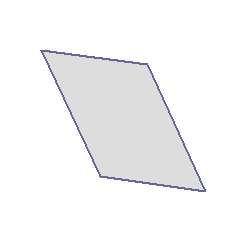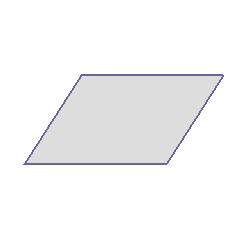
右の図は平行四辺形が対角線の交点を対称の中心とする点対称な図形であることを示しています。 |
○点対称な図形では,次の図のように1つの点から対称の中心を突き抜けて向こう側に同じ距離だけ進むと対応する点があります。
それぞれの点に対応する点があります。 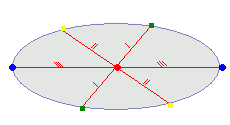
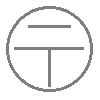
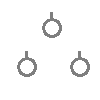
※ 花火のように広がる図形・放射状図形は,点対称と間違わないように気をつけましょう。右の図は点対称な図形ではありません。
180°回転しても元の図形と一致しない。 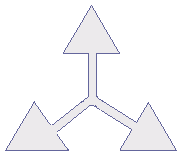
【例1】
例えば,正三角形上の点1から中心までの距離 -”- を中心の反対側に伸ばした点1’は元の正三角形の上になく,点2から中心までの距離 -o- を中心の反対側に伸ばした点2’も元の正三角形の上にない.正三角形は点対称な図形ではない. このため,元の正三角形(灰色)を180°回転すると青の正三角形になり,元の図形と一致しない. だから,正三角形は点対称な図形ではない.  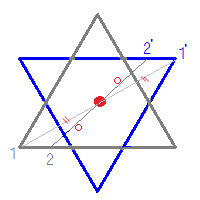
【例2】
例えば,正方形上の点1から中心までの距離 -”- を中心の反対側に伸ばした点1’は元の正方形の上にあり,点2から中心までの距離 -o- を中心の反対側に伸ばした点2’も元の正方形の上にある.正方形は点対称な図形である. このように,元の正方形(灰色)を180°回転すると元の図形と一致する. だから,正方形は点対称な図形である.  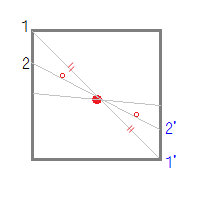
【例3】
例えば,正五角形上の点1から中心までの距離 -”- を中心の反対側に伸ばした点1’は元の正五角形の上になく,点2から中心までの距離 -o- を中心の反対側に伸ばした点2’も元の正三角形の上にない.正五角形は点対称な図形ではない. このため,元の正五角形(灰色)を180°回転すると青の正五角形になり,元の図形と一致しない. だから,正五角形は点対称な図形ではない.  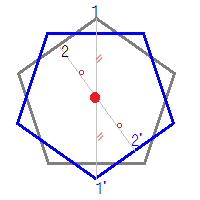
【例4】
例えば,正八角形上の点1から中心までの距離 -”- を中心の反対側に伸ばした点1’は元の正八角形の上にあり,点2から中心までの距離 -o- を中心の反対側に伸ばした点2’も元の正八角形の上にある.正八角形は点対称な図形である. このように,元の正八角形(灰色)を180°回転すると元の図形と一致する. だから,正八角形は点対称な図形である. 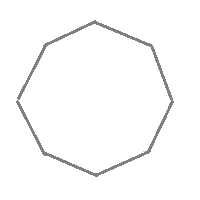 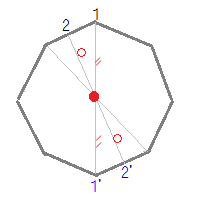
【例5】
例えば,正九角形上の点1から中心までの距離 -”- を中心の反対側に伸ばした点1’は元の正九角形の上になく,点2から中心までの距離 -o- を中心の反対側に伸ばした点2’も元の正九角形の上にない.正九角形は点対称な図形ではない. このため,元の正九角形(灰色)を180°回転すると青の正九角形になり,元の図形と一致しない. だから,正九角形は点対称な図形ではない. 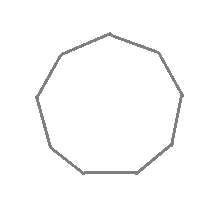 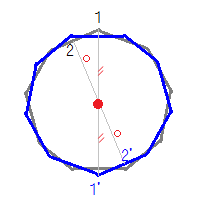 |