|
���̕łł́C���̍��ڂɂ��āC����Ɨ��K��肪����܂��D���̕\�͒��ڃW�����v�ł��郁�j���[�ɂȂ��Ă��܂��D |
|
�K���̕�
�y���P�z
�i�j
�\
�@�E���\�́C�N���X�̑S���k36�l���̃n���h�{�[�������̋L�^���܂Ƃ߂��x�����z�\�ł���B���̂Ƃ��C����(1)�`(3)�ɓ�����B
(1)�@�K���̕��͉������B (2)(3)�@�� �i���茧2017�N�������j
(1)�@���̗�̂悤�Ɏ������������̂�x�����z�\�ƌ����C���ꂼ��̊K���̊Ԋu�̑傫�����u�K���̕��v�Ƃ����܂��D |
�i�[���l����l�ցj
����K����5�ȏ�10�����i���Ȃ킿5��x<10�j��������C10�͂��̊K���ɓ����Ă��Ȃ��̂ł͂Ȃ����C���ۂɂ͏����_�ȉ���2�ʁi0.01m=1cm�j���x�܂ł�������Ȃ�����C�傫�����̒[��9.99�܂ł����Ȃ��̂ł͂Ȃ��̂��H�Ƌ^���l�� �ȏ� �` ���� 5 �` 10 10 �` 15 15 �` 20 … �ƂȂ��Ă���Ƃ��C�K���̕��́u����K���̐擪�̒l�v����u���̊K���̐擪�̒l�v�܂ł̊Ԋu�ƍl���܂��D������C���̕\�ŐԂŎ������l�̊Ԋu�ɂȂ�̂ŁC 5����10�܂ł̊Ԋu��5�ɂȂ�܂��D  �i�悭�����b�j
�i�悭�����b�j���s���́C�E�}�̂悤�ɍs�̐擪�ʒu���玟�̍s�̐擪�ʒu�܂łő���܂��D�����T�C�Y�ł͂Ȃ��D |
|
�y���P�z
�@�E�̕\�́C�N���X�̑S���k27�l���̐g�����܂Ƃ߂��x�����z�\�ł���B�K���̕��͉�cm���B
|
�y���Q�z
�@�E�̕\�́C�N���X�̑S���k25�l���̐��w�̓��_���܂Ƃ߂��x�����z�\�ł���B�K���̕��͉��_���B
�����������l����Ȃ�Ƃ��ɁC���̂悤�ȏ�����������ꍇ������܂����C�K���̕��́u���ꂼ��̊K���̐擪�̒l�v����u���̊K���̐擪�̒l�v�܂łő���܂��D
1�_����21�_�Ȃǂ���C21−1=20 20�_…�i���j |
|
�K���l
�y���Q�z
�i�j
�@�E�̕\�́C�N���X�̑S���k27�l���̐g�����܂Ƃ߂��x�����z�\�ł���B�K���l�̗��i�A�`�G�j�߂Ȃ����B
���ꂼ��̊K���̒����̒l�i���[�̒l�𑫂��ĂQ�Ŋ������l�j���K���l�Ƃ����܂��D ��̕\�ŁC�A��(150+160)��2=155�ł��D ���l�ɂ��āC�C�C�E�A�G�͏���165, 175,185�ɂȂ�܂��D �E�̕\�̂悤�ɁC�K��������ɂȂ�Ƃ��́C�K���l�͏����ɂȂ�܂������C�Ŏg���܂��D
|
�y���R�z
�@�E�̕\�́C�N���X�̑S���k35�l���̑̏d���܂Ƃ߂��x�����z�\�ł���B�A�̗��ɓ��鐔�����Ȃ����B
|
|
�m��\�l - - - ���ϒl�C�����l�C�ŕp�l�n �@�����S�̂̓������P�̒l�ŕ\������������\�l�Ƃ����܂��D �@��\�l�ɂ��u���ϒl�v�u�����l�v�u�ŕp�l�v�u�͈́v�Ȃǂ�����܂��D
�@�u�^����1�����łȂ���Ȃ�Ȃ��v�Ȃǂƌ��߂��Ă͂����܂���D�ǂ̑�\�l�������Z��������C�e�����������g���ĕ��͂������Ƃ��ɁC�˂炢���������邽�߂Ɉ�ԓK������\�l��I��Ŏg���悤�ɂ��܂��D
�@�͈͎͂����́u�U����v��\���܂��D ���ϒl
(1)�@�u���ϒl�v�Ƃ́C�����̒l�̍��v��x���̍��v�Ŋ��������̂������܂��D
�y��z4�̐��l
|
���̕\�ł́C
2.5�̎�����1�C���v2.5
�����̌��̍��v10�C�����̒l�̍��v110������C���ϒl��110��10=11.0�ƂȂ�܂��D
7.5�̎�����3�C���v22.5 12.5�̎�����4�C���v50.0 17.5�̎�����2�C���v35.0 ���̂悤�ɁC�x�����z�\���畽�ϒl�����߂�Ƃ��́C�i�K���l�j�~�i�x���j�̌v�Z���J��Ԃ��s���̂ŁC���̕\�̂悤�Ɂi�K���l�j�~�i�x���j�̗���t�������āC���Ɋ|���Z�����Ă���C�c�ɑ����̂����ʂł��D
|
|
���ȉ��Ɉ��p���Ă���������ł́C���̖��͋L�q�����ł����C��������ł̓ǎ҂̑��쐫���悭���邽�߂ɁC���̃T�C�g�ł́C�Ǝ��ɑI����ɂ��Ă��܂��D�I�����̒����琳�������̂��P�N���b�N���Ă��������D����I�����ɋ^�₪����Ƃ��́C������҂�ς킷���ƂȂ��C���̃T�C�g�̊Ǘ��l�Ɏ��₵�Ă��������D
�y���S�z
�@���̕\�́C����N���X�̐��k30�l���P�����ɓǂ{�̍������܂Ƃ߂����̂ł���B �@���̂Ƃ��C���̃N���X�̐��k��1�����ɓǂ{�̍����̕��ϒl�����߂Ȃ����D
�i���m��2017�N�������j
���̖��ł́C�K���l�������Ƃ��Ē��ڗ^�����Ă���ƍl���āC���̂悤�Ɂi�����j�~�i�x���j�̗���lj����āC�c�ɂ����Ă��牡�ɑ����Ƃ悢�ł��傤�D
|
�y���T�z
�@20�l�̐��k�ɁC20�_���_�̊����̏������e�X�g���s���C���̌��ʂ��E�̕\�ɂ܂Ƃ߂��B�������C���_�͂��ׂĐ����̒l�ł������B���̕\����l�����镽�ϓ_�̍ł��傫�ȏꍇ�̒l�ƍł������ȏꍇ�̒l�̍����@�_�ł���B
�i���R����������2017�N�������j
�@�����C�x�����z�\�ɐ������ꂽ�����̕��ϒl�́C�K���l�~�x�����g���Čv�Z����̂������̗��ł���Ɖ��߂���ƁC���̖��ł������ϓ_�̍���������]�n�͂Ȃ��Ȃ�D
�@�����ŁC�u���ꂼ��̊K���̎����͂��̊K���l�ɂ�����̂Ƃ݂Ȃ��v�Ƃ����ʏ�̌v�Z���@���̗p�����ɁC�u�����������ϒl�͎����̒l�̑��a��x���̍��v�Ŋ������l�Ƃ���v�Ƃ������n�I�Ȓ�`�ɗ����߂��čl���܂��D
����́C���ʂɓ���b�ł͂���܂���D���͂ɏ�����Ă���u��C��ǂ߂v�N�ł�������͂��ł��D
�@���_�͐����l�ł���Ƃ������Ƃ���C�Ⴆ��20�_�����Ƃ�19�_�ȉ��̂��Ƃł��D�����Łu�e�K���̐l�������ׂčő�l���Ƃ��Ă���ꍇ�v�Ɓu���ׂčŏ��l���Ƃ��Ă���ꍇ�v�̕��ϒl�����߂�Ƃ悢�D
���̕\�ɂ��C�ő�̏ꍇ�̕��ϒl�����߂�� (20×3+...+7×4)��20 =278��20=13.9 �ŏ��̏ꍇ�̕��ϒl�����߂�� (20×3+...+0×4)��20 =224��20=11.2 13.9−11.2=2.7…�i���j |
|
�����l
(2)�@������傫���̏��ɕ��ׂ��Ƃ��C�����ɂ���l���u�����l�v�i�܂��́u���W�A���v�j�Ƃ����܂��D
�Z��ʂɁC�����̌�����̏ꍇ�́C�傫�������琔���Ă������������琔���Ă������ɗ���l���P�Ɍ��܂�C���̒l�������l�ł��D
�y��z5�l�̑̏d(kg) �Z�����̌��������̏ꍇ�́C�u�����ɕ��ԂQ�̒l�̕��ρv�𒆉��l�Ƃ��܂��D �y��z6�l�̑̏d(kg)
���̎������Ȃ��āC�x�����z�\����������Ƃ��́C���̊K���̒��Ɏ������ϓ��ɕ��z���Ă�����̂Ƃ��Ē����l�����߂܂��D �E�̕\�ł́C���v13�̒����͏�����������7�Ԗځi�傫��������V�Ԗځj�̎���������C10�`15�̊K���̏�����������2�Ԗڂ̒l�ƍl���܂��D �K����5�̊Ԋu��5�̎������ϓ��ɕ���ł���Ƃ���ƁC��1������C10,11,12,13,14�̂悤�ɕ���ł�����̂Ɓu���Ȃ��܂��v�D����2�Ԗڂ̒l�C11�������l�ł��D |
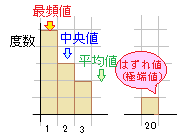 �Z�e���т̔N���̂悤�ɁC�Ꮚ���w�����|�I�ɑ������ɂP�l�������z�����҂�����ꍇ
�Z�e���т̔N���̂悤�ɁC�Ꮚ���w�����|�I�ɑ������ɂP�l�������z�����҂�����ꍇ���ϒl�́u�ɒ[�l�v�u�͂���l�v�̉e�����Ĉ��������₷���C�Ⴆ���钬���̔N���̕��z���E�}�̂悤�ł���Ƃ��i�P��100���~�j�C�v�Z��͕��ϒl��336���~�ƂȂ��Ă��C�قƂ�ǂ̐��т̎����͕��ϒl�������Ȃ��Ȃ�܂��D ����ɑ��Ē����l�͏��Ȃ�������́i�܂��͑���������́j���ʂȂ̂ŁC���z�����҂̔N����1000���~�ł����Ă��C�P���~�ł����Ă����̋��z�̉e���͎܂���D 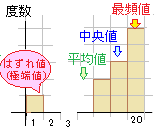 �Z��̗�Ƃ͋t�ɁC�ȒP�ȕ��K�e�X�g�̂悤�ɂقƂ�ǂ̐��k�����_�ɂȂ�C�ɒ[�ɂł��Ȃ����k���P�l�������Ȃ��悤�ȏꍇ�ɂ́C�قƂ�ǂ̐��k�͕��ϒl�����������_�ɂȂ��Ă��܂��D
�Z��̗�Ƃ͋t�ɁC�ȒP�ȕ��K�e�X�g�̂悤�ɂقƂ�ǂ̐��k�����_�ɂȂ�C�ɒ[�ɂł��Ȃ����k���P�l�������Ȃ��悤�ȏꍇ�ɂ́C�قƂ�ǂ̐��k�͕��ϒl�����������_�ɂȂ��Ă��܂��D
|
|
�y���U�z
20 ,40 ,80 ,60 ,80 ,
�@�E�̎����́C���w�Q�N��10�l���s�����C����Q�[���̓��_�̋L�^�ł���B���̎����ɂ��āC���̊e��ɓ����Ȃ����B30 ,60 ,50 ,90 ,20 (1)�@�� (2)�@10�l�̋L�^�̒����l�����߂Ȃ����B �i�O�d��2017�N�������j
�����������珇�ɕ��ׂ��
(50+60)��2=55…�i���j |
�y���V�z
�@�E�̕\�́C�R�N�����q�S��50�l�̈��͂̋L�^���C�x�����z�\�ɂ܂Ƃ߂����̂ł���B
�@����50�l�̋L�^�̒����l���ӂ��ފK���ɂ��āC�K���l���Ȃ����B �i�R����2017�N�������j
�@�����l�����߂�ƌ����Ă���̂ł͂Ȃ����Ƃɒ��ӁD�܂��u�����l���܂ފK�������߂āv�C���Ɂu���̊K���l����v�Əq�ׂĂ���̂ł��D
�@�S�̂�50�l�̎���������C�����͑O����25�Ԗڂ�26�Ԗڂ̊Ԃł��D �@18�`22�̊K���܂łɗݐς�12�l�C22�`26�̊K���܂œ����Ɨݐς�26�l�ɂȂ邩��C�����l���܂ފK���́u22�`26�̊K���v �@���ɁC���̊K���̊K���l��(22+26)��2=24(kg)…�i���j |
|
�ŕp�l
(3)�@�x�����z�\�ŁC�x�����ł������K���̊K���l���u
���x�����z�\�ɐ�������Ă��Ȃ����̎����C�Ⴆ�Ύ��̗�̂悤�Ȏ����ɂ��Ă͍ŕp�l�͍l���܂���D
�y��z5�l�̑̏d(kg)
�E�̓x�����z�\�ɂ����ēx���̈�ԑ����l15���ŕp�l���ƌ����Ă���̂ł͂���܂���D �x������ԑ����K���̊K���l52.5���ŕp�l�ł��D
�E�̕\�͂���y�Y���X�̂P���̔���グ��x�����z�\�ɐ����������̂��Ƃ��܂��D ���̕\����u�������500�~����700�~�̉��i�сC���Ȃ킿�K���l600�~�̉��i�сv���ƌ����܂��D ���̓y�Y���X�Ƃ��ẮC����̉��i�т̏��i�𑝂₻���Ȃǂƍl����Ƃ悢�D |
�Z�E�̕\�̂悤�ɁC�x�����ő�ƂȂ�K�����P�łȂ��Ƃ��́C�ŕp�l�͂P�Ɍ��炸�C500��700���ŕp�l�ɂȂ�܂��D
���y�Y���X�̔���グ��\�ɂ�����L�̂`�\�Ƃa�\���ׂĂ݂�ƁC�ŕp�l�͊K���̋����ɂ���ĕς��C���̐��̎��������Ō��܂��ł͂Ȃ��ƌ����܂��D 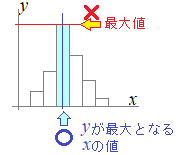
��
�ŕp�l�́C�x��y�̍ő�l�ł͂Ȃ��D
y���ő�ƂȂ�x�̒l�F�悭����鉿�i�сi�̊K���l�j ��
�ŕp�l�́C�x�����z�\�̋����ɂ���ĕς��D
|
|
�y���W�z
�@�E�̕\�́C����N�̂Q���̍Œ�C���ׂāC�x�����z�\�ɐ����������̂ł���B�Œ�C���̍ŕp�l�����߂Ȃ����B
�i������2017�N�������j
�x�����ł������l�i���̕\�ł� 9�j���ŕp�l�Ȃ̂ł͂���܂���D
�x�����ő�ƂȂ�K���̊K���l���ŕp�l�ł��D
���������āC2�`4�i��C�j�̊K���̊K���l�����߂܂��D (2+4)��2=3(��C)…�i���j |
�y���X�z
�\
�@�E���\�́C�N���X�̑S���k36�l���̃n���h�{�[�������̋L�^���܂Ƃ߂��x�����z�\�ł���B���̂Ƃ��C����(1)�`(3)�ɓ�����B
(2)�@�ŕp�l�i���[�h�j�͉������B (1)(3)�@�� �i���茧2017�N�������j
�x�����ł������l�i���̕\�ł� 15�j���ŕp�l�Ȃ̂ł͂���܂���D
�x�����ő�ƂȂ�K���̊K���l���ŕp�l�ł��D
���������āC10�`15�im�j�̊K���̊K���l�����߂܂��D (10+15)��2=12.5(m)…�i���j |
|
�͈�
(4)�@�����̒��̍ő�l�ƍŏ��l�̍����u�͈��v�i�����W�j�Ƃ����܂��D
�y��z5�l�̑̏d(kg)�����̒l�ł���Ƃ�
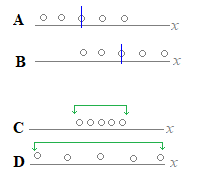 �͈͂��傫����C�����͍L���U����Ă��邱�ƂɂȂ�C�͈͂���������Ύ����͖��ɏW�܂��Ă��邱�ƂɂȂ�܂��D���̂悤�ɁC�͈͂ɂ���Ď����́u�U����v��\�����Ƃ��ł��܂��D
�͈͂��傫����C�����͍L���U����Ă��邱�ƂɂȂ�C�͈͂���������Ύ����͖��ɏW�܂��Ă��邱�ƂɂȂ�܂��D���̂悤�ɁC�͈͂ɂ���Ď����́u�U����v��\�����Ƃ��ł��܂��D�@�E�}�ɂ����āZ��������\���Ă���Ƃ��C �@�`�����a�̕������ϒl�⒆���l�͑傫���i�E���ɂ���j���͈͓͂������炢���ƌ����܂��D �@�b�����c�̕����͈͂��傫���i�U����Ă���j�����ϒl�⒆���l�͂قړ������炢���ƌ����܂��D
�Ⴆ���̐}�ɂ����āZ���}���\���I��̃^�C����\���Ă���Ƃ��C�c�̂悤�ȕ��z�ɂȂ��Ă���Ɠ��H�̒ʍs�K�����ԍs��Ȃ���Ȃ�Ȃ����ƂɂȂ�܂��D
|
�y���10�z
20 ,40 ,80 ,60 ,80 ,
�@�E�̎����́C���w�Q�N��10�l���s�����C����Q�[���̓��_�̋L�^�ł���B���̎����ɂ��āC���̊e��ɓ����Ȃ����B30 ,60 ,50 ,90 ,20 (1)�@10�l�̋L�^�͈̔͂����߂Ȃ����B (2)�@�� �i�O�d��2017�N�������j
|
|
���Γx��
�Z�x�����z�\�ɂ����āC�e�K���̓x����x���̍��v�Ŋ��������̂����Γx���Ƃ����܂��D�Z���ꂼ��̊K���ɓx����Ή��������\���x�����z�\�ł���̂ɑ��āC���ꂼ��̊K���ɑ��Γx����Ή��������\�����Γx�����z�\�Ƃ����܂��D �Z���Γx���i���Γx�����z�\�j���g���Ɣ䗦�̔�r���ȒP�ɂł��܂��D
���̓x�����z�\�𑊑Γx�����z�\�ɏ���������ƉE�̂悤�ȕ\�ɂȂ�܂��D
���x���̍��v��100������C���ꂼ��̓x����100�Ŋ���Ƒ��Γx���ɂȂ� |
�y���R�z
�i�j
�@�E�̕\�́C�`�Z�̐��k80�l�Ƃa�Z�̐��k210�l�̂�����̒ʊw���Ԃ�x�����z�\�ɂ܂Ƃ߂����̂ł���B�Q�Z�ɂ��āC�ʊw���Ԃ�15���ȏ�20�������̐��k�̊������傫���̂͂`�Z�Ƃa�Z�̂ǂ���ł��邩�B�������f�������R�Ƃ��킹�ď����Ȃ����B
�i�ΐ쌧2017�N�������j
�ʊw���Ԃ�15���ȏ�20�������̐��k�̊�����
�`�Z��20��80=0.25
���������āC�`�Z�̕����������傫��
�a�Z��42��210=0.2 |
|
�y���11�z
�@�E�̕\�́C���钆�w�Z�̂Q�N���q40�l�̑��蕝���т̋L�^��x�����z�\�ɐ����������̂ł���B
�@330cm�ȏ�360cm�����̊K���̑��Γx�������߂Ȃ����B �i�x�R��2017�N�������j
|
�y���12�z
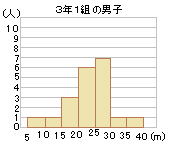
�@�E�̐}�́C���钆�w�Z��3�N1�g�̒j�q20�l��3�N2�g�̒j�q20�l�̃n���h�{�[�������̋L�^���C���ꂼ��q�X�g�O�����ɕ\�������̂ł���B�Ⴆ�C3�N1�g�̒j�q�̃q�X�g�O�����ɂ����āC25�`30�̊K���ł́C�n���h�{�[�������̋L�^��25m�ȏ�30m�����̒j�q��7�l���邱�Ƃ�\���Ă��܂��B
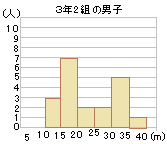 �@3�N1�g��3�N2�g�̒j�q�̍��v40�l�̋L�^���C�K�����E�̐}�Ɠ����q�X�g�O�����ɕ\�����Ƃ��C
�@3�N1�g��3�N2�g�̒j�q�̍��v40�l�̋L�^���C�K�����E�̐}�Ɠ����q�X�g�O�����ɕ\�����Ƃ��C�@�@�� �A�@�����l�������Ă���K���̑��Γx�������߂Ȃ����B �i�F�{��2017�N�������j
�@40�l�̒����l�͏��Ȃ�������20�Ԗڂ�21�Ԗڂ̊Ԃ�����C�����Ŏ�����20�`25�̊K���ɂȂ�D �@���̊K���̑��Γx���� 8��40=0.2…�i���j |
|
���܂Ƃ߂̖�聡
�y���13�z
�}�Q
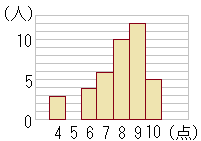
�@����N���X�̐��k40�l�Ɏ��{�����e�X�g�̓��_���q�X�g�O�����ɕ\���ƁC�}�Q�̂悤�ɂȂ����B���̂Ƃ��C���ϒl�C�����l�i���W�A���j�C�ŕp�l�i���[�h�j�̑召�W�𐳂����\�������̂��C���̃A�`�G����P�I��ŁC���̕����������Ȃ����B �A�@�i���ϒl�j<�i�����l�j<�i�ŕp�l�j �C�@�i�����l�j<�i���ϒl�j<�i�ŕp�l�j �E�@�i�ŕp�l�j<�i���ϒl�j<�i�����l�j �G�@�i�ŕp�l�j<�i�����l�j<�i���ϒl�j �i���Ɍ�2017�N�������j
�܂��C�ŕp�l��9
���ɁC�����l�͓��_�̒Ⴂ������20�l�ڂ�21�l�ڂ̊Ԃ����� 8 ���ϒl�́C(�K���l�~�x���̘a)��(�x���̘a)�ɂ���Čv�Z���܂��D (4×3+6×4+7×6+8×10+9×12+10×5)��40 =316��40=7.9 �ȏ�ɂ��C�i���ϒl�j<�i�����l�j<�i�ŕp�l�j→�A…�i���j |
�y���14�z
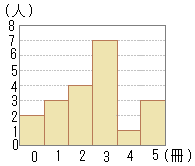
�@�E�̐}�́C����N���X�̐��k20�l���~�x�ݒ��ɓǂ{�̍������C�q�X�g�O�����ɕ\�������̂ł���B����20�l���ǂ{�̍����ɂ��ďq�ׂ����Ƃ��ēK�Ȃ��̂��C���̃A�`�G�̂�������P�I�сC�����œ����Ȃ����B �A�@���z�͈̔́i�����W�j�́C4���ł���D �C�@ �E�@�����l�i���W�A���j�́C3���ł���D �G�@���ϒl�́C2.3���ł���B �i��t��2017�N�������j
�͈͂́C�����̒��̍ő�l�i5���j�ƍŏ��l�i0���j�̍�������C5−0=5�i���j…�A�́~
�ő�l�ƍŏ��l�Ƃ����Ă��C�x���i�}�̏c�����̖ڐ���j�̍ő�l(8)�ƍŏ��l(1)�̍��̂��Ƃł��Ȃ��I
�ŕp�l�Ƃ́C�x�����ł������K���̊K���l�̂��Ƃ�����C3��…�C�́~�����̒l�i�}�̉������̖ڐ���j�̍ő�l�i5���j�ƍŏ��l�i0���j�̍��̂���
�ł������x���i�c�����̖ڐ���j�ł͂Ȃ��C�x�����ł������K���̊K���l�i���̐}�ł͉������̖ڐ���j
20�l�̎����̒����l�́C���Ȃ�������10�Ԗڂ�11�Ԗڂ̊Ԃ�����C�}����3���̊K���ɓ���܂�…�E�́Z���ϒl�� (0�~2+1�~3+2�~4+3�~7+4�~1+5�~3)��20=2.55…�G�́~ |
|
�ގ����.�������K
�@�E�̓x�����z�\�́C���钆�w�Z�̂P�N�����q40�l�̗������Ƃт̋L�^���܂Ƃ߂����̂ł���B�x�����ł������K���̑��Γx�������߂Ȃ����B �i�Ȗ،�2018�N�������j
�i���Γx���j=�i�e�K���̓x���j���i�x���̍��v�j
�@�x�����ł������K���́C130�ȏ�150�����̊K���ŁC���̓x����12�@�x���̍��v��40 ���߂鑊�Γx���� |
�@�E�̕\�́C���钆�w�Z�̃o���[�{�[������30�l�̐g�����܂Ƃ߂��x�����z�\�ł���B �@�g����170cm�ȏ�̐l���́C���̃o���[�{�[������30�l�̉����ɂȂ邩�C���߂Ȃ����B �i��t��2018�N�������j
|
�@�E�̕\�́C���钆�w�Z�̃o���[�{�[������30�l�̐g�����܂Ƃ߂��x�����z�\�ł���B �@�g����170cm�ȏ�̐l���́C���̃o���[�{�[������30�l�̉����ɂȂ邩�C���߂Ȃ����B �i�����s2018�N�������j
|
�@�E�̕\�́C���钆�w�Z�̐��k30�l�̒ʊw���Ԃ�x�����z�\�ɂ܂Ƃ߂����̂ł���B �@�@�\����[�@�@]�ɓ����̂ɓK���Ă��鐔�������Ȃ����B �A�@���̃A�`�G�̂����C10���ȏ�15�������̊K���̑��Γx���Ƃ��Đ��������̂͂ǂ�ł����B��I�сC�L�������ň݂͂Ȃ����B �A�@6�@�@�C�@30�@�@�E�@0.2�@�@�G�@0.6 �i���{2018�N�������j
|
�@�E�̕\�́C���钆�w�Z�̃n���h�{�[�������̋L�^���C�x�����z�\�ɕ\�������̂ł��B���̃N���X�̃n���h�{�[�������̋L�^�̕��ϒl���C�x�����z�\���狁�߂Ȃ����B �i��ʌ�2018�N�������j
�@
�ŋ��߂���D
�K���l �@���������āC���̓x�����z�\���畽�ϒl�����߂�Ƃ��� �̌������g���D �@ |
�@�E�̓x�����z�\�́C����N���X�̐��k20�l�̃n���h�{�[�������̋L�^���܂Ƃ߂����̂ł���B�x�����z�\���狁�ߋL�^�̕��ϒl���Ȃ����B �P�D 21.0m�@�Q�D 21.2m �R�D 21.4m�@�S�D 21.6m �i�_�ސ쌧2018�N�������j
|
|
�y���2.7�z
�����ǂ��@���̐}�́C�N���X�̐��k33�l���ċx�݂ɓǂ{�̍������C�q�X�g�O�����ɕ\�������̂ł���B���̃q�X�g�O�����ɂ����āC���ϒl��a�C�����l��b�C�ŕp�l��c�Ƃ���Ƃ��Ca, b, c�̊W��\���s�����Ƃ��čł��K�Ȃ��̂��C���Ƃ̃A�`�E����1�I�сC�L���œ����Ȃ����B 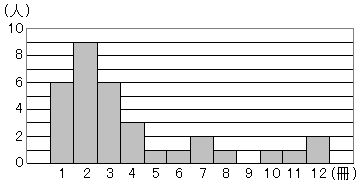 �i�R�`��2018�N�������j
�����ϒl��
�������l�́C������������14�ԁi=�傫��������14�ԁj�̃f�[�^��������K���l������ ���ŕp�l�͓x���̍ł������K���l������ �ȏォ�� c<b<a→�E…�i���j |
�@�E�̎����́C�֓�7�s���̂͂������̏o�חʂ��܂Ƃ߂����̂ł���C���̕��́C�L�u���������w�̎��Ƃł��̎����ɂ��Ęb���������Ƃ��̉�b�̈ꕔ�ł���B���(1)�C(2)�̖₢�ɓ����Ȃ����B �L�u����F
���̎����̑�\�l�Ƃ��Ăǂ�Ȓl���g���������ȁB
�D�q����F
��\�l�ɂ́C���ϒl��(�A)�����l�C�ŕp�l��������ďK������ˁB���ȏ��ɂ́C���ϒl����\�l�Ƃ��Ă悭�g������Ă�������B
�ǒj����F
�ł��C(�C)���̎����̕��z���ƁC���ϒl�͑�\�l�Ƃ��Ăӂ��킵���Ȃ��Ǝv����B
(2)�@�������i�C�j�̂悤�ɂ�����̂͂Ȃ����C���̎����������z�̓����ɒ��ڂ��āC�������Ȃ����B �i�Q�n��2018�N�������j
�i�A�j
�@���̎��������ڗ^�����Ă���Ƃ��C������傫���̏��ɕ��ׂĒ����ɂȂ�l���u�����l�v�Ƃ����D�i������̂Ƃ��͒����l�͌��������ŕ�����D������̂Ƃ��́C������2�̒l�̂������ɂȂ�̂ŁC�����Q�̕��ϒl�𒆉��l�Ƃ���D�j �˂��̎����ł͍�ʌ��̏o�חʂ������ɂȂ�i�傫��������4�ԖځC������������4�Ԗځj����C14000(t)…�i���j
�u������傫���̏��ɕ��ׂĒ����ɂȂ�l�𒆉��l�Ƃ����v�̒�`����C��ʌ��������l�Ȃ̂ł͂Ȃ��C14000(t)�������l�ɂȂ邱�Ƃɒ���
�i�C�j�@���̎����̂悤�ɁC�ɒ[�ɑ傫�Ȓl�i��錧�̒l�j���܂܂�Ă���ꍇ�ɁC���ϒl���\�l�Ɏg���ƁC���̑�\�l�͈�錧�̒l�Ɉ��������đ��̌��̒l�Ɩ��W�Ȓl�ɂȂ�₷������…�i���j
�@���̂悤�ȋɒ[�l���܂܂�鎑���̗�Ƃ��āC�N���̕��ϒl�͑�\�l�Ƃ��Ăǂ��Ȃ̂��Ƃ����c�_���悭����D
�Ⴆ�C����5���т̔N�����C�e�X1���~�C200���~�C200���~�C200���~�C200���~�̂Ƃ��C���̒����̔N���̕��ϒl��2160���~�ƂȂ邪�C���̔N���͒N�̔N���ɂ��߂��Ȃ��D���ۂɂ́C���̕��ϒl�̂�����2000���~��1�l�̉e���ŁC160���~���c��4�l�̉e���ɂȂ��Ă���D �@���̂悤�ɁC��\�l�ɕ��ϒl���g���Ƌɒ[�l�i�O��l�Ƃ������j�̉e�����₷���D �@����ɑ��āC��\�l�ɒ����l���g���Ƌɒ[�l�i�O��l�Ƃ������j�̉e�����ɂ����D |
|
�y���2.9�z
�����ǂ��@���钆�w�Z�̑̈�̎��ƂŁC2km�̎��v�����s�����B �@���̐}�́C�P�g�̒j�q16�l�ƂQ�g�̒j�q15�l�̋L�^�����ꂼ��q�X�g�O�����ɕ\�������̂ł���B �@����(1)�C(2)�ɓ����Ȃ����B 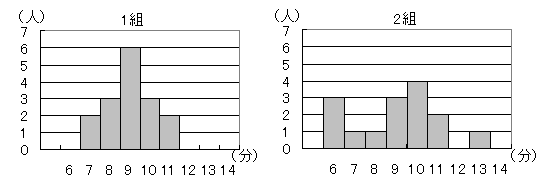
�A�@�͈͂��傫���̂͂Q�g�ł���B
(1)�@�s�̉w�`���ɏo�ꂷ�邽�߂ɁC�P�g�ƂQ�g�����킹��31�l�̋L�^���悢���ɕ��ׁC���6�l���\�I��ɑI�B����6�l�̂����C�P�g�̑I��̋L�^�̕��ϒl��7��10�b�C�Q�g�̑I��̕��ϒl��6��40�b�ł���Ƃ��C��\�I��6�l�̋L�^�̕��ϒl�͉������b���C���߂Ȃ����B�C�@11���ȏ�12�������̊K���̑��Γx���͓����ł���B �E�@���ϒl�C�����l�C�����Ђ��ŕp�l�̂R�̒l���C�قړ����l�ɂȂ�̂́C�Q�g�ł���B �G�@�����l���܂܂��K���́C�P�g���Q�g�������ł���B �I�@�ŕp�l���傫���̂͂P�g�ł���B �i�a�̎R��2018�N�������j
(1)
�A�@�i�͈́j=�i�ő�l�j−�i�ŏ��l�j������C�P�g�̋L�^�͈̔͂�11−7=4�C�Q�g�̋L�^�͈̔͂�13−6=7 �͈͂͂Q�g�̕����傫������C�A�́� �C�@11���ȏ�12�������̊K���̑��Γx���́C�P�g�ł� �G�@�����l���܂܂��K���́C�P�g�Q�g�Ƃ�9���ȏ�10������������C�G�́� �I�@�P�g�̍ŕp�l��9��30�b�C�Q�g�̍ŕp�l��10��30�b������C�I�́~ �ȏ�ɂ��C�K�Ȃ��̂́C�A�G…�i���j (2) 8��������6�l�ɂȂ邩��C��\�I��̂����łP�g��2�l�C�Q�g��4�l�ɂȂ�D (7��40�b�~2+6��40�b�~4)��6=6��50�b…�i���j |
�y���2.10�z
�����ǂ��@ 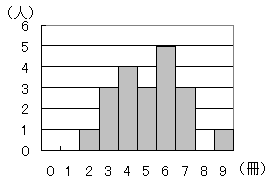 �@����N���X�̐��k20�l�ɂ��āC�P�����Ԃɓǂ{�̍����������B�E�̐}�́C���̌��ʂ��q�X�g�O�����ɕ\�������̂ł���B
�@����N���X�̐��k20�l�ɂ��āC�P�����Ԃɓǂ{�̍����������B�E�̐}�́C���̌��ʂ��q�X�g�O�����ɕ\�������̂ł���B�@���̖₢�ɓ�����B (1)�@���̃A�`�G�̂����C���������̂͂ǂꂩ�B�K���Ȃ��̂��P�I�сC���̋L���������B
�A�@�ŕp�l�C���ϒl�C�����l�̂����C�ł��������͕̂��ϒl�ł���B
(2)�@�P�����Ԃɓǂ{�̍�����7���ȏ�ł��������k�̐l���́C�S�̂̉������B�C�@�ŕp�l�C���ϒl�C�����l�̂����C�ł��傫���̂͒����l�ł���B �E�@�ŕp�l�͕��ϒl��菬�����B �G�@���ϒl�͒����l���傫���B �i���Q��2018�N�������j
(1)
���ϒl�� (2�~1+3�~3+4�~4+5�~3+6�~5+7�~3+9�~1)��20=5.1�i���j �ŕp�l�� 6�i���j �����l�� ���Ȃ�������11��(����������11��)������5�i���j �� �������̂̓G…�i���j (2) 4��20=0.2 → 20�i%�j…�i���j |