|
�y�v�_�z
(1)�@�O�p�`�̓��p�̘a��180���ɓ������D (2)�@�O�p�`�̊O�p�́C����Ɨׂ荇��Ȃ��Q�̓��p�̘a�ɓ������D 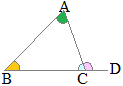 (1)�@��̐}�ɂ�������A+��B+��C=180�� (2)�@��̐}�ɂ�������ACD=��A+��B |
 �y���P�z
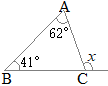
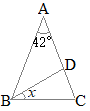
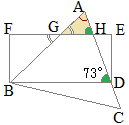
�y���P�z�@�E�̐}�̂悤����ABC������܂��B��x�̑傫�������߂Ȃ����B �i�k�C��2017�N�������j
�O�p�`�̊O�p�́C����Ɨׂ荇��Ȃ��Q�̓��p�̘a�ɓ��������� ��x=62��+42��=103��…�i���j �i�ʉ��j �O�p�`�̓��p�̘a��180���ɓ��������� 62��+42��+��C=180�� ��C=77�� �䂦�� ��x=180��−77��=103��…�i���j |
 �i�j
�i�j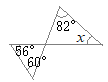
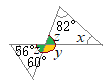 �O�p�`�̓��p�̘a��180��������
�O�p�`�̓��p�̘a��180��������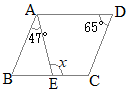
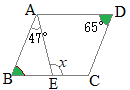 �i�j
�i�j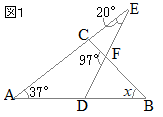
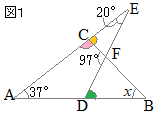
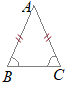 ����
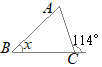
����
 �i�j
�i�j
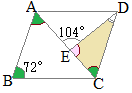 �i�j
�i�j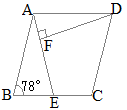
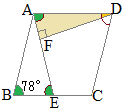 �i�j
�i�j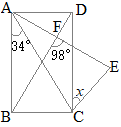
 �i�j
�i�j ����
����
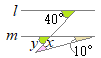 �i�j
�i�j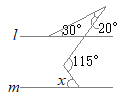
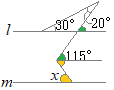 �i�j
�i�j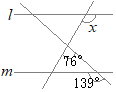
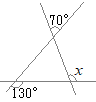
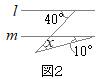
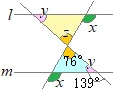 �i�j…�E�}�̐��F�̎O�p�`�ōl����ꍇ
�i�j…�E�}�̐��F�̎O�p�`�ōl����ꍇ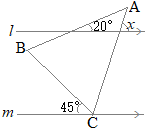
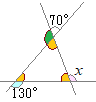
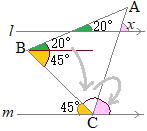 �i�j…�E�}�̂悤��
�i�j…�E�}�̂悤��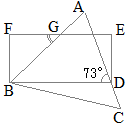
 �i�j…�E�}�̂悤��
�i�j…�E�}�̂悤��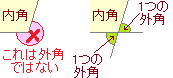 �����ꂼ��̓��p�ɑ��āC�O�p�͂Q������܂����C�u�O�p�̘a�v�Ƃ����Ƃ��͂��̂���1���̘a�������܂��D
�����ꂼ��̓��p�ɑ��āC�O�p�͂Q������܂����C�u�O�p�̘a�v�Ƃ����Ƃ��͂��̂���1���̘a�������܂��D
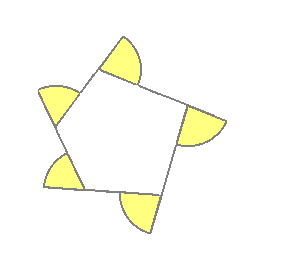 �i����j
�i����j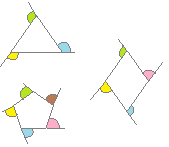 ����
����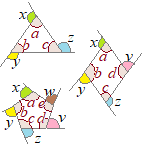 �i���1�j
�i���1�j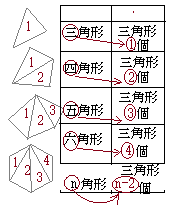 �i���2�j
�i���2�j �i���2�j
�i���2�j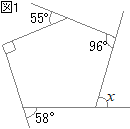
 �i�j
�i�j
 �i�j
�i�j
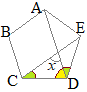 �i�j
�i�j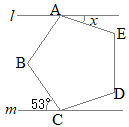
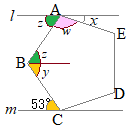 �i�j
�i�j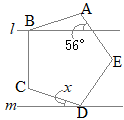
 �i�j
�i�j
 �i�j
�i�j