|
【要点】
△ABC の AB,AC の中点をそれぞれ M,N とするとき, MN//BC …(1) MN= BC …(2) が成り立ちます. これを「中点連結定理」といいます. |
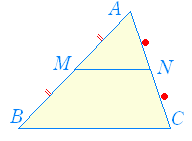 -- 図1 -- MN:BC=1:2になります. また,∠AMNと∠ABCとは等しいから,MN//BCになります. |
|
|
|
【要点】
△ABC の AB,AC の中点をそれぞれ M,N とするとき, MN//BC …(1) MN= BC …(2) が成り立ちます. これを「中点連結定理」といいます. |
 -- 図1 -- MN:BC=1:2になります. また,∠AMNと∠ABCとは等しいから,MN//BCになります. |
 【問題1】 【問題1】
|
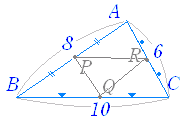
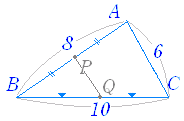 △ABC において AB,BC の中点がそれぞれ P,Q だから,
△ABC において AB,BC の中点がそれぞれ P,Q だから,PQ//AC …(1) PQ= AC …(2) が成り立ちます. (2)から,PQ=3 同様にして,QR= BA=4 , RP= CB=5 も成り立ちます. |
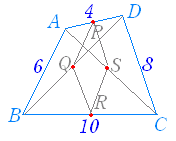 【問題2】 【問題2】
|
|
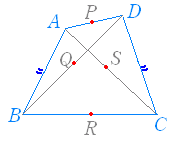
△ABD に中点連結定理を適用すると PQ= AB=3 △ABC に中点連結定理を適用すると SR= AB=3 また △BCD に中点連結定理を適用すると QR= DC=4 △ACD に中点連結定理を適用すると PS= DC=4 が成り立ちます. |
(補助線を引く)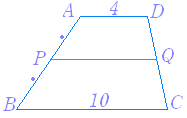 【問題3】 【問題3】
|
|
対角線 AC と PQ の交点を R とすると, 「平行線と線分の比」の性質から 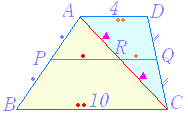 AP:PB=AR:RC=DQ:QC=1:1 AP:PB=AR:RC=DQ:QC=1:1△ABC に中点連結定理を適用すると PR= BC=5 △ACD に中点連結定理を適用すると RQ= AD=2 が成り立ちます. したがって,PQ=5+2=7 |
(補助線を引く)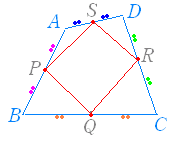 【問題4】 【問題4】
|
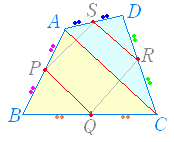 △ABC に中点連結定理を適用すると
△ABC に中点連結定理を適用するとPQ//AC PQ= AC △BCD に中点連結定理を適用すると SR//AC SR= AC が成り立ちます. PQ//AC , AC//SR より PQ//SR PQ= AC , SR= より PQ=SR これにより,向かい合う1組の辺 PQ , SR が平行でかつ長さが等しいことが言えます. ※ この問題では「向かい合う1組の辺が平行でかつ長さが等しい → 平行四辺形」という定理を使ったが,「2組の向かい合う辺がそれぞれ平行 → 平行四辺形」という定理を使って証明するときは,次の(A)のように書けばよい.また,「2組の向かい合う辺の長さがそれぞれ等しい → 平行四辺形」という定理を使って証明するときは,次の(B)のように書けばよい. (A) PQ//AC , SR//ACより PQ//AC QR//BD , PS//BDより QR//BD 以上により 2組の向かい合う辺がそれぞれ平行だから PQRS は平行四辺形 (B) PQ= AC , SR= ACより PQ=SR QR= BD , PS= BDより QR=PS 以上により 2組の向かい合う辺の長さがそれぞれ等しいから PQRS は平行四辺形 |
 【問題5】 【問題5】
|
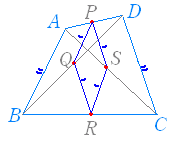 PQ= AB=SR
PQ= AB=SRQR= DC=PS さらに AB=CD だから PQ=QR=RS=SP が成り立つ 4辺の長さが等しい四角形は「ひし形」と呼ばれる. |
|
|