← PC用は別頁
※中学３年生向け「２次関数」について，このサイトには次の教材があります．
この頁へGoogleやYAHOO ! などの検索から直接来てしまったので「前提となっている内容が分からない」という場合や「この頁は分かったがもっと応用問題を見たい」という場合は，他の頁を見てください．　 が現在地です．


...（携帯版）メニューに戻る...(ＰＣ版)メニューに戻る

== ２次関数と直線で作られる図形の面積 ==

《問題》
１
右の図で，曲線は関数ｙ＝のグラフであり，２点Ａ，Ｂはこの曲線と直線ｙ＝８との交点で，点Ａからｘ軸に垂線ＡＣをひきます．また点Ｐは，この曲線上を原点Ｏから点Ｂまで動きます．△ＰＡＣと△ＰＡＢの面積が等しくなるとき，点Ｐの座標を求めなさい．
（「H11埼玉県　高校入試問題」の引用）

■考え方

△ＰＡＣ，△ＰＡＢの面積をＰのｘ座標で表わし，これらが等しくなるようなｘを求めます．
△ＰＡＣにおいて，ＡＣを底辺とし，ＰからＡＣまでの距離を高さと考えると，底辺ＡＣ＝８
また，ｙ＝８とｙ＝の交点を求めると，(－４，８)，(４，８)になるから，
高さをＰのｘ座標ｘを用いて表わすと［ア］
ゆえに，△ＰＡＣ＝８(［ア］)÷２・・・(1)
［ア］に入るものを，次のうちからクリック↓
ｘ－４ｘ＋４
△ＰＡＢにおいて，ＡＢを底辺とし，ＰからＡＢまでの距離を高さと考える．
Ｐのｙ座標をｘで表わすとだから，
高さは［イ］，ＡＢ＝８
ゆえに，△ＰＡＢ＝８(［イ］)÷２･･･(2)
［イ］に入るものを，次のうちからクリック↓
８－ ８＋
(1)(2)が等しくなるようなｘの値を求めると
８(ｘ＋４)÷２＝８(８－)÷２　より　ｘ＋４＝８－
ｘ２＋２ｘ－８＝０
ｘ＝－４，２
ここで，点Ｐは，この曲線上を原点Ｏから点Ｂまで動くのだから，０≦ｘ≦４
ゆえに，ｘ＝［ウ］
［ウ］に入るものを，次のうちからクリック↓

－４ ２ ８


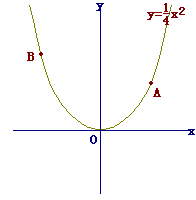
２
　右の図のように，関数ｙ＝のグラフ上に２点Ａ，Ｂがあり，点Ａ，Ｂのｘ座標はそれぞれ４，－６である．
　関数ｙ＝のグラフ上に点Ｐをとり，２点Ａ，Ｐを通る直線がｙ軸と交わる点をＱとするとき，次の(1),(2)の問いに答えなさい．ただし，点Ｐのｘ座標は点Ａのｘ座標より大きいものとする．
(1)　点Ｐのｘ座標が６であるとき，点Ｑのｙ座標を求めなさい．
(2)　点Ａが線分ＰＱの中点となるとき，△ＢＯＰと△ＡＢＱの面積の比を求めなさい．
（「H11千葉県　高校入試問題」の引用）
■考え方
以下において，解答欄に分数を記入するときは，例えば３分の５ならば　5/3　のように　分子/分母　の形で記入しなさい．例えばマイナス３分の５のように負の数になるときは，　-5/3　のように　符号を分子に付けなさい．
(1)
　点Pはｙ＝上の点だから，そのｘ座標が６のとき，ｙ座標は［ア］になる．
同様に，点Ａのｙ座標は［イ］になる．
［ア］＝
［イ］＝

２点Ａ，Ｐを通る直線の方程式をｙ＝ａｘ＋ｂとおいて，係数ａ，ｂを求めると，
点Ｐを通ることから，
９＝６ａ＋ｂ・・・＜1＞
点Ａを通ることから，
４＝４ａ＋ｂ・・・＜２＞
連立方程式＜１＞＜２＞を解くと，ａ＝［ウ］，ｂ＝［エ］だからＱのｙ座標は［エ］である．
［ウ］＝
［エ］＝

(2)
　点Ａ（４，･･･）が線分ＰＱの中点となるとき，Ｐのｘ座標は［オ］で，ｙ座標は［カ］である．
２点Ａ，Ｐを通る直線の方程式をｙ＝ａｘ＋ｂとおいて，係数ａ，ｂを求めると，
点Ｐを通ることから，
16＝８ａ＋ｂ・・・＜３＞
点Ａを通ることから，
４＝４ａ＋ｂ・・・＜４＞
連立方程式＜３＞＜４＞を解くと，ａ＝［キ］，ｂ＝［ク］だからＱのｙ座標は［ク］である．
［オ］＝
［カ］＝
［キ］＝
［ク］＝

　△ＢＯＰの面積は，次の図のＤＯを底辺とする２つの三角形，△ＤＢＯと△ＰＤＯの面積の和と考えることができる．
　２点Ｐ，Ｂを通る直線の方程式を求めてＤのｙ座標を求める：
２点Ｂ，Ｐを通る直線の方程式をｙ＝ａｘ＋ｂとおいて，係数ａ，ｂを求めると，
点Ｐを通ることから，
16＝８ａ＋ｂ・・・＜５＞
点Ｂを通ることから，
９＝－６ａ＋ｂ・・・＜６＞
連立方程式＜５＞＜６＞を解くと，ａ＝［ケ］，ｂ＝［コ］だからＤのｙ座標は［コ］である．
ゆえに，△ＢＯＰ＝△ＤＢＯ＋△ＰＤＯ＝［サ］
［ケ］＝
［コ］＝
［サ］＝

　同様にして，△ＡＢＱの面積は，次の図のＥＱを底辺とする２つの三角形，△ＥＢＱと△ＡＥＱの面積の和と考えることができる．
　２点Ａ，Ｂを通る直線の方程式を求めてＥのｙ座標を求める：
２点Ａ，Ｂを通る直線の方程式をｙ＝ａｘ＋ｂとおいて，係数ａ，ｂを求めると，
点Ａを通ることから，
４＝４ａ＋ｂ・・・＜７＞
点Ｂを通ることから，
９＝－６ａ＋ｂ・・・＜８＞
連立方程式＜７＞＜８＞を解くと，ａ＝［シ］，ｂ＝［ス］だからＥのｙ座標は［ス］である．
ゆえに，△ＡＢＱ＝△ＥＢＱ＋△ＡＥＱ＝［セ］
［シ］＝
［ス］＝
［セ］＝
以上により，△ＢＯＰ：△ＡＢＱ＝［サ］：［セ］＝［ソ］：［タ］
［ソ］＝
［タ］＝


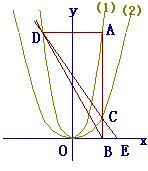
３
　右の図において，曲線(1)は関数ｙ＝ｘ２のグラフであり，曲線(2)は関数ｙ＝ａｘ２のグラフである．
　点Ａは曲線(1)上にあり，そのｘ座標は３である．点Ｂはｘ軸上にあり，線分ＡＢはｙ軸に平行で，点Ｃは曲線(2)と線分ＡＢとの交点である．
　また，点Ｄは曲線(1)上にあり，線分ＡＤはｘ軸に平行である．直線ＣＤの傾きは－１であり，点Ｅは直線ＣＤとｘ軸との交点である．
　原点をＯとするとき，次の問いに答えなさい．
(ア)　曲線ｙ＝ａｘ２のａの値を求めなさい．
(イ)　三角形ＡＣＤと三角形ＢＤＥの面積の比を最も簡単な整数の比で表わしなさい．
（「H11神奈川県　高校入試問題」の引用）
■考え方
分かるものから順に座標を記入していく．
Ａのｘ座標が３だから，
  • Ａのｙ座標は［あ］である．
  • Ｂのｘ座標は［い］で，ｙ座標は［う］である．
  • Ｄのｘ座標は［え］で，ｙ座標は［お］である．
［あ］＝
［い］＝
［う］＝
［え］＝
［お］＝

線分ＣＤ（ＤＥ）の傾きが－１で，点Ｄの座標が（え，お）であることから，直線ＣＤの方程式をｙ＝－ｘ＋ｂとおいてｂの値を求めると，ｂ＝［か］となる．これにより，
  • Ｃのｘ座標が［き］だから，ｙ座標は［く］となる．
  • Ｅのｙ座標が０だから，ｘ座標は［け］となる．
［か］＝
［き］＝
［く］＝
［け］＝
(ア)
　Ｃの座標をｙ＝ａｘ２に代入すると，ａ＝［こ］
［こ］＝

(イ)
　ＤＡ＝６，ＡＣ＝６だから△ＡＣＤ＝［さ］
　ＢＥ＝３，ＡＢ＝９だから△ＢＤＥ＝［し］
ゆえに，△ＡＣＤ：△ＢＤＥ＝［す］：［せ］
［さ］＝
［し］＝
［す］＝
［せ］＝

４ 　右の図のように，関数ｙ＝のグラフ上に，ｘ座標がそれぞれ－４，２となる２点Ａ，Ｂをとる．このとき，次の(1)，(2)の問いに答えよ．
(1)　直線ＡＢの式を求めよ．
(2)　直線ＡＢとｙ軸との交点をＣとする．また，関数ｙ＝のグラフ上に点Ｐをとって，△ＯＣＰの面積が△ＯＡＢの面積のになるようにしたい．このとき，点Ｐの座標を求めよ．ただし，Ｐは原点OとＡの間にとるものとする．
（「H11新潟県　高校入試問題」の引用）
■考え方
次の空欄を埋めなさい．例えば，答が　３分の５　のような分数になるときは　5/3　のように記入し，答が負の数になるときは -5/3　のように，符号を分子につけなさい．
(1)
　点Ａは関数ｙ＝のグラフ上にあり，ｘ座標が－４だから，ｙ座標は［ア］である．
　また，点Ｂも関数ｙ＝のグラフ上にあり，ｘ座標が２だから，ｙ座標は［イ］である．
［ア］＝
［イ］＝

　２点Ａ（－４，［ア］），Ｂ（２，［イ］）を通る直線の方程式を，ｙ＝ａｘ＋ｂとおくと，
Ａを通ることから　４＝－４ａ＋ｂ・・・＜１＞
Ｂを通ることから　１＝２ａ＋ｂ・・・＜２＞
＜１＞＜２＞より，ａ＝［ウ］，ｂ＝［エ］
ゆえに，直線の方程式は，ｙ＝［ウ］ｘ＋［エ］・・・＜３＞
［ウ］＝
［エ］＝
(2)
　切片の値ｂから，点Ｃのｙ座標は，ｙ＝［オ］

このとき， △ＯＡＢ＝△ＯＢＣ＋△ＯＣＡ
＝２・２／２＋２・４／２＝６
他方，ＰからＹ軸までの距離をｋとおくと，△ＯＣＰ＝２・ｋ／２＝ｋ
となるから，面積がになるようにするには，ｋ＝［カ］とすればよい．

ＰはＯとＡの間にあるからＰのｘ座標は，ｘ≦０
ゆえに，Ｐの座標は，ｘ＝［キ］，ｙ＝［ク］
 

［オ］＝
［カ］＝
［キ］＝
［ク］＝

...（携帯版）メニューに戻る

...メニューに戻る

■このサイト内のGoogle検索■

△このページの先頭に戻る△
【 アンケート送信 】
… このアンケートは教材改善の参考にさせていただきます

■この頁について，良い所，悪い所，間違いの指摘，その他の感想があれば送信してください．
○文章の形をしている感想は全部読ませてもらっています．
○感想の内で，どの問題がどうであったかを正確な文章で伝えていただいた改善要望に対しては，可能な限り対応するようにしています．（※なお，攻撃的な文章になっている場合は，それを公開すると筆者だけでなく読者も読むことになりますので，採用しません．）


質問に対する回答の中学版はこの頁，高校版はこの頁にあります