|
［用語］ 四角形の４つの頂点が１つの円周上にあるとき，この四角形は円に内接するといいます．
【定理】
円に内接する四角形の向かい合う内角の和は１８０゜に等しい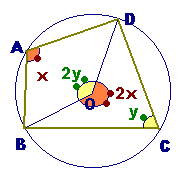．  左図の∠Aと∠Cは向かい合う内角です．左図の∠Bと∠Dも向かい合う内角です．
［解説］ ∠A＝ｘ， ∠C=y とおくと， 中心角は円周角の２倍 ２ｘ＋２ｙ＝３６０゜だから ｘ＋ｙ＝１８０゜ つまり ∠A+∠C=１８０゜ 同様にして ∠B+∠D=１８０゜も成り立ちます |
|
［用語］ 四角形の４つの頂点が１つの円周上にあるとき，この四角形は円に内接するといいます．
【定理】
円に内接する四角形の向かい合う内角の和は１８０゜に等しい． 左図の∠Aと∠Cは向かい合う内角です．左図の∠Bと∠Dも向かい合う内角です．
［解説］ ∠A＝ｘ， ∠C=y とおくと， 中心角は円周角の２倍 ２ｘ＋２ｙ＝３６０゜だから ｘ＋ｙ＝１８０゜ つまり ∠A+∠C=１８０゜ 同様にして ∠B+∠D=１８０゜も成り立ちます |
 ...（携帯版）メニューに戻る...（PC版）メニューに戻る
|