大きな区分
中学数学>> 中学３年 >>素数

== 最大公約数,最小公倍数 ==

 ■はじめに
【分数の約分】
■　分数を約分するときは，分母と分子を同じ数で割る．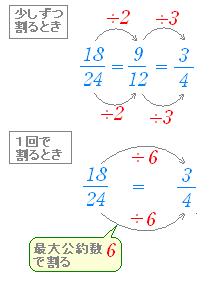

■　このときに登場する「分母と分子の共通の約数（=公約数）」の中で「最も大きな数字（=最大）」のことを「最大公約数」という．

18 の約数は，1 , 2 , 3 , 6 , 9, 18
24 の約数は，1 , 2 , 3 , 4 , 6 , 8 , 12, 24
共通の約数（=公約数） 1 , 2 , 3 , 6 の中で最大のものは 6
⇒ 最大公約数は 6

■　間違って「最小公約数」などと言わないように．最小公約数は，計算しなくても１に決まっているので「最小公約数」などという用語は使わない．（=当たり前でつまらないことだから）

■　「最大公約数」は分数の約分のときだけでなく広く使われる重要なものである．
■ ２つの数の最大公約数を求めるには，
（Ａ）　小学校のときに習った「割り算（の裏向き）」のやり方で割れるだけ割っていく方法
（Ｂ）　素因数分解を利用する方法
がある．
（Ａ）　割れるだけ割っていく方法で最大公約数を求めるには
例
2 )18 , 24
3 ) 9 , 12
↓ 3 ,_ 4
最大公約数は2×3=6
■共通に割れる数のうちで最も大きいのが最大公約数（２や３でも割れるが，これらは公約数．最大公約数は６になる．）
※最大公約数，最小公倍数は分数の約分や通分に欠かせない重要なものである．
（小学校で習っていることになっているが，今の教育課程では扱いが薄いという印象を受ける．）
【分数の通分】
　分数を通分するときは，２つの分母の「共通の倍数（=公倍数）」のなかで「最も小さい数（=最小）」のものを共通の分母にする．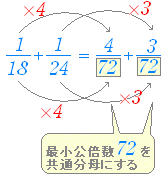

※　このときに登場する「共通の倍数（=公倍数）」の中で「最も小さい数（=最小）」のことを「最小公倍数」という．
18 の倍数は 18, 36, 54, 72, 90, 108, 126, 144, ···
24 の倍数は 24, 48, 72, 96, 120, 144, ···
共通の倍数（=公倍数） 72 , 144 , ··· の中で最小のものは 72
⇒ 最小公倍数は 72

■　間違って「最大公倍数」などと言わないように．公倍数はいくらでも大きいものがあり，最大のものは決まらず「最大公倍数」などという用語は使わない．（=公倍数には最大のものがないから）

■　「最小公倍数」は分数の通分のときだけでなく広く使われる重要なものである．
■ ２つの数の最小公倍数を求めるには，
（Ａ）　小学校のときに習った「割り算（の裏向き）」のやり方で割れるだけ割っていく方法
（Ｂ）　素因数分解を利用する方法
がある．
（Ａ）　割れるだけ割っていく方法で最小公倍数を求めるには
例
2 )18 , 24
3 ) 9 , 12
└ 3 ,_ 4
最小公倍数は2×3×3×4=72
■最小公倍数を求めるときは「割った数」だけでなく，「割った結果」も掛ける．
■　次の計算を参考にして，与えられた２つの数の最大公約数を求めなさい．
［問題１］
2 ) 6 , 10
3 ,_ 5
6 と 10 の最大公約数は

採点する やり直す
［問題２］
3 )30 , 45
5 )10 , 15
2 ,_ 3
30 と 45 の最大公約数は

採点する やり直す
［問題３］
2 )24 , 60
2 )12 , 30
3 ) 6 , 15
2 , 5
24 と 60 の最大公約数は

採点する やり直す
 ■　次の計算を参考にして，与えられた２つの数の最小公倍数を求めなさい．
［問題４］
2 ) 6 , 10
3 ,_ 5
6 と 10 の最小公倍数は

採点する やり直す
［問題５］
3 )30 , 45
5 )10 , 15
2 ,_ 3
30 と 45 の最小公倍数は

採点する やり直す
［問題６］
2 )24 , 60
2 )12 , 30
3 ) 6 , 15
2 , 5
24 と 60 の最小公倍数は

採点する やり直す
（Ｂ）　素因数分解を利用してで最大公約数を求めるには
例1
18=2×32
24=23×3　の形に直す．（素因数分解という）
「最大公約数」は共通の約数（=公約数）のうちで「最大のもの」だから，「共通に入っている素因数」をさがす．
※ 2 は 18 には1個，24 には3個入っているから，共通に入っているのは最大で1個
※ 3 は 18 には2個，24 には1個入っているから，共通に入っているのは最大で1個
最大公約数は2×3=6
例2
100=22__×52
120=23×3×5　の形に直す．（素因数分解という）
「最大公約数」は共通の約数（=公約数）のうちで「最大のもの」だから，「共通に入っている素因数」をさがす．
※ 2 は 100 には2個，120 には3個入っているから，共通に入っているのは最大で2個
※ 3 は 100 には入っていない，120 には1個入っているから，共通に入っているものはない
※ 5 は 100 には2個，120 には1個入っているから，共通に入っているのは1個
最大公約数は22×5=20
【要点】
　最大公約数　⇒　共通の素因数に最小の指数を付ける．
（※　「最大」公約数なのに「最小」の指数なのだ♪　共通に入っているものだから低い方なのだ♪）
（Ｂ）　素因数分解を利用してで最小公倍数を求めるには
例1
18=2×32
24=23×3　の形に直す．（素因数分解という）
「最小公倍数」は共通の倍数（=公倍数）のうちで「最小のもの」だから，両方の倍数になるように「全部の素因数で一番大きな指数をさがす」．
※ 2 は 18 には1個，24 には3個入っているから，両方の倍数になるには3個必要
※ 3 は 18 には2個，24 には1個入っているから，両方の倍数になるには2個必要
最小公倍数は23×32=72
例2
100=22__×52
120=23×3×5　の形に直す．（素因数分解という）
「最小公倍数」は共通の倍数（=公倍数）のうちで「最小のもの」だから，両方の倍数になるように「全部の素因数で一番大きな指数をさがす」．
※ 2 は 100 には2個，120 には3個入っているから，両方の倍数になるには3個必要
※ 3 は 100 には入っていない，120 には1個入っているから，両方の倍数になるには1個必要
※ 5 は 100 には2個，120 には1個入っているから，両方の倍数になるには2個必要
最小公倍数は23×3×52=600
【要点】
　最小公倍数　⇒　全部の素因数に最大の指数を付ける．
（※　「最小」公倍数なのに「最大」の指数なのだ♪　両方の倍数にするには大きい方が必要なのだ♪）
■　次の素因数分解を参考にして，与えられた２つの数の最大公約数を求めなさい．
［問題７］
12=22×3
10=2___×5

12 と 10 の最大公約数は

採点する やり直す
［問題８］
36=22×32
30=2×3×5

36 と 30 の最大公約数は

採点する やり直す
 ■　次の素因数分解を参考にして，与えられた２つの数の最小公倍数を求めなさい．
［問題９］
12=22×3
10=2___×5

12 と 10 の最小公倍数は

採点する やり直す
［問題10］
36=22×32
30=2×3×5

36 と 30 の最小公倍数は

採点する やり直す
○===メニューに戻る
■［個別の頁からの質問に対する回答］[最大公約数,最小公倍数について／17.3.19］
中3　素数·素因数分解　最大公約数·最小公倍数(2) 問題7、問題8、問題9、問題10のHELP 間違っている
＝＞［作者］：連絡ありがとう．めったにない変わったエラーでした･･･指数（肩に付ける小さい数字）が地上に降りていましたので訂正しました．

■このサイト内のGoogle検索■

△このページの先頭に戻る△
【 アンケート送信 】
… このアンケートは教材改善の参考にさせていただきます

■この頁について，良い所，悪い所，間違いの指摘，その他の感想があれば送信してください．
○文章の形をしている感想は全部読ませてもらっています．
○感想の内で，どの問題がどうであったかを正確な文章で伝えていただいた改善要望に対しては，可能な限り対応するようにしています．（※なお，攻撃的な文章になっている場合は，それを公開すると筆者だけでなく読者も読むことになりますので，採用しません．）


質問に対する回答の中学版はこの頁，高校版はこの頁にあります