|
��A��1�g�̕����̌W����������Ă����� �y��A.1�z�@
�@�A��������
�i�l�����j�̉��́C �i���ꌧ2015�N�j
�i���āj (1)+(2) �y��A.2�z�@
�@�A��������
�i�l�����j�������Ȃ����D �i���{2017�N�j
�i���āj (1)−(2) |
�y���A.1�z
�@�A��������
���������
�y���A.2�z
�̉��́C �i���ꌧ2017�N�j
�@�A��������
���������
�����̃y�[�W�̐擪��
�������Ȃ����D �i���{2016�N�j
|
|
��B��1�̕����̌W�����P�ɂȂ��Ă����� �y��B.1�z�@
�@�A��������
�i�l�����j�������Ȃ����B�v�Z�̉ߒ��������Ȃ����D �i�H�c��2015�N�j
�@−�A�~2 �y��B.2�z�@
�@�A��������
�i�l�����j�������Ȃ����B �i��錧2015�N�j
�i���āj
�����̖��ł́C(1)��2�{����
(1)−(2)�~5(1)�~2+(2) |
�y���B.1�z
�@�A��������
���������
�������Ȃ����D �i��ʌ�2016�N�j
�i�l�����j
�y���B.2�z
�i���āj (1)+(2)�~2
�@�A��������
���������
�������Ȃ����D �i�V����2016�N�j
�i���āj (1)+(2)�~3 |
|
�y���B.3�z
�@���̘A���������������Ȃ����D
���������
�i���ꌧ2017�N�j
�i���āj (1)�~3−(2) |
�y���B.4�z
�@�A��������
���������
�������Ȃ����D �i�{�錧2017�N�j
�i���āj (1)�~2−(2) |
|
��C���W�����P��������Ă��Ȃ���� �y��C.1�z�@
�@���̘A���������������D
�i���s�{2017�N�j
(1)�~3−(2)�~4�ɂ����  �i���āj (1)�~2+(2)�~3 �y��C.2�z�@
�@�A��������
�i�l�����j�������Ȃ����B �i���m��2017�N�j
�܂��C�ڍ����Č`�𐮂��Ă���l���܂��D
 �i���āj (1)�~2+(2)�~3 |
�y���C.1�z
�@���̘A���������������Ȃ����D
���������
�i�啪��2015�N�j
�i���āj (1)−(2)�~2
�@�A��������
���������
�������D �i�����s2015�N�j
������ȕ����̓����ɂȂ��Ă��܂�����C�����Ă��邩�ǂ����S�z�ɂȂ邪�C���Z���Đ��藧���Ă���C�����ɂ���D�i�i�w�d�_�w���Z�炵���̂ŁC����炵���j ������C���藧�� �i���āj (1)�~5−(2)�~9 |
|
��D��y=�܂���x=�̎��������� �y��D.1�z�@
�@�A��������
�������Ȃ����D �i���쌧2015�N�j
���̖��̂悤�ɁC
�i�l�����j�i���āj (1)��(2)�ɑ�������m(2)�� �y��D.2�z�@
�@�A��������
�������Ȃ����B �i�H�c��2016�N�j
���̖��̂悤�ɁC
�i�l�����j�i���āj (1)��(2)�ɑ�������m(2)�� |
�y���D.1�z
�@�A��������
���������
�̉��́C �i���ꌧ2016�N�j
���̖��̂悤�ɁC
�i�l�����j�i���āj (2)��(1)�ɑ������ �m(1)��
�@�A��������
���������
�������D �i������2016�N�j
���̖��̂悤�ɁC
�i�l�����j�i���āj (2)��(1)�ɑ�������m(1)��
���Ƃł�
|
|
��E�������C�����̌W���������� �y��E.1�z�@
�@���̘A���������������Ȃ����D
�i���ꌧ2016�N�j
(2)���̂悤�ɏ�����1�ʂ܂ł�0.2��0.1�C������2�ʂ܂ł�0.15������Ƃ��C�����S���𐮐��W���ɒ����ɂ́C100���|���܂�
�i�l�����j�i���āj (2)�̗��ӂ�100�{���Đ����W���ɒ��� �y��E.2�z�@
�@�A��������
�������D �i�����s2015�N�j
�����W���ɂȂ��Ă���Ƃ��́C���ӂ̍ŏ����{�����|���ĕ�����D�i�ŏ����{����������Ȃ��Ƃ��́C����̐�����S�������Ă���C��Ŋ���邾������悢�j
�i�l�����j�i���āj (1)�̗��ӂ�6�{���Đ����W���ɒ���
�ςȓ���������C�ԈႢ���ƐS�z�ɂȂ邪�C���Z���č����Ă���C���̂܂܉�����D
(1’)−(2’)�~2 |
�y���E.1�z
�@�A��������
���������
�������D �i�����s2015�N�j
�����W���������W�������{�����Đ����W���ɒ����ĉ����܂�
�i�l�����j�i���āj (1)�̗��ӂ�6�{���Đ����W���ɒ���
�@�A��������
���������
�������D �i�����s2017�N�j
�����W���������W�������{�����Đ����W���ɒ����ĉ����܂�
�i�l�����j�i���āj (1)�̗��ӂ�6�{���Đ����W���ɒ��� |
|
��F���A�Ȃ�^�i �y��F.1�z�@
�@������
�i�k�C��2015�N�j
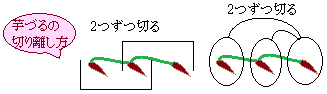
�܂���
�̂悤�ɁC(1)(2)�ł� 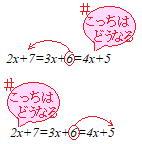 �y�藣�����R�z
�y�藣�����R�z�@�E�̂悤�ɁC�C�R�[�����Q�t�����܂܂ɂ���ƁC���܂Ŏ��R�Ɏg���Ă����u�ڍ��v�̂悤�ȕό`���C���܂��ł��Ȃ�����C�藣���Đg�y�ɂ���̂ł��D ���R�l���Ɓu���߂�v����ł���←�l��b�����I
�܂���
���̖��ł�(3)(4)�̐藣�����̕����y��������܂���D[(1)(2)�̂悤�ɐ藣�����ꍇ�C����ɕό`����K�v������܂��D]
�i���āj(3)�~3−(4)�~5 |
�y���F.1�z
�@�A��������
���������
�i�{�錧2015�N�j
�i�l�����j
�����̃y�[�W�̐擪��
�܂���
���̖���(3)(4)�̐藣�����̕����y�ł��傤
�i���āj(3)�~2+(4) |
|
��G��������W��a,b�����߂��� �y��G.1�z�@ �̉��� �i������2015�N�j
�@
�i���āj�@���̂Ƃ��ł���̂́C �@ (1)+(2) |
�y���G.1�z
�̉����C �i���ꌧ2015�N�j
|
|
�y���G.2�z
�̉��� �i�����s2016�N�j
|