|
■方程式の文章題(食塩水の濃度)
問題1-1ある町では人口の6%が中学生であった.この町に新たに100人の転入者があったが中学生は含まれておらず,その結果,中学生は人口の4%になった.
(1)はじめの人口をx人として,その6%である中学生の人数を左辺とし,後の人口の4%である中学生の人数を右辺として,それらが等しいことをxの方程式で表すと,次のうちどの式になりますか. Help 0.06x=0.04x+100 0.06x=0.04x−100 0.06x=0.04(x+100) 0.06x=0.04(x−100) =+100 =−100 = = |
xを使って中学生の数を表します.
(1)
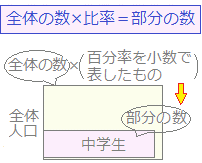 後は人口(x+100)人の4% ⇒ 0.04(x+100) 中学生の数は,はじめと後で等しいから 0.06x=0.04(x+100) (2) 方程式の両辺に100を掛けて,小数を整数に直すと 6x=4(x+100) 6x=4x+400 2x=400 x=200 |
|
問題1-2ある容器には濃度6%の食塩水が入っている.この容器に水100gを加えたら,食塩水の濃度は4%になった.
(1)はじめ食塩水がxgあったとして,その6%である食塩の重さを左辺とし,後の食塩水の重さの4%である食塩の重さを右辺として,食塩の重さが変わらない(それらが等しい)ことをxの方程式で表すと,次のうちどの式になりますか. Help 0.06x=0.04(x−100) 0.06x=0.04(x+100) 0.06x=0.04x−100 0.06x=0.04x+100 = = =−100 =+100 |
※「食塩水の濃度」と聞いて苦手意識を持ったあなたへ!⇒この問題は,そのあなたのための問題です.
上の問題の中学生/人口の関係を,この問題では食塩/食塩水に置き換えて,食塩の重さを式で表すと,同じ方法で解けます.
xを使って食塩の重さを表します.
(1)
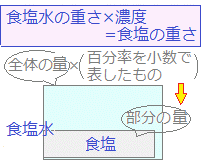 ⇒ 0.06x 後の食塩水の重さ(x+100)gの4% ⇒ 0.04(x+100) 食塩の重さは,はじめと後で等しい(水しか入れていないので食塩の重さは増えていない)から 0.06x=0.04(x+100) (2) 方程式の両辺に100を掛けて,小数を整数に直すと 6x=4(x+100) 6x=4x+400 2x=400 x=200 |
|
問題1-3濃度10%の食塩水に水200gを加えたら,6%の食塩水になった.
(1)はじめ食塩水がxgあったとして,xの方程式を作ると,次のうちどの式になりますか. Help = = =−100 =+100 0.1x=0.06(x−200) 0.1x=0.06(x+200) 0.1x=0.06x−200 0.1x=0.06x+200 |
xを使って食塩の重さを表します.
(1)はじめ食塩水がxgあったとするとその10%が食塩の重さになります. ⇒ 0.1x 後の食塩水の重さ(x+200)gの6% ⇒ 0.06(x+200) 食塩の重さは,はじめと後で等しい(水しか入れていないので食塩の重さは増えていない)から 0.1x=0.06(x+200) (2) 方程式の両辺に100を掛けて,小数を整数に直すと 10x=6(x+200) 10x=6x+1200 4x=1200 x=300 |
|
問題1-4濃度6%の食塩水100gに水を何g加えたら,5%の食塩水になるか,方程式を使って求めたい.
(1)水をxg加えるとして方程式を作ると,次のうちどの式になりますか. Help 0.06x=0.05(100+x) 0.06×100=0.05(100+x) 0.06(100+x)=0.05x 0.06×100+x=0.05x 0.06x+100=0.05x 0.06x=0.05x+100 |
xを使って食塩の重さを表します.
(1)はじめ6%の食塩水が100gあったのだから,食塩の重さは ⇒ 0.06×100 後の食塩水の重さ(100+x)gの5%は食塩だから ⇒ 0.05(100+x) 食塩の重さは,はじめと後で等しい(水しか入れていないので食塩の重さは増えていない)から 0.06×100=0.05(100+x) (2) 方程式の両辺に100を掛けて,小数を整数に直すと 0.06×100=0.05(100+x) 600=5(100+x) 600=500+5x x=20 |
|
問題2-1はじめに列車に乗っていた乗客のうち中学生の割合は20%だった.ある駅では誰も降りずに40人の乗客が乗り,そのうちの25%は中学生だった.最後に中学生の割合が22%になったとき,はじめに列車に乗っていた乗客の数を求めたい.
(1)はじめの乗客をx人として,中学生の人数について成り立つ関係
(初めの乗客の20%)+(駅から乗った乗客の25%)
を方程式で表すと,次のうちどの式になりますか.=(最後の乗客の22%) Help 0.2x+0.25×40=0.22x 0.2x+40=0.22(x+40) 0.2x+0.25=0.22(x+40) 0.2x+0.25×40=0.22(x+40) |
xを使って中学生の数を表します.
(1)はじめの中学生の数はx人の20% ⇒ 0.2x 駅から乗った中学生は40人の25% ⇒ 0.25×40 最後の中学生は(x+40)人の22% ⇒ 0.22(x+40) 方程式は 0.2x+0.25×40=0.22(x+40) (2) 方程式の両辺に100を掛けて,小数を整数に直すと 20x+25×40=22(x+40) 20x+1000=22x+880 −2x=−120 x=60 |
|
問題2-2ある容器には濃度5%の食塩水が入っている.この容器に10%の食塩水300gを加えたら,食塩水の濃度は7%になった.
(1)はじめ食塩水がxgあったとして,食塩の重さについて成り立つ関係
(はじめの食塩水に含まれていた食塩の重さ)
を方程式で表すと,次のうちどの式になりますか.+ (加えた食塩水中の食塩の重さ) = (できた食塩水中の食塩の重さ) Help 0.05x+10=0.07(x+300) 0.05x+0.1×300=0.07×300 0.05x+0.1×300=0.07(x+300) 0.06x+0.1×300=0.07x |
xを使って食塩の重さを表します.
(1)
 はじめの食塩水の5% ⇒ 0.05x 加えた食塩水の10% ⇒ 0.1×300 できた食塩水の7% ⇒ 0.07(x+300) 0.05x+0.1×300=0.07(x+300) (2) 方程式の両辺に100を掛けて,小数を整数に直すと 5x+10×300=7(x+300) 5x+3000=7x+2100 −2x=−900 x=450 |
|
問題2-33%の食塩水に9%の食塩水30gを加えたら,5%の食塩水になった.
(1)はじめ食塩水がxgあったとして,xの方程式を作ると,次のうちどの式になりますか. Help 0.03x+0.09×30=0.05×30 0.03x+0.09×30=0.05(x+30) 0.03x+30=0.05x 0.03x+9=0.05(x+30) |
xを使って食塩の重さを表します.
(1) はじめの食塩水の3% ⇒ 0.03x 加えた食塩水の9% ⇒ 0.09×30 できた食塩水の5% ⇒ 0.05(x+30) 0.03x+0.09×30=0.05(x+30) (2) 方程式の両辺に100を掛けて,小数を整数に直すと 3x+9×30=5(x+30) 3x+270=5x+150 −2x=−120 x=60 |
|
問題2-412%の食塩水300gに濃度がよく分からない食塩水200gを加えたら,14%の食塩水になった.加えた食塩水の濃度を方程式を使って求めたい.
(1)加えた食塩水の濃度をx%として方程式を作ると,次のうちどの式になりますか. Help 0.12×300+0.01x×200=0.14×500 0.12×300+0.01x×200=0.14(300+x) 0.12×300+x×200=0.14×500 0.12×300+x×200=0.14(300+x) |
3%の食塩水200g⇒食塩の重さは0.03×200g
(1)5%の食塩水200g⇒食塩の重さは0.05×200g x%の食塩水200g⇒食塩の重さは0.01x×200g 食塩の重さは はじめの食塩水の12% ⇒ 0.12×300 加えた食塩水のx% ⇒ 0.01x×200 できた食塩水の14% ⇒ 0.14×500 0.12×300+0.01x×200=0.14×500 (2) 方程式の両辺に100を掛けて,小数を整数に直すと 12×300+200x=14×500 3600+200x=7000 200x=3400 x=17 |