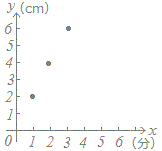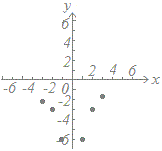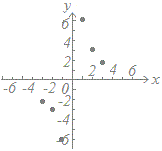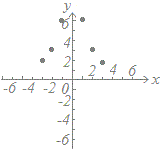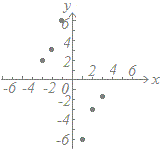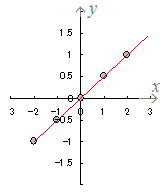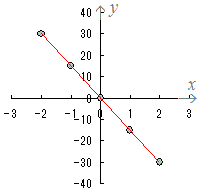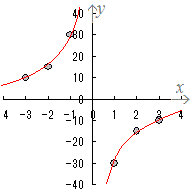== データとグラフ ==
■グラフの書き方
○ 右の表1は空の水そうに水道の水を入れていったときの、はじめからの時間(分)とたまった水の深さ(cm)を表にしたものとします。
この表をグラフに表すとき、はじめからの時間(分)を横(x)に、たまった水の深さ(cm)を縦(y)にとってグラフで表すには
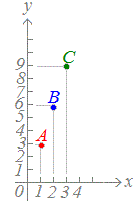
- 1分後に3(cm)までたまったことは、x=1 , y=3となる点(1 , 3)で表されます。(図の点A)
- 2分後に6(cm)までたまったことは、x=2 , y=6となる点(2 , 6)で表されます。(図の点B)
- 3分後に9(cm)までたまったことは、x=3 , y=9となる点(3 , 9)で表されます。(図の点C)
○ 観察・実験結果の表を点のグラフで表すには、表の上の段の数字を横( x)に、表の下の段の数字を縦( y)とする座標 (x , y)を考えて点で表します。
縦に並んだ1組が x座標と y座標です。
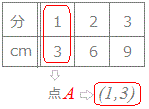
この表にはデータが3組ありますので、点が3個できることになります。
|
表1
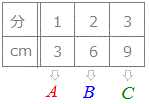 図1
図1
|
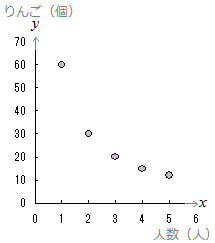
○ 次の表2は60(個)のりんごを何人かで分けるときの人数(人)と1人がもらえるりんご(個)を表したものです。
表2
| 人数(人) |
1 |
2 |
3 |
4 |
5 |
| りんご(個) |
60 |
30 |
20 |
15 |
12 |
このような表をグラフに表すとき、x , yを1ずつ目盛りを付けると縦yに非常に大きな数字が登場しますので、「縦に非常に長い」「分かりにくい」グラフになります。そのため、
- 縦yと横xの目盛りの幅は変えてもよいことにします。(ただし、中学生が作るグラフでは縦横のそれぞれは等間隔になっていることが重要です。)
- 縦の目盛りを1,2,3,···などと細かく付けていくと、グラフを書き始めるまでに長時間かかってしまい、グラフも「見にくく」「分かりにくい」ものになりますので、縦の目盛りは大きく5,10,15,···とか10,20,30,···の所だけ書くようにします。
表2をグラフで表すと右の図2のようになります。
|
図2
|
|
.
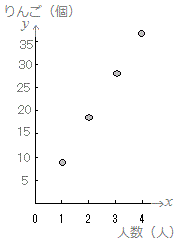
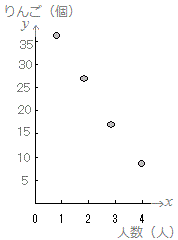
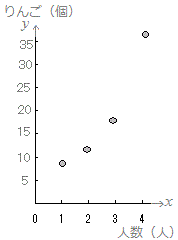
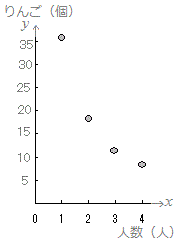
≪問題1≫ 次の各表において上の段の数字を横(x)に、表の下の段の数字を縦(y)として点で表したグラフを選んでください。
(2)
| 人数(人) |
1 |
2 |
3 |
4 |
| りんご(個) |
36 |
18 |
12 |
9 |
(3)
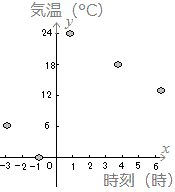
| 時刻(時) |
0 |
6 |
12 |
18 |
24 |
| 気温(°C) |
−1 |
−3 |
6 |
4 |
1 |
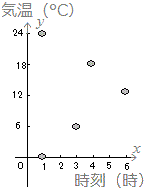
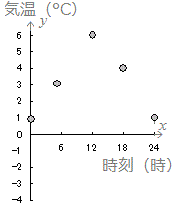
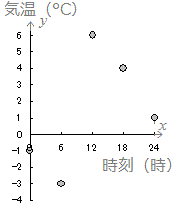
(5)
| x |
−3 |
−2 |
−1 |
0 |
1 |
2 |
3 |
| y |
2 |
3 |
6 |
× |
−6 |
−3 |
−2 |
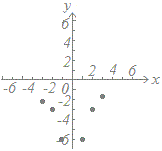
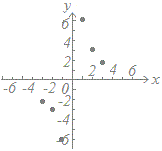
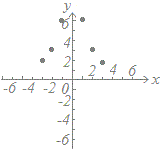
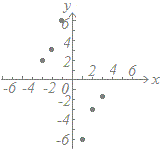
|
■直線や曲線の利用
観測したデータが少ない場合でも、それらを「なめらかな」(なるべくデコボコが少ないような)直線や曲線で結ぶと
- xとyの関係が分かりやすくなります。
- 直接観測していないデータについても予想することができます。
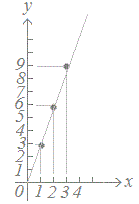
例えば、右の表3をグラフにして、なめらかな線で結ぶと図3のようになり、y=3xの関係があると予想できます。これにより、x=4のときy=12になると予想できます。
|
表3
図3
|
≪問題2≫ 各表とグラフから、指定されたxの値のときのyの値を予想してください。
(1)
| x |
−2 |
−1 |
0 |
1 |
2 |
| y |
−1 |
−0.5 |
0 |
0.5 |
1 |
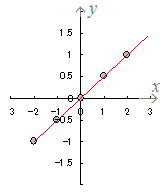
|
x=3のとき
yは幾らになりますか
1.5
2
2.5
3
|
.
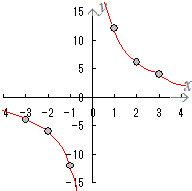
(2)
| x |
−3 |
−2 |
−1 |
0 |
1 |
2 |
3 |
| y |
−4 |
−6 |
−12 |
× |
12 |
6 |
4 |
|
x=4のとき
yは幾らになりますか
1
2
3
6
|
|
(3)
| x |
−2 |
−1 |
0 |
1 |
2 |
| y |
30 |
15 |
0 |
−15 |
−30 |
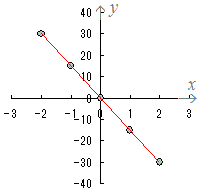
|
x=−0.5のとき
yは幾らになりますか
−10
−7.5
7.5
10
|
(4)
| x |
−3 |
−2 |
−1 |
0 |
1 |
2 |
3 |
| y |
10 |
15 |
30 |
× |
−30 |
−15 |
−10 |
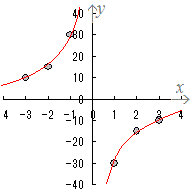
|
x=5のとき
yは幾らになりますか
5
−5
6
−6
|
|