|
≪解説≫ ○ 割合の表し方 割合を表す1つの方法として、百分率(パーセント)があります(世界共通です)。 百分率(パーセント)は0.01を単位(1パーセント,1%)として表すものです。
例
・ 0.03=3%0.12=12%0.8=80% (1) 基準の量と百分率が与えられたときに、比較しているものの量を求めるには:
例
・50(g)の1%は、50(g)×0.01=0.5(g) ・100(人)の30%は、100(人)×0.3=30(人) ⇒ このように、基準の量と百分率が、何の何パーセントという形で与えられたとき、
(何の何パーセント→量)「パーセントから量を求める問題」では
の2段階で求めることができます。
(1) パーセントを小数に直す:1% → 0.01 など (2) 基準の量に小数を掛ける:50×0.01=0.5 など 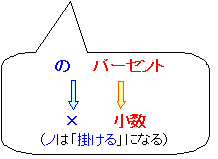
例題1
80(g)の15%は、何(g)ですか (解答) 80×0.15=12(g)
例題2
500(人)の7%は、何(人)ですか (解答) 500×0.07=35(人)
例題3
仕入れ値200(円)の商品を仕入れ値の10%増しの定価を付けて売るとき、売値は幾らになりますか。 (解答) 10%増しだから、増分は200×0.1=20(円) 200+20=220(円)・・・(答) (別解) 10%増しだから、仕入れ値の110%=1.1倍になる 200×1.1=220(円)
例題4
定価150(円)の商品を10%引きで売るとき、売値は幾らになりますか。 (解答) 10%引きだから、値引きは150×0.1=15(円) 150−15=135(円)・・・(答) (別解) 10%引きだから、定価の90%=0.9倍になる 150×0.9=135(円) |
(2) 割合(パーセント)を求めるには:
例
⇒ このように、
5(g)は50(g)の何パーセントか? (1) 基準の量で割り算をして比率を求める:5÷50=0.1
これは、「分母が基準の量」となる分数と同じです:
(2) 比率を百分率(パーセント)で表す:0.1=10%
=0.1
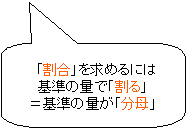
割合(パーセント)を求める問題では
の2段階で求めることができます。
(1) 基準の量で割って割合を比率を小数で求める: (比較する量)÷(基準の量)
分数で書けば
(2) 小数をパーセントに直す
例題1
ある選挙で候補者Aには、450(票)の投票がありました。これは、投票総数3000(人)の何(%)に当たりますか。 (解答) 450÷3000=0.15 0.15=15(%)
例題2
ある家の今月の電気代は、5000(円)で、先月の電気代は4000(円)でした。今月の電気代は先月の電気代の何%ですか。 (解答) 5000÷4000=1.25 1.25=125(%) ※先月の電気代が基準なので、先月の電気代で割る。 (もし、「先月の電気代は今月の電気代の何%ですか」という問題ならば、4000÷5000=0.8=80%と答えます。) (*) 基準が隠されているとき
例 ・ある大学では、定員の45(%)の90(人)を推薦入試で合格とした。定員は何人ですか。 (定員)×0.45=90 だから (定員)=90÷0.45=200(人) ⇒ このように、
(比較する量)÷(基準の量)=(割合) ・・・小数で表したもの だから、どれか1つが分からないときは、この式から求めることができます。
上の(2)で扱ったもの・・・割合=
この(*)で扱ったもの・・・基準の量=
|
|
≪問題≫ 次の各々について、正しいものを右の選択肢から選んでください。
(1)400(g)の5%は → 200(g), 80(g), 20(g), 8(g), 2(g)
5%を小数に直すと0.05になる. 400×0.05=20
(2)180(人)の60%は → 172(人), 150(人), 108(人), 30(人), 3(人)
60%を小数に直すと0.6になる. 180×0.6=108
(3)640(m2)の25%は → 820(m2), 480(m2), 256(m2), 160(m2), 48(m2)
25%を小数に直すと0.25になる. 640×0.25=160
(4)500(円)で仕入れた品物に仕入れ値の40%の利益を見込んで(予定して,当てにして)定価を付けると、定価は何円になりますか → 800(円), 700(円), 625(円), 200(円), 125(円)
40%を小数に直すと0.4になる. 500×0.4=200(円)が利益だから、定価は700(円)
(5)定価500(円)の品物を定価の20%引きで売ると、売値は何円になりますか → 480(円), 375(円), 400(円), 250(円), 100(円)
20%を小数に直すと0.2になる. 500×0.2=100(円)だけ引くから、売値は400(円)
(6)96(kg)は480(kg)の何% → 80(%), 50(%), 20(%), 5(%), 2(%)
480が基準の量なので、480で割ります. 96÷480=0.2だから、20(%)
(7)50(リットル)は125(リットル)の何% → 40(%), 25(%), 4(%), 2.5(%), 0.4(%)
125が基準の量なので、125で割ります. 50÷125=0.4だから、40(%)
(8)50(円)は40(円)の何% → 200(%), 125(%), 80(%), 12(%), 8(%)
40が基準の量なので、40で割ります. 50÷40=1.25だから、125(%)(※基準の量よりも比較する量が多いときは100%よりも大きくなります。)
(9)ある学校の女子生徒数は90(人)で、これは全校生徒数の60(%)に当たります。全校生徒数は → 540(人), 180(人), 150(人), 54(人), 15(人)
全校生徒数×0.6=90だから、全校生徒数=90÷0.6=150(人)
(10)ある学校の生徒について自転車通学者を調べたところ全校生徒の40(%)、80(人)が自転車通学だった。全校生徒数は → 800(人), 400(人), 200(人), 160(人), 32(人)
全校生徒数×0.4=80だから、全校生徒数=80÷0.4=200(人)
|
|