|
← PC�p�͕ʕ�
�y���̕ł̖ڕW�z
�@�P�����̃O���t�����āC����������������悤�ɂ���D I�����̃O���t����u�ؕ��v�Ɓu�X���v��ǂݎ���悤�ɂ���D II�����̃O���t�����P�����̕�����������悤�ɂ���D III�X���������ɂȂ�Ƃ��ł��C�����̃O���t����P�����̕�����������悤�ɂ���D |
|
�������̕������i�P�����̕������j
--�}�P--
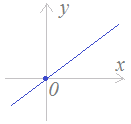
�����̕�������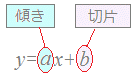 �@�̌`�ŏ������Ƃ� (1)�萔��b�́u�ؕ��v�ƌĂ�܂��D
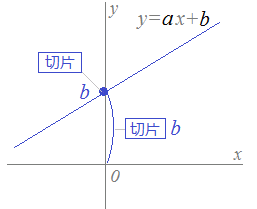
•�ؕ�b�́C���̐}�Q�̂悤��y���Ƃ̌�_�i��y���W�j��\���Ă��܂��D
•b�����̐��ɂȂ�Ƃ��́Cb�͌��_����y���Ƃ̌�_�܂ł̒����ɂȂ�܂��D
--�}�Q--�@��ؕЁ�
 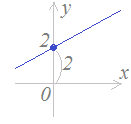 �y��P�z �y��P�z�E�̒����̐ؕЂ�2�ł��D �����̕�������y=ax+2�̌`�ɂȂ�܂��D 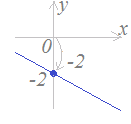 �y��Q�z �y��Q�z�E�̒����̐ؕЂ�−2�ł��D �����̕�������y=ax−2�̌`�ɂȂ�܂��D
•y���ƌ��_(0, 0)�Ō�����Ă���Ƃ��C�ؕЂ̒l��0�ɂȂ�܂��D
 �y��R�z �y��R�z�@�E�̒����̐ؕЂ�0�ł��D �����̕�������y=ax+0�̌`�ɂȂ�܂��D �@���̂Ƃ��́C�P��y=ax�̌`�ŕ\���܂��D �@���̂悤�Ȓ萔�����O�i�Ȃ��j�̃O���t�́C���w�Z�P�N���̎��ɏK�������̃O���t�ɂȂ�܂��D (2)x�̌W��a�́u�X���v�ƌĂ�܂��D
•�X��a�́C�������}�ȌX�ɂȂ��Ă��邩�C�ɂ₩�ȌX�ɂȂ��Ă��邩���p�x�ł͂Ȃ��u�P�̐����v�ŕ\�������̂ł��D
•�X��a�́Cx�̐��̌����ɂP�ڐ���i�Ƃ���y�̌����Ɋ��i�ނ����u�����t���̐����Łv�\�������̂ł��D
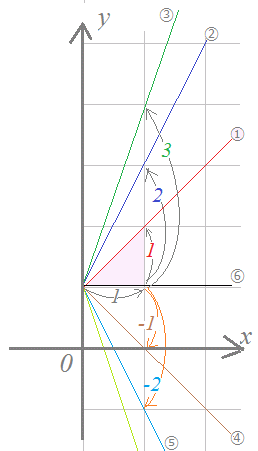
�Ⴆ�Ύ��̐}�R�ŁC
�@�̃O���t��x�̐��̌����ɂP�ڐ���i�Ƃ���y�̌�����1�����i��ł���̂ŁC�����@�̌X����1�ł��D�ia=1�j
--�}�R--�@��X����
 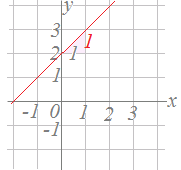 �y��S�z �y��S�z�@�E�̒����̌X����1�ł��D �����̕�������y=1x+b=x+b�̌`�ɂȂ�܂��D �@�ؕ�b=2���ǂݎ��ƁC���ǁC�����̕�������y=x+2�ł��邱�Ƃ�������܂��D
�A�̃O���t��x�̐��̌����ɂP�ڐ���i�Ƃ���y�̌�����2�����i��ł���̂ŁC�����A�̌X����2�ł��D
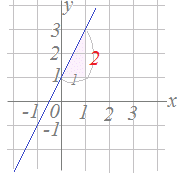 �y��T�z �y��T�z�@�E�̒����̌X����2�ł��ia=2�j�D �����̕�������y=2x+b�̌`�ɂȂ�܂��D �@�ؕ�b=1���ǂݎ��ƁC���ǁC�����̕�������y=2x+1�ł��邱�Ƃ�������܂��D
�B�̃O���t��x�̐��̌����ɂP�ڐ���i�Ƃ���y�̌�����3�����i��ł���̂ŁC�����B�̌X����3�ł��D
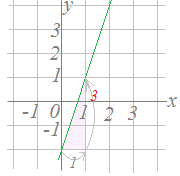 �y��U�z �y��U�z�@�E�̒����̌X����3�ł��D�ia=3�j �����̕�������y=3x+b�̌`�ɂȂ�܂��D �@�ؕ�b=−2���ǂݎ��ƁC���ǁC�����̕�������y=3x−2�ł��邱�Ƃ�������܂��D |
|
��̐}�R�ŁC�C�̃O���t��x�̐��̌����ɂP�ڐ���i�Ƃ���y�̌�����−1�����i��ł���̂ŁC�����C�̌X����−1�ł��D
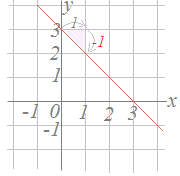 �y��V�z �y��V�z�@�E�̒����̌X����−1�ł��D�ia=−1�j �����̕�������y=−1x+b=−x+b�̌`�ɂȂ�܂��D �@�ؕ�3���ǂݎ��ƁC���ǁC�����̕�������y=−x+3�ł��邱�Ƃ�������܂��D
��̐}�R�ŁC�D�̃O���t��x�̐��̌����ɂP�ڐ���i�Ƃ���y�̌�����−2�����i��ł���̂ŁC�����D�̌X����−2�ł��D
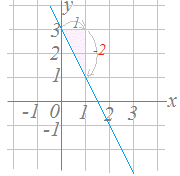 �y��W�z �y��W�z�@�E�̒����̌X����−2�ł��D�ia=−2�j �����̕�������y=−2x+b�̌`�ɂȂ�܂��D �@�ؕ�3���ǂݎ��ƁC���ǁC�����̕�������y=−2x+3�ł��邱�Ƃ�������܂��D
��̐}�R�ŁC�E�̃O���t��x�̐��̌����ɂP�ڐ���i�Ƃ���y�̌����Ɂu�S���i��ł��܂���v�D���̒����E�̌X����0�ŕ\���܂��D
���̂悤�ɁCx���ɕ��s�Ȓ����̌X����0�ł��D 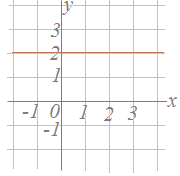 �y��X�z �y��X�z�@�E�̒����̌X����0�ł��D�ia=0�j �����̕�������y=0x+b=b�̌`�ɂȂ�܂��D �@�ؕ�2���ǂݎ��ƁC���ǁC�����̕�������y=2�ł��邱�Ƃ�������܂��D |
|
���P���̂P�����̃O���t�ɂ��āC�X���ƐؕЂ����߂Ă��������D
(�e�X�C���̑I��������I��ł��������D�j ���͂W�肠��܂��D �Ԉ�����Ƃ���Help������ ���̖����o���ɂ�Next������ �O���t[1 / 8]Next 


|
|
�y�ؕЁz �y�X���z |
|
���Q���̂P�����̕����������߂Ă��������D
(���̑I��������I��ł��������D�j �O���t[1 / 10]Next 


|
|
�y�������z |
�������ɂȂ�Ƃ��̌X���̓ǂݕ�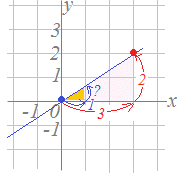 �@�E�̂悤�Ȓ������X����ǂݎ�肽���Ƃ��Cx��1�������������Ƃ���y�̑�����ǂݎ�낤�Ƃ���ƁC�����i�����j�ɂȂ��Ă��܂��Đ��m�ɓǂݎ��܂���D
�@�E�̂悤�Ȓ������X����ǂݎ�肽���Ƃ��Cx��1�������������Ƃ���y�̑�����ǂݎ�낤�Ƃ���ƁC�����i�����j�ɂȂ��Ă��܂��Đ��m�ɓǂݎ��܂���D�@���̂悤�ȏꍇ�C�u���̊W�v���v���o���ƁC�E�}�ʼn��F�̒��p�O�p�`�́u���̒����F�c�̒����v�͓��F�̒��p�O�p�`�́u���̒����F�c�̒����v�Ɠ����ɂȂ��Ă��܂��D �@�����ŁC���̂悤�ȏꍇ�ɂ͏c�̒��������߂₷�����܂Ői���
�X����
�ɂ���Čv�Z���邱�Ƃ��ł��܂��D�@�u�K�i�̊G��`���Ƃ��ɁC�����͎g���₷���悤�Ɍ��߂Ă��悢�v�Ƃ������Ƃł��D�i����傫������Əc���傫���Ȃ�̂ŁC�����Ƃ��Ă͓������̂ɂȂ�܂��D�j �@���̐}�ł́C
�X����
�ɂȂ�܂��D |
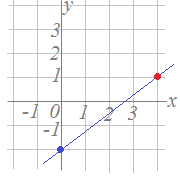 ��10
��10�@�E�̂悤�Ȓ����̕�������ǂݎ�肽���Ƃ��C ���@�̓_��y���W����ؕЂ�−2�ł��D ���@���ɁC�X�������߂�Ƃ��ɁCx��1�������������Ƃ���y�̑�����ǂݎ�낤�Ƃ���ƁC�����i�����j�ɂȂ��Ă��܂��Đ��m�ɓǂݎ��܂���D �@�����ŁC�E�ɐi���x���W�Cy���W�̗����Ƃ������ł���悤�ȓ_��T���ƁC�ԂŎ������_�܂ʼnE��4�C���3�i�߂悢���Ƃ�������܂��D �@�X�����ɂȂ�܂��D ���@������g�ݍ��킹��ƁC�����̕����������܂�܂��D �@�����̕������@�F�@y=x−2 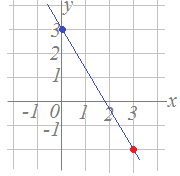 ��11
��11�@�E�̂悤�Ȓ����̕�������ǂݎ�肽���Ƃ��C ���@�̓_��y���W����ؕЂ�3�ł��D ���@���ɁC�X�������߂�Ƃ��ɁCx��1�������������Ƃ���y�̑�����ǂݎ�낤�Ƃ���ƁC�����i�����j�ɂȂ��Ă��܂��Đ��m�ɓǂݎ��܂���D �@�����ŁC�E�ɐi���x���W�Cy���W�̗����Ƃ������ł���悤�ȓ_��T���ƁC�ԂŎ������_�܂ʼnE��3�C���−5�i����5�j�i�߂悢���Ƃ�������܂��D �@�X����−�ɂȂ�܂��D ���@������g�ݍ��킹��ƁC�����̕����������܂�܂��D �@�����̕������@�F�@y=−x+3 |
|
���R���̂P�����̕����������߂Ă��������D
(���̑I��������I��ł��������D�j �O���t[1 / 10]Next 


|
|
�y�������z |