|
《三平方の定理》 《問題１》 半径ｒの円において中心から弦ＡＢまでの距離がｘであるとき，弦ＡＢの長さは次のような直角三角形を利用して求めることができます．ただし，ｙの２倍が弦ＡＢの長さとなります． このとき，弦ＡＢの長さをｒとｘを用いて表わすと，次のうちどの式になりますか．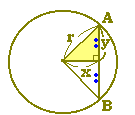      
《問題２》 半径３の円の中心から６離れた点からこの円に接線を引いたとき，この接線の長さを求めなさい． （通常，接線は接点までの「線分」と考えますので，長さは無限ではありません．）
     ヒント
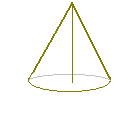
《問題３》 底面の半径が３，母線の長さが６であるような円錐の高さを求めなさい．
《問題４》 半径の長さが各々３と２である円において，中心間の距離が７であるとき，これら２円の共通内接線の長さを求めなさい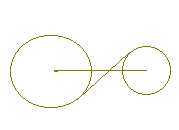．     ヒント
《問題５》 半径３と半径２の円が外接しているとき，それら２円の共通外接線の長さを求めなさい．  
《問題６》 縦，横，高さが各々４，５，３である直方体の対角線の長さを求めなさい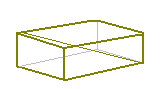．     ヒント
《問題７》（普通） 次の図において△ABCは∠A=90°の直角三角形で，S1 , S2 , S3は各々AB, AC, BCを直径とする半円の面積とする．このとき，S1 , S2 , S3の関係として正しいものを次の中から選べ．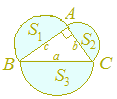 
S3<S1+S2
S3=S1+S2
S3>S1+S2
ヒントS3=π()2=πa2, S1=π()2=πc2, S2=π()2=πb2で，三平方の定理によりa2=b2+c2が成り立つから，S3=S1+S2 《問題８》（やさしい） 次の図において△ABCは∠A=90°の直角三角形で，S1 , S2 , S3は各々△ABCの外接円と辺AB, AC, BCとで囲まれた図形の面積とする．このとき，S1 , S2 , S3の関係として正しいものを次の中から選べ．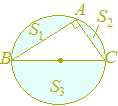 
S3<S1+S2
S3=S1+S2
S3>S1+S2
ヒント△ABCの面積をSとおくと，S3=S1+S2+SだからS3>S1+S2 《問題９》（むずかしい） 次の図において△ABCは∠A=90°の直角三角形で，S1 , S2 , S3は各々ABを直径とする半円のうちで△ABCの外接円の外側にある部分の面積，ACを直径とする半円のうちで△ABCの外接円の外側にある部分の面積，△ABCの面積とする．このとき，S1 , S2 , S3の関係として正しいものを次の中から選べ．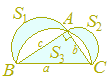 
S3<S1+S2
S3=S1+S2
S3>S1+S2
ヒント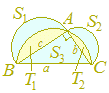
≪問題７≫の結果を使うと，右の図において(S1+T1 )+(S2+T2 )=(S3+T1+T2 )が成り立つから，S3=S1+S2 |
