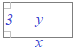.

== 比例 ==

○　xが増えたらyも増える関係になっているものには，いろいろな種類があります．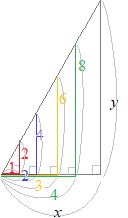
【例１】
　右図のように１つの斜辺を縦横に切ってできる直角三角形の縦の長さyと横の長さxの関係
x01234…
y02468…

xが増えるとyも増え，
y=2x
の関係になる．

この例のように，１つの定数a（上の例ではa=2）を使って
y=ax
の形に書けるときyはxに比例するといいます．
◎中学校１年生の数学では比例の関係を学びます．
【例２】
　兄が弟よりも2歳年上で，兄の年齢をy，弟の年齢をxとすると
x01234…
y23456…

xが増えるとyも増え，
y=x+2
の関係になる．
▼この例のように，yを表す式でxに対して定数の足し算や引き算が付いているものは「１次関数」と呼ばれ中学校２年生の数学で習います．
（１次関数の例）
y=2x+3
y=3x−4
右上に続く↑
→続き
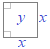
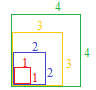
【例３】
　右図のような１辺の長さがxである正方形の面積をyとすると
x…1234…
y…12223242…

xが増えるとyも増え，
y=x2
の関係になる．

▼この例のように，yがxの２次式で表されるような場合「２次関数」と呼ばれ，中学校３年生や高校１年生の数学で学びます．
（中学３年生で習う２次関数の例）
y=3x2
y=−2x2
（高校１年生で習う２次関数の例）
y=x2+3x+4
y=2x2−3x+5
【要約】
◎　定数a（ただしa≠0）を使って
y=ax
に形に書けるとき，yはxに比例するといい，aを比例定数という．
▼　定数a, b（ただしa≠0）を使って
y=ax+b
に形に書けるとき，yはxの１次関数であるという．
▼　定数a, b, c（ただしa≠0）を使って
y=ax2+bx+c
に形に書けるとき，yはxの２次関数であるという．

【例題１】
　次の関係があるときyをxで表す式を求めてください．また，そのときyがxに比例するかどうか答えてください．
(1)１個が10(g)のイチゴx個の合計の重さをy(g)とする．
（解答）
y=10x，yはxに比例する
(2)１個が10(g)のイチゴx個を50(g)のケースに入れて全体の重さをy(g)とする．
（解答）
y=10x+50，yはxに比例しない
(3)右図のように縦の長さが3(m)，横の長さがx(m)の長方形の面積をy(m2)とする．
（解答）
y=3x，yはxに比例する
(4)右図のように一辺の長さがx(m)の正方形の面積をy(m2)とする．
（解答）
y=x2，yはxに比例しない
(5)１日当たり宿題を3頁済ませる生徒がx日間で済ませられる分量をy頁とする．
（解答）
y=3x，yはxに比例する
(6)全部で30頁ある宿題を，１日当たり宿題を3頁済ませる生徒がx日間がんばったとき，残りの宿題の分量をy頁とする．
（解答）
y=30−3x=−3x+30，yはxに比例しない
(7)次の表で示されるxとyの関係
x12345678910
y2468101214161820
（解答）
y=2x，yはxに比例する
(8)次の表で示されるxとyの関係
x12345678910
y10987654321
（解答）
x+y=11 → y=−x+11，yはxに比例しない

※以下の問題では，正しい選択肢をクリックしてください．

【問題１】
(1)次の関係について
i)yをxで表す式を求めてください．
ii)また，そのときyがxに比例するかどうか答えてください．
１個3(kg)の重りをx個もつとき，重りの合計をy(kg)とする．
i)
y=x+3 y=3−x y=3x y=x3
ii)
比例する 比例ではない
(2)次の関係について
i)yをxで表す式を求めてください．
ii)また，そのときyがxに比例するかどうか答えてください．
１辺の長さがx(m)の正方形の周の長さをy(m)とする．
i)
y=x+4 y=2x y=4x y=x2
ii)
比例する 比例ではない
(3)次の関係について
i)yをxで表す式を求めてください．
ii)また，そのときyがxに比例するかどうか答えてください．
1(g)当たり2(cm)伸びる右図のようなバネで，重さx(g)の重りをつるしたとき，バネが伸びた長さをy(cm)とする．
（ただし，バネが正常に測れる範囲内の重さを使うものとする）

i)
y=x+4 y=2x y=4x y=x2
ii)
比例する 比例ではない
(4)次の関係について
i)yをxで表す式を求めてください．
ii)また，そのときyがxに比例するかどうか答えてください．
自然長（重りを付けないときの長さ）が5(cm)のバネで，1(g)当たり2(cm)伸びるものがある．重さx(g)の重りをつるしたとき，バネの全長をy(cm)とする．
（ただし，バネが正常に測れる範囲内の重さを使うものとする）

i)
y=x+5 y=2x y=2x+5 y=10x
ii)
比例する 比例ではない
.
(5)次の関係について
i)yをxで表す式を求めてください．
ii)また，そのときyがxに比例するかどうか答えてください．
右図のような水槽でＡの栓を開くと毎分5(cm)水位が高くなる．またＢの栓を開くと毎分10(cm)水位が低くなる．初め水位が50(cm)あったとき，Ｂの栓を開いてx分経過したときの水位をy(cm)とする．

i)
y=10x y=−10x
y=10x−50 y=50−10x
ii)
比例する 比例ではない
(6)次の表で示されるxとyの関係について
x12345678910
y45678910111213
i)yをxで表す式を求めてください．
ii)また，そのときyがxに比例するかどうか答えてください．
i)
y=3x y=4x y=x+3 y=x+4
ii)
比例する 比例ではない
...メニューに戻る
■このサイト内のGoogle検索■

△このページの先頭に戻る△
【 アンケート送信 】
… このアンケートは教材改善の参考にさせていただきます

■この頁について，良い所，悪い所，間違いの指摘，その他の感想があれば送信してください．
○文章の形をしている感想は全部読ませてもらっています．
○感想の内で，どの問題がどうであったかを正確な文章で伝えていただいた改善要望に対しては，可能な限り対応するようにしています．（※なお，攻撃的な文章になっている場合は，それを公開すると筆者だけでなく読者も読むことになりますので，採用しません．）


質問に対する回答の中学版はこの頁，高校版はこの頁にあります