類題１−１
ａ１＝３，　ａｎ＋１＝−２ａｎ＋６　（ｎ≧１）　　のとき，一般項ａｎを求める問題
ａｎ＋１＝ｐａｎ＋ｑ　は　ａｎ＋１ーα＝ｐ（ａｎーα）に変形できます．
ａｎ＋１−［ア］＝−２（ａｎ−［ア］）　と変形でき，数列｛ａｎ−［ア］｝は公比−２の等比数列となる．
 

［ア］＝

（→解答を見る）

類題１−２
ａ１＝１，　ａｎ＋１＝３ａｎ＋４　（ｎ≧１）　　のとき，一般項ａｎを求める問題
ａｎ＋１＋［イ］＝３（ａｎ＋［イ］）　と変形でき，数列｛ａｎ＋［イ］｝は公比３の等比数列となる．
 

［イ］＝

（→解答を見る）
類題１−３
ａ１＝２，　ａｎ＋１＝(ａｎ＋１)　（ｎ≧１）　　のとき，一般項ａｎを求める問題
ａｎ＋１−［ウ］＝（ａｎ−［ウ］）　と変形でき，数列｛ａｎ＋［ウ］｝は公比の等比数列となる．
 

［ウ］＝

←メニューに戻る　←問題へ戻る
（→解答を見る）
類題２−１
ａ１＝１，　ａｎ＋１＝ａｎ＋３　（ｎ≧１）　　のとき，一般項ａｎを求める問題
ａｎ＋１＝ａｎ＋ｆ（ｎ）　は，ｆ（ｎ）の和をSｎで表わすと，ａｎ＋１＝ａｎ＋Sn-Sn-1　→　ａｎ＋１−Sn＝ａｎ-Sn-1　と変形できます．
なお，この説明方法は通常の説明方法と異なるので混乱しないようしてください．通常は階差数列からａnを求めますが，ここでは階差数列を使わずに答案を作成しています．
ａｎ＋１−[エ]ｎ＝ａｎ−［エ］(ｎ−１)　と変形でき，数列｛ａｎ−［エ］(ｎ−１)｝は公比１の等比数列（各項が同じ数列）となる．(n=1でもよい．)
 
 

［エ］＝

（→解答を見る）

類題２−２
ａ１＝１，　ａｎ＋１＝ａｎ＋２ｎ−１　（ｎ≧１）　　のとき，一般項ａｎを求める問題
ａｎ＋１＝ａｎ＋ｆ（ｎ）　は，ｆ（ｎ）の和をSｎで表わすと，ａｎ＋１＝ａｎ＋Sn-Sn-1　→　ａｎ＋１−Sn＝ａｎ-Sn-1　と変形できます．
なお，この説明方法は通常の説明方法と異なるので混乱しないようしてください．通常は階差数列からａnを求めますが，ここでは階差数列を使わずに答案を作成しています．
ａｎ＋１−{　[オ]ｎ(ｎ＋１)−［カ］ｎ　｝＝ａｎ−｛　［オ］（ｎ−１）ｎ−［カ］（ｎ−１）　｝　と変形でき，
数列｛ａｎ−｛　［オ］（ｎ−１）ｎ−［カ］（ｎ−１）　｝は公比１の等比数列（各項が同じ数列）となる．
 
 

［オ］＝，　［カ］＝

←メニューに戻る　←問題へ戻る
（→解答を見る）

類題２−３
ａ１＝１，　ａｎ＋１＝ａｎ＋２ｎ　（ｎ≧１）　　のとき，一般項ａｎを求める問題
Σ２ｋ＝２（２ｎ−１）　です．
ａｎ＋１−［キ］（２ｎ−１）＝ａｎ−［キ］（２ｎ-1−１）　と変形でき，数列｛ａｎ−［キ］（２ｎ-1−１）｝は公比１の等比数列（各項が同じ数列）となる．
 
 

［キ］＝

（→解答を見る）

類題３−１
ａ１＝０，　ａｎ＋１＝２ａｎ＋ｎ２　（ｎ≧１）　　のとき，一般項ａｎを求める問題　　（H12同志社大学経済学部入試問題の一部引用）
（実際の試験問題は，解法指定の誘導問題となっています）
ａｎ＋１＋αｎ２＋βｎ＋γ＝２{ａｎ＋α(ｎ-1)２＋β(ｎ-1)＋γ}　となるα，β，γを求めると，

α＝，　β＝，　γ＝

このとき，数列｛ａｎ＋α(ｎ-1)２＋β(ｎ-1)＋γ｝は公比２の等比数列となる．

←メニューに戻る　←問題へ戻る
（→元の問題の解答を見る）

類題３−２
ａ１＝１，　ａｎ＋１＝２ａｎ＋ｎ　（ｎ＝１，２，３，・・・）　　のとき，一般項ａｎを求める問題　　（H12大阪教育大学入試問題の一部引用）
ａｎ＋１＋αｎ＋β＝２{ａｎ＋α(ｎ-1)＋β}　となるα，βを求めると，

α＝，　β＝

このとき，数列｛ａｎ＋α(ｎ-1)＋β｝は公比２の等比数列となる．

（→元の問題の解答を見る）

類題３−３
ａ１＝２，　ａｎ＋１＝３ａｎ＋２ｎ２−２ｎ−１　（ｎ＝１，２，３，・・・）　　のとき，一般項ａｎを求める問題　　（H12岐阜大学入試問題の一部引用）
（実際の試験問題は，解法指定の誘導問題となっています）
ａｎ＋１＋αｎ２＋βｎ＋γ＝３{ａｎ＋α(ｎ-1)２＋β(ｎ-1)＋γ}　となるα，β，γを求めると，

α＝，　β＝，　γ＝

このとき，数列｛ａｎ＋α(ｎ-1)２＋β(ｎ-1)＋γ｝は公比３の等比数列となる．

←メニューに戻る　←問題へ戻る
（→元の問題の解答を見る）

類題４−１
ａ１＝２，　ａｎ＋１＝２ａｎ＋３ｎ　（ｎ＝１，２，３，・・・）　　のとき，一般項ａｎを求める問題　
ａｎ＋１−α・３ｎ+1＝２（ａｎ−α・３ｎ）　となるαを求めると，

α＝

このとき，数列｛ａｎ−α・３ｎ｝は公比２の等比数列となる．

（→解答を見る）
類題４−２
ａ１＝１，　ａｎ＋１＝３ａｎ＋２・５ｎ-1＋４ｎ　（ｎ＝１，２，３，・・・）　　のとき，一般項ａｎを求める問題　
ａｎ＋１−α・５ｎ−β（ｎ+1）−γ＝３（ａｎ−α・５ｎ-1−βｎ−γ）　となるα，β，γを求めると，

α＝，　β＝，　γ＝

このとき，数列｛ａｎ−α・５ｎ-1−βｎ−γ｝は公比３の等比数列となる．

←メニューに戻る　←問題へ戻る
（→解答を見る）
類題４−３
ａ１＝２，　ａｎ＋１＝３ａｎ＋３ｎ　（ｎ＝１，２，３，・・・）　　のとき，一般項ａｎを求める問題　
ａｎ＋１−α・(n+1)３ｎ＝３（ａｎ−α・ｎ３ｎ-1）　となるαを求めると，

α＝

このとき，数列｛ａｎ−α・ｎ３ｎ-1｝は公比３の等比数列となる．

（→解答を見る）
・・・＞　類題５は，問題と答のみとしました．
類題５−１
　
（解答）
類題５−２
　ａ１＝１，　nａn+1＝(n+1)ａｎ
類題５−３
　ａ１＝１，　nａn+1＝(n+2)ａｎ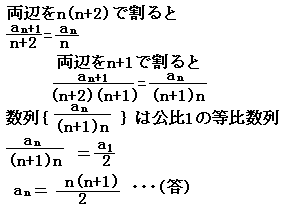

類題８−１
ａ１＝０，　ａ２＝１，ａｎ＋２−６ａｎ＋１＋８ａｎ＝０　（ｎ＝１，２，３，・・・）　　のとき，一般項ａｎを求める問題　　
ａｎ＋２−αａｎ＋１＝β（ａｎ＋１−αａｎ）となるα，βを求めると

α＝，　β＝
または
α＝，　β＝

このとき，数列｛ａｎ＋１−αａｎ｝は公比βの等比数列となる．

←メニューに戻る　←問題へ戻る
（→元の問題の解答を見る）
類題８−２
ａ１＝０，　ａ２＝１，ａｎ＋２−４ａｎ＋１＋４ａｎ＝０　（ｎ＝１，２，３，・・・）　　のとき，一般項ａｎを求める問題　　
ａｎ＋２−αａｎ＋１＝β（ａｎ＋１−αａｎ）となるα，βを求めると

α＝，　β＝（重解）

このとき，数列｛ａｎ＋１−αａｎ｝は公比βの等比数列となる．

※　重解になるときは連立方程式ができませんので，さらに２項間漸化式を解きます．虚数解になるような問題があれば面白いことになるでしょう．
（→元の問題の解答を見る）
類題８−３
ａ１＝１，　ａ２＝２，ａｎ＋２＋ａｎ＋１−６ａｎ＝−４　（ｎ＝１，２，３，・・・）　　のとき，一般項ａｎを求める問題　　
ａｎ＋２−αａｎ＋１−ｐ＝β（ａｎ＋１−αａｎ−ｐ）となるα，β，ｐを求めると

α＝，　β＝，　ｐ＝
または
α＝，　β＝，　ｐ＝

このとき，数列｛ａｎ＋１−αａｎ−ｐ｝は公比βの等比数列となる．

←メニューに戻る　←問題へ戻る
（→元の問題の解答を見る）

類題９−１
ａ１＝１，　ｂ１＝１，　ａｎ＋１＝ａｎ＋３ｂｎ，　ｂｎ＋１＝３ａｎ＋ｂｎ（ｎ＝１，２，３，・・・）　　のとき，一般項ａｎ，ｂｎを求める問題
ａｎ＋１−αｂｎ＋１＝β(ａｎ−αｂｎ)　となるα，βを求めると
ａｎ＋３ｂｎ−α(３ａｎ＋ｂｎ)＝β(ａｎ−αｂｎ)の係数を比較して
α＝，β＝
または　α＝ - 1，β＝
（→元の問題の解答を見る）

類題９−２
ａ１＝０，　ｂ１＝−２，　ａｎ＋１＝−ａｎ−ｂｎ，　ｂｎ＋１＝ａｎ−３ｂｎ（ｎ＝１，２，３，・・・）　　のとき，一般項ａｎ，ｂｎを求める問題
ａｎ＋１−αｂｎ＋１＝β(ａｎ−αｂｎ)　となるα，βを求めると
−ａｎ−ｂｎ−α(ａｎ−３ｂｎ)＝β(ａｎ−αｂｎ)の係数を比較して
α＝，β＝

※　重解のときは，連立方程式にならないので，このあとｂｎを消去してａｎの二項間漸化式を解きます．虚数解になるような問題があれば面白いことになるでしょう．
（→元の問題の解答を見る）

類題９−３
ａ１＝２，　ｂ１＝３，　ａｎ＋１＝ａｎ−８ｂｎ＋１６，　ｂｎ＋１＝ａｎ＋７ｂｎ−１３（ｎ＝１，２，３，・・・）　　のとき，一般項ａｎ，ｂｎを求める問題
(ａｎ＋１−α)＝(ａｎ−α)−８(ｂｎ−β)
(ｂｎ＋１−β)＝(ａｎ−α)＋７(ｂｎ−β)　となるα，βを求めると
α−α＋８β＝１６，　β−α−７β＝−１３　よりα＝１，β＝２
(ａｎ＋１−１)＝(ａｎ−１)−８(ｂｎ−２)
(ｂｎ＋１−２)＝(ａｎ−１)＋７(ｂｎ−２)
ここでａｎ−１＝Aｎ，ｂｎ−２＝Bｎとおくと
Aｎ＋１＝Aｎ−８Bｎ
Bｎ＋１＝Aｎ＋７Bｎ
Aｎ＋１＋ｐBｎ＋１＝ｑ（Aｎ＋ｐBｎ）となるｐ，ｑを求めると（ｐ，ｑ）＝（２，３），（４，５）
Aｎ＋１＋２Bｎ＋１＝３（Aｎ＋２Bｎ）より，数列｛Aｎ＋２Bｎ｝は公比□の等比数列
Aｎ＋２Bｎ＝(A１＋２B１)□n-1
Aｎ＋１＋４Bｎ＋１＝５（Aｎ＋４Bｎ）より，数列｛Aｎ＋４Bｎ｝は公比○の等比数列
Aｎ＋４Bｎ＝(A１＋４B１)○n-1

□＝，○＝

←メニューに戻る　←問題へ戻る
（→元の問題の解答を見る）

 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 

←メニューに戻る　←問題へ戻る


解答
＜類題１−１＞　ａｎ＝（−２）n-1＋２　　＜類題１−２＞　ａｎ＝３n−２　＜類題１−３＞　ａｎ＝（）n-1＋１
＜類題２−１＞　ａｎ＝３ｎ−２　　　　　　＜類題２−２＞　ａｎ＝ｎ２−２ｎ＋２　　＜類題２−３＞　ａｎ＝２n−１
＜類題３−１＞　ａｎ＝3・2n−ｎ2−2ｎ−3　　＜類題３−２＞　ａｎ＝３・２n-1−ｎ−１　　＜類題３−３＞　ａｎ＝３n−ｎ２
＜類題４−１＞　ａｎ＝３n−２ｎ−１　＜類題４−２＞　ａｎ＝３n＋５ｎ−１−２ｎ−１　＜類題４−３＞　ａｎ＝（ｎ＋１）３n−１
＜類題８−１＞　ａｎ＝（４n−１−２ｎ−１）／２　＜類題８−２＞　ａｎ＝（ｎ−１）２n-2　＜類題８−３＞　ａｎ＝（２n−１−（−３）ｎ−１＋５）／５
＜類題９−１＞　ａｎ＝ｂｎ＝４n−１　＜類題９−２＞　ａｎ＝(１−ｎ)(−２)n−１，ｂｎ＝(−ｎ−１）（−２）n−１　＜類題９−３＞　ａｎ＝２・３n−５ｎ＋１，ｂｎ＝(５n−３ｎ＋４)／２

 ↑類題に戻る