|
○ 2次関数y=ax2+bx+c=0 (ただしa≠0)のグラフとx軸との共有点(交点または接点)のx座標は、2次方程式ax2+bx+c=0の解で与えられます。 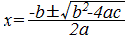 2次関数y=ax2+bx+c=0のグラフとx軸との共有点の個数は、2次方程式ax2+bx+c=0の解の個数と一致します。 ○ D=b2−4acを使えば、解の公式は次の形に書けるので、解の個数はDの符号で決まります。 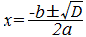
(1) D>0 → 解は2個 → 2次関数のグラフとx軸の共有点は2個
【例】 x2+2x−3=0 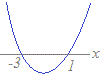 → D=16>0
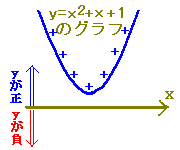
→ D=16>0→ 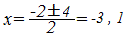 :実数解は2個 :実数解は2個→ y=x2+2x−3とx軸の共有点は2個 (2) D=0 → 解は1個 → 2次関数のグラフとx軸の共有点は1個 【例】 x2+2x+1=0 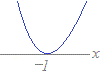 → D=0
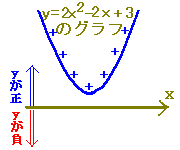
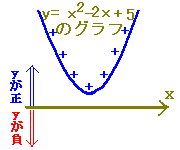
→ D=0→ 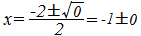 :実数解は1個 :実数解は1個→ y=x2+2x+1とx軸の共有点は1個 (3) D<0 → 解はない → 2次関数のグラフとx軸の共有点はない 【例】 x2+2x+3=0 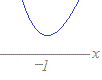 → D=−8<0
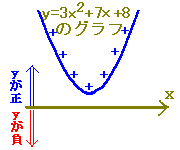
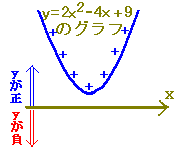
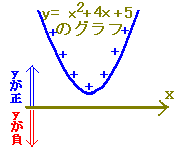
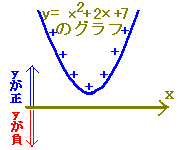
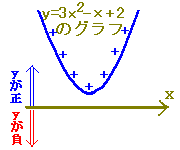
→ D=−8<0→ 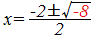 :実数解はない :実数解はない→ y=x2+2x+3とx軸の共有点はない ※ 2次不等式を解くときに実際に答案に書くのは、上記のうちで の部分で、 の部分は「グラフに関係ない」ものなので書きません。 ■2次不等式の解き方一覧■ 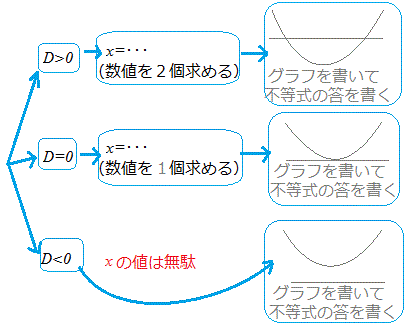 |
○ 解の公式に登場する根号の中身b2−4acを判別式といいDで表します。(Dはdiscriminant(判別式)の略) D=b2−4ac
#よくある間違い No.1#
D= 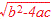 ×(判別式は根号ではない) ×(判別式は根号ではない)D=b2−4ac ○(判別式は根号の中身) [例] 2次方程式x2+2x+3=0について D= D=22−4·1·3=−8 ○(根号の中身) ○ D≧0のとき、2次方程式の解 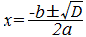 は2個または1個の実数を表しますが、D<0のときは実数にはなりません。 は2個または1個の実数を表しますが、D<0のときは実数にはなりません。このような根号の中が負の値になる数は虚数と呼ばれ高校数学IIで習います。 Dが虚数なのではない# D<0 ⇔ xが虚数
#よくある間違い No.2#
D=+ ← こんな書き方はない。正しくはD>0 D=− ← こんな書き方はない。正しくはD<0 D=0=0 ← 0が0に等しいと言っても無駄 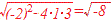 <0 ← そもそも虚数には大小はない。 <0 ← そもそも虚数には大小はない。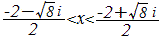 ← 複素数や虚数を習ったからといってこんな答案を書いてはいけない。そもそも虚数には大小はない。 ← 複素数や虚数を習ったからといってこんな答案を書いてはいけない。そもそも虚数には大小はない。(あなたが「何も分かっていない」ことが採点官にばれてしまう)
■D<0のときの2次不等式の解き方(まとめ)■
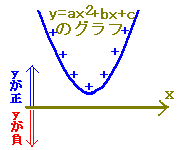 <問題の形> <答の形> ax2+bx+c>0(a>0) → xはすべての数 ax2+bx+c≧0(a>0) → xはすべての数 ax2+bx+c<0(a>0) → 解なし ax2+bx+c≦0(a>0) → 解なし  だから
だから問題が 式>0なら ⇒xはすべての数 問題が 式<0なら ⇒解なし 問題が式≧0なら 「>0」でもよいし「=」でもよいということ.ところで「=」となるxの値はないが,すべてのxについて「>0」になっているのだから,全部よいということ ⇒xはすべての数 問題が 式≦0なら 「<0」でもよいし「=」でもよいということ.ところで「=」となるxの値はなく,「<0」となるxもないのだから ⇒解なし |