|
■多項式、分数関数、無理関数の不定積分
【内容】
この頁では次のような関数の不定積分を扱う。 (1) 5x3dx , x(2x+1)dx , (3x−4)5dxなど ……多項式の不定積分(数学II の復習) (2) dx , dxなど ……分数関数の不定積分 (3) dx , dx , x− dxなど ……無理関数の不定積分
【公式】
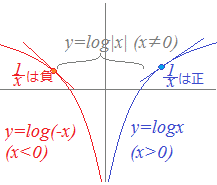
(I) xαdx=+C(α≠−1) α=−1のときだけは例外として、次の公式による。 (II) dx=log|x|+C ≪証明≫ 各々微分してみると分かる。 (1) ← xα=αxα−1だから()=xα (2) ← log x= (x>0) またlog(−x)= − = (x<0) だから、log|x|= (x≠0) |
数学III で登場する多項式、分数関数、無理関数の不定積分は左の公式だけでは処理できず、部分分数分解、置換積分、部分積分などの公式も合わせて使う。したがって、この頁を読むには部分分数分解、置換積分、部分積分などの項目を先に読んでおく必要がある。 多項式はxn(nは0以上の整数)の形の式の定数倍・和・差なので、左の(I)の公式でαに0以上の整数をあてはめると求められる。 分数関数は=x− n(nは正の整数)、=(2x+1)− 1 などと負の指数で表せるので、左の(I)の公式でαに負の整数を当てはめると求められる。 無理関数は=x、=(2x+3) などと分数の指数で表せるので、左の(I)の公式でαに分数を当てはめると求められる。 一般にαが−1以外の実数であればα=のような無理数の場合も含めて、左の公式(1)が成り立つ(証明は対数微分法による)が、高校ではαが無理数の問題はめったに扱わない。 ※次の表において、αが分数であることと分数関数とは対応しておらず、αが無理数であることと無理関数とは対応していないことに注意。
 |
||||||
|
例1 ■多項式の不定積分■ (1) 5x3dx= x4+C(←x3dx= x4+C) (2) x(2x+1)dx=(2x2+x)dx= x3+x2+C (←積の形になっている式は、展開して和差の形にしてから積分する) (3) (3x+2)3dx
3x+2=tとおいて置換積分を行う
=3 → dx= (3x+2)3dx=t3= +C= +C |
(4) x(x+1)3dx
展開したくない方(次数の高い方のかっこ内)を1文字にする:x+1=tとおいて置換積分を行う
=1 → dx=dt…(i) x=t−1…(ii) (i)(ii)を代入 x(x+1)3dx=(t−1)t3dt=(t4−t3)dt= − +C = − +C=(x+1)4( − )+C = +C |
||||||
|
◇問題1◇ 次の不定積分を求めよ。(正しいものを選べ。) ※ 計算用紙が必要です。 (1) (x+2)(x−3)dx 2x−1+C − −6x+C (x+2)( − 3x)+C ( +2x)( −3x)+C (2) (2x−3)4dx +C +C +C 4(2x−3)3+C |
(3) (x−1)(x+2)2dx +C +C +C +C |
||||||
|
例2 ■分数関数の不定積分■ 分数関数の積分では x−1dx= dx=log|x|+C の形だけが例外で、他の次数については dx=x−ndx= +C(α≠−1) による。 なお、「割り算によって分子の次数を下げておくこと」や「部分分数分解」などの前処理が必要となることが多い。 (1)
2x+1=tとおいて置換積分を行う
=2 → dx= = · = log|t|+C= log|2x+1|+C 一般に
= log|ax+b|+C(a≠0)
が成り立つ。(置換積分ができれば、これ自体を覚える必要はない。)
(2) dx
割り算をして商と余りに分け、商を整数部分に余りを分子とする。これにより
(x+3)÷(x+1)=1 ··· 2 → =1+ dx=(1+ )dx=x+2log|x+1|+C (3) dx=3x−2dx=3 +C=−3x−1+C = − +C (4) dx
展開したくないもの(分母)のかっこ内を1文字にする:x−1=tとおいて置換積分を行う
=1 → dx=dt…(i) 2x+1=2(t+1)+1=2t+3…(ii) dx= ( )dt= ( + )dt =( + 3t−2 )dt=2log|t|− +C=2log|x−1|− +C |
■分母が2次式(以上)になっているもの■
(5)
(a) 分母が(ax+b)2の形になっている(D=0型)とき ⇒ax+b=tとおいて置換積分するとよい(左の(4)) (b) 分母が1次式の積に因数分解できるとき(D>0型)とき ⇒部分分数分解により分母を1次式に直す(下の(5)) (c) 分母が(実数の範囲では)因数分解できないとき(D<0型)とき ⇒(*)特急券( f’(x)/f(x) 型)が使えないかどうか確かめる(下の(6))
(**)それがだめなら、 分母=x2+a2 (a>0) → x=a tan tの置換積分(下の(7))
部分分数分解により分母を1次式にする。
x2−4=(x−2)(x+2)だから = = ( − ) ※この係数は = + とおいて、恒等式の係数比較によりa,bを求めた結果を使う。 = ( − )dx = (log|x−2|−log|x+2|)+C= log||+C (6) dx
[次の形のもの→即答可能:特急券あり]
(証明)dx=log|f(x)|+C f(x)=tとおいて置換積分を行うと =f’(x) → f’(x)tx=dt dx= dt =log|t|+C=log|f(x)|+C (x2+2x+5)’=2x+2だから dx= log|x2+2x+5|+C = log(x2+2x+5)+C (∵x2+2x+5>0) (7) ※この形の「不定積分」を表すためには逆三角関数tan−1xを要するので、現行教育課程の問題としてはほとんど出題されない。ただし、「定積分」は単なる数値になるので定積分の問題としては出題できる。 x=2tan t → = dx= dt x2+4=4tan2t+4=4(tan2t+1) = dt ここで、三角比の相互関係の公式:tan2t+1= により、(tan2t+1)(cos2t)=1 = = t+C= tan−1 +C
tan t=xのとき、t=tan−1xと書く。
この記号(逆三角関数)を使えば、 a tan t=x → tan t= → t=tan−1 |
||||||
|
◇問題2◇ 次の不定積分を求めよ。(正しいものを選べ。) ※ 計算用紙が必要です。 (1) +C 3log|3x−2|+C log|3x−2|+C +C (2) dx x+7log|x−3|+C x+2log|x−3|+C +C − x +C (3) dx +C − +C − + +C + +C (4) log|(x−1)(x+1)| +C log|| +C log|(x−1)(x+1)| +C log|| +C |
(5) dx log|2x| +C log(x2+1) +C log|2x(x2+1)| +C log|| +C (6) log(x2+2) +C log|| +C tan−1 +C tan−1 +C |
||||||
|
例3 ■無理関数の不定積分■ (1) dx=xdx= x +1+C= x+C = x · x+C= x +C (2) dx
3x+2=tとおいて置換積分を行う
=3 → dx= dx==t = t+C = t+C= (3x+2)+C (3) (3x+4)− dx
3x+4=tとおいて置換積分を行う
=3 → dx= (3x+4)− dx=t− = t+C= +C = +C |
(4) dx
=tとおいて置換積分を行う
x+2=t3 → x=t3−2 = 3t2 → dx=3t2dt dx= 3t2dt=(3t4−6t)dt = t5−3t2+C = −3 +C = { (x+2)−3}+C= +C |
||||||
|
◇問題3◇ 次の不定積分を求めよ。(正しいものを選べ。) ※ 計算用紙が必要です。 (1) 2+C +C +C +C (2) dx +C +C (2x+3) · +C (2x+3) · +C |
(3) xdx x2+ +C +C (x+1)2 +C (x+1)(3x−2)+C |