|
|
|
|
 �T�D�����_�̍��W
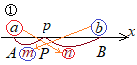
�T�D�����_�̍��W�@��������̂Q�_A(a), B(b)�����Ԑ���AB��m:n�ɓ�������_��P(p)�Ƃ���ƁC���Wp�̒l�� �ɓ������D
## �댯�ȗ��Ƃ��� ##
•���q�� a�Ɋ|���Ă���̂́C�u�}�ʼn������̔䗦n�v b�Ɋ|���Ă���̂́C�u�}�ʼn������̔䗦m�v �ł��邱�Ƃɒ��� �� �u�����������v�u�ւ��Ȃ������v���Ɗo���Ă����Ƃ悢 |
�i�ؖ��j �}�@�ɂ�����
�A�j a<b�̂Ƃ�
AP=p−a, PB=b−p������
AP:PB=m:n��� (p−a):(b−p)=m:n (�����̐�)=(�O���̐�)�ɂ���āC���̎���ʏ�̓����ɒ����� n(p−a)=m(b−p) np−na=mb−mp (m+n)p=na+mb
�C�j a>b�̂Ƃ��C�r���o�߂Ŏ��̕������ς�邪�C�Ō�̎��͓����ɂȂ�
(a−p):(p−b)=m:n ��� |
|
�@���̊e��ɑ��āC�������I�������N���b�N�i�^�b�v�j���Ă��������D�i�����̓��Ă�I������C�r���o�߂Ɖ��o�܂��j
�y���1�z
����������@�@��������̂Q�_A(2), B(9)�����Ԑ���AB��3:4�ɓ�������_��P(p)�Ƃ���Ƃ��C���Wp�̒l�����߂Ă��������D 3 4 5 6 7 |
�y���2�z
����������@�@��������̂Q�_A(6), B(−2)�����Ԑ���AB��5:3�ɓ�������_��P(p)�Ƃ���Ƃ��C���Wp�̒l�����߂Ă��������D 0 1 2 3 4 |
|
�y���3�z
����������@�@��������̂Q�_A(−3), B(5)�����Ԑ���AB��3:2�ɓ�������_��P(p)�Ƃ���Ƃ��C���Wp�̒l�����߂Ă��������D |
�y���4�z
����������@�@��������̂Q�_A(−3), B(−7)�����Ԑ���AB��2:1�ɓ�������_��P(p)�Ƃ���Ƃ��C���Wp�̒l�����߂Ă��������D |
 �U�D�O���_�̍��W
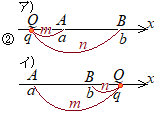
�U�D�O���_�̍��W�@��������̂Q�_A(a), B(b)�����Ԑ���AB��m:n�ɊO������_��Q(q)�Ƃ���ƁC���Wq�̒l�� �ɓ������D
## �댯�ȗ��Ƃ��� ##
•�������������������āCm, n�̂����P�����̐��ɂ���ƁC�O�������ɂȂ邪�C�Q�Ƃ����̐��ɏ��������Ă��܂��ƁC���̓��������ɖ߂��Ă��܂��̂ŁC�v���� |
�i�ؖ��j �}�A�ɂ�����
�A�j a<b, m<n�̂Ƃ�
AQ=a−q, QB=b−q������
AQ:QB=m:n��� (a−q):(b−q)=m:n (�����̐�)=(�O���̐�)�ɂ���āC���̎���ʏ�̓����ɒ����� n(a−q)=m(b−q) na−nq=mb−mq (m−n)q=−na+mb ����ƕ��q�ɂ��ꂼ��−1���|���Ă��C�����̒l�͕ς��Ȃ�����C�O�������͎��̌`�ŏ����Ă��悢�D �i�����v�Z�������̐��k�����ɁC�um��n�̏����������}�C�i�X�ɂ���v�Ƃ����������̐搶�������D��������ƕ��ꂪ���ɂȂ��āC�����̊ԈႢ������炵���D�j
�C�j a<b, m>n�̂Ƃ��C�r���o�߂Ŏ��̕������ς�邪�C�Ō�̎��͓����ɂȂ�
(q−a):(q−b)=m:n ��� �E�ja>b, m<n�̂Ƃ��C�G�ja>b, m>n�̂Ƃ������l�ɂ��āC�r���o�߂͕ς�邪�ŏI���ʂ͈�v����D |
|
�@���̊e��ɑ��āC�������I�������N���b�N�i�^�b�v�j���Ă��������D�i�����̓��Ă�I������C�r���o�߂Ɖ��o�܂��j
�y���5�z
����������@�@��������̂Q�_A(3), B(7)�����Ԑ���AB��1:5�ɊO������_��Q(q)�Ƃ���Ƃ��C���Wq�̒l�����߂Ă��������D −8 −2 2 |
�y���6�z
����������@�@��������̂Q�_A(4), B(1)�����Ԑ���AB��5:2�ɊO������_��Q(q)�Ƃ���Ƃ��C���Wq�̒l�����߂Ă��������D −6 −1 0 1 6 |
|
�y���7�z
����������@�@��������̂Q�_A(−2), B(3)�����Ԑ���AB��1:5�ɊO������_��Q(q)�Ƃ���Ƃ��C���Wq�̒l�����߂Ă��������D |
�y���8�z
����������@�@��������̂Q�_A(−1), B(−5)�����Ԑ���AB��5:3�ɊO������_��Q(q)�Ƃ���Ƃ��C���Wq�̒l�����߂Ă��������D −11 −5 1 5 11 |