| (1) |
|
[数II][図形と方程式][2点間の距離.三角形の形状]
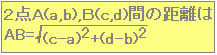 三角形の形状を調べる問題では、「まず三辺の長さを計算」、次に下のどれに該当するか検討します。 1 AB=BCなど → 二等辺三角形 2 AB=BC=CAなど → 正三角形 3 AB2+BC2=CA2など →∠B=90°の直角三角形 4 AB2+BC2=CA2,AB=BCなど →∠B=90°の直角二等辺三角形 左の問題では AB2=22+32=13 BC2=32+22=13 CA2=52+12=26 だからAB=BCかつ∠Bは直角 |
| (2) |
[数II][図形と方程式][分点の座標.重心の座標]
 左の問題では点Aの座標を(x,y)とおくと x=6,y=15 |
|
| (3) |
[数II][図形と方程式][2点を通る直線の方程式.一直線上にある条件]
 左の問題ではABを通る直線の方程式を求めてからCの座標を代入します。 AB: y-3=2(x-4) → y=2x-5 Cを代入: p=6p-5 p=1 |
|
| (4) |
[数II][図形と方程式][2直線の垂直条件]
○  ○2つの直線y=mx+kとy=m'x+k'が垂直 → mm’=-1 左の問題では直線ABの方程式y=-3x+7 点(3,-2)を通り傾き1/3の直線の方程式 →y+2=1/3(x-3) → x-3y-9=0 |
|
| (5) |
[数II][図形と方程式][対称移動]
左の問題では,求める点Bの座標を(p,q)とおくとき 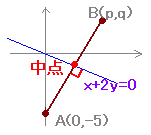 ABの中点が与えられた直線上にあること・・(1) ABが与えられた直線に垂直になること・・(2) からp,qを求められます。 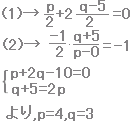 |
|
| (6) |
[数II][図形と方程式][円の方程式]
○円の移動は中心の移動だけで考える。半径は変わらない。 ○点対称移動 点P(p,q)に関して点A(a,b)と対称な点Qの座標を(x,y)とするとAはPQの中点 左の問題では, 中心の座標は(3,-4)→中点(2,1)→(1,6)となります。 |
|
| (7) |
[数II][図形と方程式][3点を通る円の方程式]
○求める方程式をx2+y2+ax+by+c=0とおき 点の座標を代入してa,b,cを連立方程式から求める 左の問題では, 求める方程式をx2+y2+ax+by+c=0とおくと (0,0)を通る→c=0 (4,0)を通る→16+4a+c=0 (1,3)を通る→1+9+a+3b+c=0 より a=-4,b=-2,c=0 |
|
| (8)
y=2x,y=-3x |
[数II][図形と方程式][円の接線]
○円と直線が接する条件は, ア) yを消去してxの2次方程式について(判別式)=0とする方法 イ) 中心と直線との距離が半径に等しいとする方法 があります。 左の問題をア)の方法で解くと 原点を通る直線の方程式をy=mxとおき (x-1)2+(mx-3)2=5 x2-2x+1+m2x2-6mx+9=5 (m2+1)x2-2(3m+1)x+5=0 D’=(3m+1)2-5(m2+1)=0 2m2+3m-2=0 (2m-1)(m+2)=0 m=1/2,-2 |
|
| (9) |
[数II][図形と方程式][軌跡の方程式]
○媒介変数を消去してxとyの関係式にするのが基本です。 左の問題では 円の方程式を変形すると (x-a)2+(y-2a+1)2=1となり 中心の座標は x=a,y=2a-1となります。 これより媒介変数aを消去して y=2x-1 |
|
| (10) |
[数II][図形と方程式][不等式と領域]
○円(x-a)2+(y-b)2=r2の内側 → (x-a)2+(y-b)2 < r2 ○円(x-a)2+(y-b)2=r2の外側 → (x-a)2+(y-b)2 > r2 |