|
[7] チェビシェフの不等式
○次の不等式をチェビシェフの不等式といいます.この不等式では登場する文字が必ずしも正の数とは限らないことに注意しましょう」.
a≦b, x≦yのとき
 \( \dfrac{a+ b}{2}\cdot\dfrac{x+ y}{2}\leqq \dfrac{ax+ by}{2} \)…(1) \( \dfrac{a+ b}{2}\cdot\dfrac{x+ y}{2}\leqq \dfrac{ax+ by}{2} \)…(1)
等号は a=bまたはx=yのとき
a≦b≦c, x≦y≦zのとき
 \( \dfrac{a+ b+ c}{3}\cdot\dfrac{x+ y+ z}{3}\leqq\dfrac{ax+ by+ cz}{3} \)…(2) \( \dfrac{a+ b+ c}{3}\cdot\dfrac{x+ y+ z}{3}\leqq\dfrac{ax+ by+ cz}{3} \)…(2)
等号は a=b=cまたはx=y=zのとき
※文字数がn個×2のときも同様の関係が成り立つ
この不等式を証明するためには,仮定の使い方を考えることが重要です.
b−a≧0, y−x≧0の形を作るしかない!
(証明)
(1)←
仮定より
b−a≧0, y−x≧0
(右辺)−(左辺) \( =\dfrac{ax+ by}{2}-\dfrac{a+ b}{2}\cdot\dfrac{x+ y}{2} \) \( =\dfrac{ax+ by}{2}-\dfrac{a+ b}{2}\cdot\dfrac{x+ y}{2} \)
-(a%2B b)(x%2B y)}{4}) \( =\dfrac{2(ax+ by)-(a+ b)(x+ y)}{4} \) \( =\dfrac{2(ax+ by)-(a+ b)(x+ y)}{4} \)
 \( =\dfrac{2ax+2by-ax-ay-bx-by}{4} \) \( =\dfrac{2ax+2by-ax-ay-bx-by}{4} \)
 \( =\dfrac{ax+ by-ay-bx}{4} \) \( =\dfrac{ax+ by-ay-bx}{4} \)
%2B b(y-x)}{4}) \( =\dfrac{a(x-y)+ b(y-x)}{4} \) \( =\dfrac{a(x-y)+ b(y-x)}{4} \)
(y-x)}{4}\underline{\ge}0) \( =\dfrac{(b-a)(y-x)}{4}\geqq0 \) \( =\dfrac{(b-a)(y-x)}{4}\geqq0 \)
等号はa=bまたはx=yのとき
(21)←
仮定より
b−a≧0, c−b≧0, y−x≧0, z−y≧0
(右辺)−(左辺) \( =\dfrac{ax+ by+ cz}{3}-\dfrac{a+ b+ c}{3}\cdot\dfrac{x+ y+ z}{3} \) \( =\dfrac{ax+ by+ cz}{3}-\dfrac{a+ b+ c}{3}\cdot\dfrac{x+ y+ z}{3} \)
-(a%2B b%2B c)(x%2B y%2B z)}{9}) \( =\dfrac{3(ax+ by+ cz)-(a+ b+ c)(x+ y+ z)}{9} \) \( =\dfrac{3(ax+ by+ cz)-(a+ b+ c)(x+ y+ z)}{9} \)
 \( =\dfrac{1}{9}(3ax+ 3by+ 3cz-ax-ay-az \) \( =\dfrac{1}{9}(3ax+ 3by+ 3cz-ax-ay-az \)
) \( -bx-by-bz-cx-cy-cz) \) \( -bx-by-bz-cx-cy-cz) \)
 \( =\dfrac{1}{9}(2ax+ 2by+ 2cz-ay-az \) \( =\dfrac{1}{9}(2ax+ 2by+ 2cz-ay-az \)
) \( -bx-bz-cx-cy) \) \( -bx-bz-cx-cy) \)
) \( =\dfrac{1}{9}\{(2ax-ay-az) \) \( =\dfrac{1}{9}\{(2ax-ay-az) \)
) \( +(2by-bx-bz) \) \( +(2by-bx-bz) \)
\}) \( +(2cz-cx-cy)\} \) \( +(2cz-cx-cy)\} \)
\hspace{70}%2B a(x-z)) \( =\dfrac{1}{9}\{a(x-y)\hspace{70px}+a(x-z) \) \( =\dfrac{1}{9}\{a(x-y)\hspace{70px}+a(x-z) \)
%2B b(y-z)) \( + b(y-x)+ b(y-z) \) \( + b(y-x)+ b(y-z) \)
%2B c(z-x)\}) \( +c(z-y)+ c(z-x)\} \) \( +c(z-y)+ c(z-x)\} \)
(y-x)%2B(c-b)(z-y)%2B(c-a)(z-x)\}) \( =\dfrac{1}{9}\small{\{(b-a)(y-x)+(c-b)(z-y)+(c-a)(z-x)\} }\) \( =\dfrac{1}{9}\small{\{(b-a)(y-x)+(c-b)(z-y)+(c-a)(z-x)\} }\)
ここでb−a≧0, c−b≧0, c−a≧0, y−x≧0, z−y≧0, z−x≧0だから(右辺)≧(左辺)が成り立つ.
等号はa=b=cまたはx=y=zのとき
【例題7.1】
a, b>0のとき
 \( \dfrac{a^2+b^2}{2}\cdot\dfrac{a^3+ b^3}{2}\leqq\dfrac{a^5+ b^5}{2} \) \( \dfrac{a^2+b^2}{2}\cdot\dfrac{a^3+ b^3}{2}\leqq\dfrac{a^5+ b^5}{2} \)
が成り立つことを証明してください.
一見,チェビシェフの不等式がそのまま使えそうに見えますが,その前提条件a≦bが満たされておらず,代わりにa, b>0となっていることに注意
仕方がないので,初めから自分で証明する方がよい
(解答)
(右辺)−(左辺) \( =\dfrac{a^5+b^5}{2}-\dfrac{a^2+ b^2}{2}\cdot\dfrac{a^3+b^3}{2} \) \( =\dfrac{a^5+b^5}{2}-\dfrac{a^2+ b^2}{2}\cdot\dfrac{a^3+b^3}{2} \)
 \( =\dfrac{2a^5+2b^5-a^5-a^2b^3-a^3b^2-b^5}{4} \) \( =\dfrac{2a^5+2b^5-a^5-a^2b^3-a^3b^2-b^5}{4} \)
 \( =\dfrac{a^5+b^5-a^2b^3-a^3b^2}{4} \) \( =\dfrac{a^5+b^5-a^2b^3-a^3b^2}{4} \)
%2B b^3(b^2-a^2)}{4}) \( =\dfrac{a^3(a^2-b^2)+b^3(b^2-a^2)}{4} \) \( =\dfrac{a^3(a^2-b^2)+b^3(b^2-a^2)}{4} \)
(a^2-b^2)}{4}) \( =\dfrac{(a^3-b^3)(a^2-b^2)}{4} \) \( =\dfrac{(a^3-b^3)(a^2-b^2)}{4} \)
a>b(>0)のとき \( a^2\gt b^2,\hspace{3px}a^3\gt b^3 \)だから \( a^2\gt b^2,\hspace{3px}a^3\gt b^3 \)だから
(右辺)>(左辺)
(0<)a≦bのとき \( a^2\leqq b^2,\hspace{3px}a^3\leqq b^3 \)だから \( a^2\leqq b^2,\hspace{3px}a^3\leqq b^3 \)だから
(右辺)≧(左辺)
いずれの場合も,(右辺)≧(左辺)が成り立つ.(等号はa=bのとき)
→右上に続く
|
【例題7.2】
0<a≦b≦cのとき
(a^3%2B b^3%2B c^3)\underline{\le}3(a^5%2B b^5 %2B c^5)&chf=bg,s,ffffdd) \( (a^2+ b^2+ c^2)(a^3+ b^3+ c^3)\leqq3(a^5+ b^5 + c^5) \) \( (a^2+ b^2+ c^2)(a^3+ b^3+ c^3)\leqq3(a^5+ b^5 + c^5) \)
が成り立つことを証明してください.
大学入試の記述式答案では「高校の教科書に書いてある定理・公式は黙って使ってもよい」「高校の教科書に書いてない定理・公式は黙って使ってはいけない」というのが通常の採点基準でしょう.
チェビシェフの不等式は,ほとんどの教科書に書いてないので,使うときは「証明してから使う」「公式名と公式を書いてから使う」方が無難でしょう.
(解答)
仮定より0<a≦b≦cだから0<a2≦b2≦c2および0<a3≦b3≦c3が成り立つ.
チェビシェフの不等式
p≦q≦r, x≦y≦zのとき
 \( \dfrac{p+ q+ r}{3}\cdot\dfrac{x+ y+ z}{3}\leqq\dfrac{px+ qy+ rz}{3} \) \( \dfrac{p+ q+ r}{3}\cdot\dfrac{x+ y+ z}{3}\leqq\dfrac{px+ qy+ rz}{3} \)
等号は p=q=rまたは x=y=zのとき
において,p=a2, q=b2, r=c2およびx=a3, y=b3, z=c3とおくと
 \( \dfrac{a^2+ b^2+ c^2}{3}\cdot\dfrac{a^3+ b^3+ c^3}{3}\leqq\dfrac{a^5+ b^5+ c^5}{3} \) \( \dfrac{a^2+ b^2+ c^2}{3}\cdot\dfrac{a^3+ b^3+ c^3}{3}\leqq\dfrac{a^5+ b^5+ c^5}{3} \)
したがって
(a^3%2B b^3%2B c^3)\underline{\le}3(a^5%2B b^5%2B c^5)) \( (a^2+ b^2+ c^2)(a^3+ b^3+ c^3)\leqq 3(a^5+ b^5+ c^5) \) \( (a^2+ b^2+ c^2)(a^3+ b^3+ c^3)\leqq 3(a^5+ b^5+ c^5) \)
が成り立つ.
等号は0<a2=b2=c2または0<a3=b3=c3から
a=b=cのとき
【問題7】 正しいものを選んでください.(選択肢のうち正しいものをクリック)
(1)
(0<)a≦b≦cのとき
(a^2%2B b^2%2B c^2)(a^3%2B b^3%2B c^3)&chf=bg,s,ffffdd) \( (a+ b+ c)(a^2+ b^2+ c^2)(a^3+ b^3+ c^3) \) \( (a+ b+ c)(a^2+ b^2+ c^2)(a^3+ b^3+ c^3) \)
&chf=bg,s,ffffdd) \( \leqq k(a^6+ b^6+ c^6) \) \( \leqq k(a^6+ b^6+ c^6) \)
を満たす定数 kの最小値は
1
2
3
4
6
9
仮定より 0<a≦b≦cだから 0<a2≦b2≦c2および 0<a3≦b3≦c3が成り立つ.
チェビシェフの不等式
p≦q≦r, x≦y≦zのとき
 \( \dfrac{p+ q+ r}{3}\cdot\dfrac{x+ y+ z}{3}\leqq\dfrac{px+ qy+ rz}{3} \) \( \dfrac{p+ q+ r}{3}\cdot\dfrac{x+ y+ z}{3}\leqq\dfrac{px+ qy+ rz}{3} \)
等号は p=q=rまたは x=y=zのとき
において, p=a, q=b, r=cおよび x=a2, y=b2, z=c2とおくと
 \( \dfrac{a+ b+ c}{3}\cdot\dfrac{a^2+ b^2+ c^2}{3}\leqq\dfrac{a^3+ b^3+ c^3}{3} \) \( \dfrac{a+ b+ c}{3}\cdot\dfrac{a^2+ b^2+ c^2}{3}\leqq\dfrac{a^3+ b^3+ c^3}{3} \)
さらに, p=a3, q=b3, r=c3および x=a3, y=b3, z=c3とおくと
 \( \dfrac{a^3+ b^3+ c^3}{3}\cdot\dfrac{a^3+ b^3+ c^3}{3}\leqq\dfrac{a^6+ b^6+ c^6}{3} \) \( \dfrac{a^3+ b^3+ c^3}{3}\cdot\dfrac{a^3+ b^3+ c^3}{3}\leqq\dfrac{a^6+ b^6+ c^6}{3} \)
したがって
 \( \dfrac{a+ b+ c}{3}\cdot\dfrac{a^2+ b^2+ c^2}{3}\cdot\dfrac{a^3+ b^3+ c^3}{3} \) \( \dfrac{a+ b+ c}{3}\cdot\dfrac{a^2+ b^2+ c^2}{3}\cdot\dfrac{a^3+ b^3+ c^3}{3} \)
 \( \leqq\dfrac{a^3+ b^3+ c^3}{3}\cdot\dfrac{a^3+ b^3+ c^3}{3} \) \( \leqq\dfrac{a^3+ b^3+ c^3}{3}\cdot\dfrac{a^3+ b^3+ c^3}{3} \)
 \( \leqq\dfrac{a^6+ b^6+ c^6}{3} \) \( \leqq\dfrac{a^6+ b^6+ c^6}{3} \)
ゆえに
(a^2%2B b^2%2B c^2)(a^3%2B b^3%2B c^3)\underline{\le}9(a^6%2B b^6%2B c^6)&chs=370x26) \( (a+ b+ c)(a^2+ b^2+ c^2)(a^3+ b^3+ c^3)\small{\leqq 9}(a^6+ b^6+ c^6) \) \( (a+ b+ c)(a^2+ b^2+ c^2)(a^3+ b^3+ c^3)\small{\leqq 9}(a^6+ b^6+ c^6) \)
すなわち, kの最小値は9
(2)
a≦b≦c, x≦2y≦3z, a+b+c=0のとき
 \( ax+ 2by+ 3cz \) \( ax+ 2by+ 3cz \)の最小値は
−3
−2
−1
0
1
2
3
チェビシェフの不等式
p≦q≦r, s≦t≦uのとき
 \( \dfrac{p+ q+ r}{3}\cdot\dfrac{s+ t+ u}{3}\leqq\dfrac{ps+ qt+ ru}{3} \) \( \dfrac{p+ q+ r}{3}\cdot\dfrac{s+ t+ u}{3}\leqq\dfrac{ps+ qt+ ru}{3} \)
等号は p=q=rまたは s=t=uのとき
において, p=a, q=b, r=cおよび s=x, t=2y, u=3zとおくと
 \( \dfrac{a+ b+ c}{3}\cdot\dfrac{x+ 2y+ 3z}{3}\leqq\dfrac{ax+ 2by+ 3cz}{3} \) \( \dfrac{a+ b+ c}{3}\cdot\dfrac{x+ 2y+ 3z}{3}\leqq\dfrac{ax+ 2by+ 3cz}{3} \)
仮定により a+b+c=0だから
 \( 0\leqq ax+ 2by+ 3cz \)
x=2y=3z \( 0\leqq ax+ 2by+ 3cz \)
x=2y=3z(たとえば x=6, y=3, z=2)のとき,最小値0となる
(3)
(0<)a≦b≦cのとき,次の不等式の Aの箇所に入る式を求めてください
^n\underline{\le}\hspace{3}A\hspace{3}(a^n%2B b^n%2B c^n)&chf=bg,s,ffffdd) \( (a+ b+ c)^n\leqq\hspace{3px}A\hspace{3px}(a^n+ b^n+ c^n) \) \( (a+ b+ c)^n\leqq\hspace{3px}A\hspace{3px}(a^n+ b^n+ c^n) \)
2
3
2n−1
3n−1
2n
3n
チェビシェフの不等式
p≦q≦r, s≦t≦uのとき
 \( \dfrac{p+ q+ r}{3}\cdot\dfrac{s+ t+ u}{3}\leqq\dfrac{ps+ qt+ ru}{3} \) \( \dfrac{p+ q+ r}{3}\cdot\dfrac{s+ t+ u}{3}\leqq\dfrac{ps+ qt+ ru}{3} \)
等号は p=q=rまたは s=t=uのとき
において, p=a, q=b, r=cおよび s=a, t=b, u=cとおくと
 \( \dfrac{a+ b+ c}{3}\cdot\dfrac{a+ b+ c}{3}\leqq\dfrac{a^2+ b^2+ c^2}{3} \) \( \dfrac{a+ b+ c}{3}\cdot\dfrac{a+ b+ c}{3}\leqq\dfrac{a^2+ b^2+ c^2}{3} \)
だから
^2\underline{\le}\frac{a^2%2B b^2%2B c^2}{3}) \( \Bigl(\dfrac{a+ b+ c}{3}\Bigr)^2\leqq\dfrac{a^2+ b^2+ c^2}{3} \) \( \Bigl(\dfrac{a+ b+ c}{3}\Bigr)^2\leqq\dfrac{a^2+ b^2+ c^2}{3} \)
さらに
^2\Bigl(\frac{a%2B b%2B c}{3}\Bigr)\underline{\le}\Bigl(\frac{a^2%2B b^2%2B c^2}{3}\Bigr)\Bigl(\frac{a%2B b%2B c}{3}\Bigr)) \( \Bigl(\dfrac{a+ b+ c}{3}\Bigr)^2\small{\Bigl(\dfrac{a+ b+ c}{3}\Bigr)\leqq}\Bigl(\dfrac{a^2+ b^2+ c^2}{3}\Bigr)\small{\Bigl(\dfrac{a+ b+ c}{3}\Bigr)} \) \( \Bigl(\dfrac{a+ b+ c}{3}\Bigr)^2\small{\Bigl(\dfrac{a+ b+ c}{3}\Bigr)\leqq}\Bigl(\dfrac{a^2+ b^2+ c^2}{3}\Bigr)\small{\Bigl(\dfrac{a+ b+ c}{3}\Bigr)} \)
) \( \leqq\Bigl(\dfrac{a^3+ b^3+ c^3}{3}\Bigr) \) \( \leqq\Bigl(\dfrac{a^3+ b^3+ c^3}{3}\Bigr) \)
だから
^3\underline{\le}\Bigl(\frac{a^3%2B b^3%2B c^3}{3}\Bigr)) \( \Bigl(\dfrac{a+ b+ c}{3}\Bigr)^3\leqq\Bigl(\dfrac{a^3+ b^3+ c^3}{3}\Bigr) \) \( \Bigl(\dfrac{a+ b+ c}{3}\Bigr)^3\leqq\Bigl(\dfrac{a^3+ b^3+ c^3}{3}\Bigr) \)
以下同様にして
^n\underline{\le}\Bigl(\frac{a^n%2B b^n%2B c^n}{3}\Bigr)) \( \Bigl(\dfrac{a+ b+ c}{3}\Bigr)^n\leqq\Bigl(\dfrac{a^n+ b^n+ c^n}{3}\Bigr) \) \( \Bigl(\dfrac{a+ b+ c}{3}\Bigr)^n\leqq\Bigl(\dfrac{a^n+ b^n+ c^n}{3}\Bigr) \)
ゆえに
^n\underline{\le}3^{n-1}(a^n%2B b^n%2B c^n)) \( (a+ b+ c)^n\leqq3^{n-1}(a^n+ b^n+ c^n) \) \( (a+ b+ c)^n\leqq3^{n-1}(a^n+ b^n+ c^n) \)
|
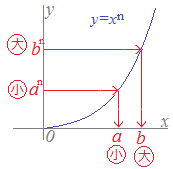
 イ) ベクトルの内積で考える方法
イ) ベクトルの内積で考える方法