|
【三角関数の合成公式】
(解説)a sinθ+b cosθの形の式は一つの三角関数にまとめることができます.これを三角関数の合成公式といいます.
a sinθ+b cosθ=sin(θ+α)
(ただし,αはcosα=, sinα=となる角)○ 三角関数の加法定理sinαcosβ+cosαsinβ=sin(α+β)により,sinθcosα+cosθsinα=sin(θ+α)となります. ○ たまたまa, bが,ある一つの角度αの三角関数cosα, sinαに等しいとき,たとえば
a==cos60°, b==sin60°
のようになっているとき
sinθ+ cosθ=sinθ cos60°+cosθ sin60°
と書けることになります.=sin(θ+60°) 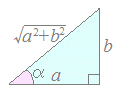 ○ しかし,一般にはa·sinθ+b·cosθのように与えられた係数,a, bがそのままで一つの角度αの三角関数cosα, sinαに等しいことはめったにありません.
○ しかし,一般にはa·sinθ+b·cosθのように与えられた係数,a, bがそのままで一つの角度αの三角関数cosα, sinαに等しいことはめったにありません.右図のようにa, bが2辺となっている直角三角形を考えると, cosα=, sinα= が成り立ちますので,この形が使えるように与えられた式をうまく割り算して調整します.
a sinθ+b cosθ
=sinθ+cosθ = (sinθ +cosθ ) 図のような直角三角形の角度をαとすると, =cosα, =sinαとなるから
(sinθ +cosθ )
と書けることになります.= (sinθcosα+cosθsinα ) = sin(θ+α) 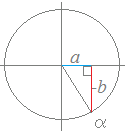 ○ a sinθ−b cosθ (a,b>0)を ○ a sinθ−b cosθ (a,b>0)を(sinθ·cosα+cosθ·sinα) =sin(θ+α) cosα= sinα= の式を使って合成するときは,右図のような第4象限の角αを考えていることになります. 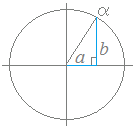 ○ a sinθ−b cosθ (a,b>0)を ○ a sinθ−b cosθ (a,b>0)を(sinθ·cosα−cosθ·sinα) =sin(θ−α) cosα= sinα= の式を使って合成するときは,右図のような第1象限の角αを考えていることになります. |
※ 紛らわしい公式との区別
○関数が同じ,角度が違う⇒公式あり
○関数が違う,角度が同じ⇒公式あり ×関数も角度も違う⇒公式なし 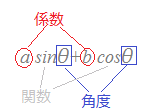 (1) 係数と関数が同じなら,角度が違ってもよい
(1) 係数と関数が同じなら,角度が違ってもよい
sinA±sinB,cosA±cosB
⇒和積の公式 (2) 角度が同じなら,係数と関数が違ってもよい
asinθ+bcosθ
⇒合成公式 (*) 関数も角度も違えば公式がない
sinA+cosB
(*) 係数と角度が違えば公式がない⇒対応する公式はない
asinA±bsinB,acosA±bcosB
⇒対応する公式はない
【例題1】
次の三角関数を合成してください. sinθ+cosθ 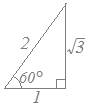 (解答) (解答)右図のように斜辺の長さが==2となる直角三角形を考えると cos60°=, sin60°= となるから sinθ+cosθ =2(sinθ+cosθ) =2(sinθ·cos60°+cosθ·sin60°) =2sin(θ+60°)
理論上は,余弦の加法定理
cosθcosα−sinθsinα=cos(θ+α) cosθcosα+sinθsinα=cos(θ−α) を使って,次のように変形することもできますが,一つできれば十分なので,余弦を使った合成の方はあまり見かけません. sinθ+cosθ =cosθ+sinθ =2(cosθ+sinθ) =2(cosθcos30°+sinθsin30°) =2cos(θ−30°) 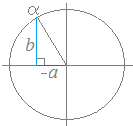 ○ −a sinθ+b cosθ (a,b>0)を ○ −a sinθ+b cosθ (a,b>0)を(sinθ·cosα+cosθ·sinα) =sin(θ+α) cosα= sinα= の式を使って合成するときは,右図のような第2象限の角αを考えていることになります.  ○ −a sinθ+b cosθ (a,b>0)を ○ −a sinθ+b cosθ (a,b>0)を−(sinθ·cosα−cosθ·sinα) =−sin(θ−α) 振幅を正の値にする必要があるときは sin(α−θ) cosα= sinα= の式を使って合成するときは,右図のような第1象限の角αを考えていることになります. |
|
【例題2】
次の三角関数を合成してください. 3sinθ+4cosθ 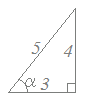 (解答) (解答)右図のように斜辺の長さが==5となる直角三角形を考えると cosα=, sinα= となるから 3sinθ+4cosθ =5(sinθ +cosθ ) =5(sinθ·cosα+cosθ·sinα) =5sin(θ+α) (ただし,αはcosα=, sinα=となる角)
※このように,角度αを具体的な数値としてでなく,cosα, sinαの値で表す方法も可能です.
|
【例題3】
次の三角関数を合成してください. 2sinθ−cosθ 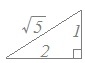 (解答) (解答)右図のように斜辺の長さが=となる直角三角形を考えると cosα=, sinα= となるから 2sinθ−cosθ =(sinθ −cosθ ) =(sinθ·cosα−cosθ·sinα) =sin(θ−α) (ただし,αはcosα=, sinα=となる角)
この問題では,sin(θ−β)の式を使って合成しましたが,sin(θ+β)の式を使って合成するときは,
cosβ=, sinβ=−となる角β(第4象限の角) を用いて,sin(θ+β)と表してもよい. |
|
【問題1】
(空欄に入るものを下から選んでください)次の三角関数を合成してください. sinθ+cosθ =だから sinθ+cosθ=(sinθ·+cosθ·) cosα=? 解答 1 1
とおくと,sinθ+cosθ=(sinθ·cos45°+cosθ·sin45°)となるから
30°
45°
60°
90°sin(θ+45°) |
【問題2】
(空欄に入るものを下から選んでください)次の三角関数を合成してください. 3sinθ+2cosθ 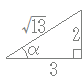 =だから,右図のような直角三角形を考えると
=だから,右図のような直角三角形を考えるとcosα=?解答 2 3 2 3 sin(θ+α) sin(θ−α) cos(θ+α) cos(θ−α) |
|
【問題3】
(空欄に入るものを下から選んでください)次の三角関数を合成してください. 3sinθ−4cosθ  =5だから,右図のような直角三角形を考えると
=5だから,右図のような直角三角形を考えるとcosα=?解答 |
5sin(θ+α) 5sin(θ−α) 5cos(θ+α) 5cos(θ−α) |
|
【例題4】
0°≦θ<360°のときy=sinθ+cosθの最大値,最小値及びそのときのθの値を求めてください.  (解答) (解答)右図のように斜辺の長さが=2となる直角三角形を考えると cos60°=, sin60°= となるから sinθ+cosθ =2(sinθ +cosθ ) =2(sinθ·cos60°+cosθ·sin60°) =2sin(θ+60°) 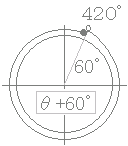 0°≦θ<360°のとき60°≦θ+60°<420°だから
0°≦θ<360°のとき60°≦θ+60°<420°だから
−1≦sin(θ+60°)≦1
θ+60°=90°→θ=30°のとき最大値2−2≦2sin(θ+60°)≦2 θ+60°=270°→θ=210°のとき最小値−2 |
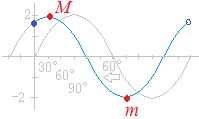 ※教科書や参考書では,右図のように三角関数のグラフを描いて問題を解く方法が示されていることもあります.
※教科書や参考書では,右図のように三角関数のグラフを描いて問題を解く方法が示されていることもあります.実際に生徒の手の動きを観察していると,グラフを描く方法では
○ヘッドホン=耳あての図がお薦め
 |
|
【問題4】
(空欄に入るものを下から選んでください)0°≦θ<360°のときy=sinθ−cosθの最大値,最小値及びそのときのθの値を求めてください. 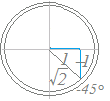 =だから,右のような図を考えると
=だから,右のような図を考えるとsinθ−cosθ=sin(θ−45°) ここで0°≦θ<360°のときθ−45°の値の範囲は?解答 0°≦θ−45°<360° −45°≦θ−45°<315° 45°≦θ−45°<405° 0°≦θ−45°<315° 1 −1 − −1 − − |
【問題5】
(空欄に入るものを下から選んでください)0°≦θ<360°のときy=sinθ+cosθの最大値,最小値及びそのときのθの値を求めてください. 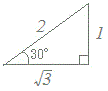 =2だから,
=2だから,y=2(sinθ·+cosθ·) =2(sinθ·cos30°+cosθ·sin30°) =2sin(θ+30°) ここで0°≦θ<360°のときθ+30°の値の範囲は?解答 0°≦θ+30°<360° −30°≦θ+30°<330° 0°≦θ+30°<390° 30°≦θ+30°<390° 1 −1 2 −2 −1 1 2 −2 |
|
【問題6】
(空欄に入るものを下から選んでください)0°≦θ<360°のときy=4sinθ−3cosθの最大値,最小値を求めてください.  =5だから,右図のような直角三角形を考えるとy=5sin(θ−α)
=5だから,右図のような直角三角形を考えるとy=5sin(θ−α)ただし,αはcosα=, sinα=となる第1象限の角 ここで0°≦θ<360°のとき 0°−α≦θ−α<360°−α θ−α=90°すなわちθ=90°+αのとき,最大値 ? 解答
5
1
1+α
5
5+α
→閉じる← |
−5
−1
−1+α
−5
−5+α
→閉じる← |
|
■[個別の頁からの質問に対する回答][三角関数の合成公式について/17.3.7]
はじめの方の解説や問題はすごく良かったのですが、問題の解説がなくて、分からなかった時に困ってしまいました…。自力で、サイトの最初の方から読み直して解決したのですが、問題の解説はやはりあった方が良いと思われます。
■[個別の頁からの質問に対する回答][三角関数の合成公式について/17.2.20]
=>[作者]:連絡ありがとう.「最初の方から読み直して解決」するように意図したものです.読み直したときにあいまいな知識がはっきりしてくるので,それが身に付く読み方です.・・・一般に直線的に読み進むのでなく,行ったり来たりしながら読む方が身に付くと言えます. わかりやすかったです!
最後にテスト形式でチェックできるのは助かります
■[個別の頁からの質問に対する回答][三角関数の合成公式について/17.2.19]
=>[作者]:連絡ありがとう. 角度はラジアン(π)を使って表して欲しい
=>[作者]:連絡ありがとう.角度の単位をラジアンにしなければならないのは,三角関数の微積分を行うときです.それ以外では両方とも使います. |