|
■問題→公式チェック1■ ･･･レベル：章末問題，公務員試験，採用試験 ....................○身に付いていない項目をチェックして補強する問題です。初めて学習するのには、適していません。 ....................○使用法： 解答後まとめて[採点]してください。[ヒント]ボタンを押した問題は引き分けとなります。10問で30分を目標にしてください。 (1) (教科書の問のレベル) θが第2象限の角でsinθ=  のとき，cosθの値は
|
 |
[数II][三角関数][三角関数の相互関係]
○第2象限ではcosθの符号は負 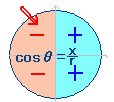 ○ cos2θ=1-sin2θ=1-4/9=5/9 の平方根の負の方を答えます。 |
| (2)(教科書の問のレベル) | |
[数II][三角関数][sinθ，cosθの対称式]
○ sin2θ+cos2θ=1を利用すると 和の値←→積の値(一方が分かれば他方も分かる) ○ sinθ+cosθ=  より(sinθ+cosθ)2=( )2sin2θ+2sinθcosθ+cos2θ=1/25 1+2sinθcosθ=1/25 2sinθcosθ=-24/25 sinθcosθ=-12/25 |
| (3)(教科書の問のレベル) | |
[数II][三角関数][三角関数の性質]
○ 次の図で±sinθ，±cosθに読み替えます。 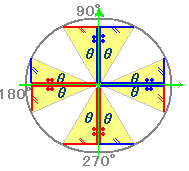 ○ sin(270°+θ)=・・/r = -cosθ sin(90°+θ)=・・/r = cosθ sin(180°-θ)=〃/r = sinθ cos(180°+θ)=・・/r = -cosθ cos(270°-θ)=〃/r = -sinθ |
| (4)(教科書の問のレベル) | |
[数II][三角関数][三角関数の周期]
○ y=sinθ,cosθの周期は2π y=sin mθ, cos mθの周期は2π/m y=tanθの周期はπ y=tan mθの周期はπ/m 振幅,平行移動は周期に影響しない。 ○問題の関数の周期は2π/2=π 各選択肢の周期は各々 2π/4，2π/3，π/2，π |
| (5)(教科書の問のレベル) | |
[数II][三角関数][三角方程式] ○ 定義域を変換する： 0≦x＜2π→0≦2x＜4π 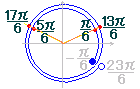→-  ≦φ=2x-＜ ○ sinφ=  (-≦φ＜)を解く 図により，φ= ， ， ， 2x- =，，，2x=  ，π， ，3πx= ， ， ， |
| (6)(教科書の問のレベル) | |
[数II][三角関数][三角不等式] ○ 定義域を変換する 0≦x＜2π→0≦  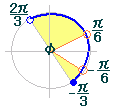＜π→- ≦φ=-＜  ○- ≦φ＜-，＜φ＜→0≦ｘ＜ ，π＜ｘ＜2π |
| (7)(教科書の問のレベル) | |
[数II][三角関数][三角不等式]
○ cos2x=1-sin2xを用いてsinxだけで表わす。 ○ 2(1-sin2x)+7sinx-5＞0 2sin2x-7sinx+3＜0 (2sinx-1)(sinx-3)＜0 1/2＜sinx＜3 (sinx＜3は常に成立) 1/2＜sinxより  |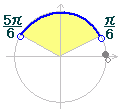
| (8)(教科書の問のレベル) | |
[数II][三角関数][三角関数の合成]
○ 合成するとy= 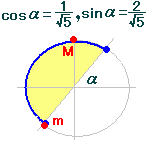 sin(x+α)となる（ここにαは次の式を満たす角度） ○ x+α= のときM=x+α=π+α (x=π) のときm=-2 |
| (9)(教科書の問のレベル) | |
数II][三角関数][三角関数の最大最小] ○ cosx=t とおくと y= 9t2-6t (-1≦t≦1)の最大値，最小値を求めることになります。 ○ y=9{(t-1/3)2-1/9}=9(t-1/3)2-1  |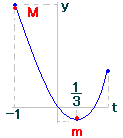
| (10)(教科書の問のレベル) | |
数II][三角関数][一般角]
○ θ=120°→θ/2=60°は第１象限となりますが θ=480°→θ/2=240°は第3象限 θ=-240°→θ/2=-120°は第３象限 ・・・一般的に解決するには一般角で表示 ○ 90°+360°×n＜θ＜180°+360°×ｎ →45°+180°×ｎ＜θ/2＜90°+180°×ｎ 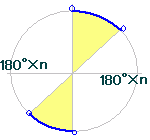 |