|
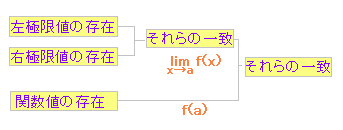
■ 関数の連続,極限関数 ◇解説◇ 関数のグラフが視覚的には「つながっていて,切れ目がない」ときに,連続であるといいます。 これを数式を用いて調べるには,次の定義によります。
◇連続の定義◇
次の関係が成り立つとき,関数 f(x) は x = a において連続であるといいます。(連続でないとき,不連続であるといいます。) f(a) = f(x) ・・・ (1) (*) 詳しくいえば, 関数値 f(a) が存在し,・・・ (2) 極限値 f(x) が存在し,・・・ (3) それらが一致するとき,・・・→(1) 連続であるといいます。 例えば,関数 f(x) = は, x = 0 において, 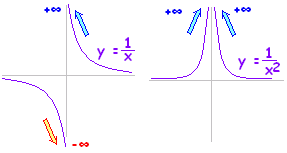
(参考)
教科書や参考書では,[A]「関数が定義されない点については,そもそも連続とか不連続とかの議論ができない」という立場で書かれているものと,[B]他のすべての点で関数が定義されていて,1つの点でのみ関数が定義されていないとき,その点を不連続点として扱う立場で書かれているものとがあります. 理論上は[A]の立場であるべきかもしれませんが,この頁で取り扱っている極限関数について,多くの問題集・参考書の解答との整合性を図るには,[B]の立場で理解する方がわかりやすくなります. [A]の立場から言えば,x = 0で切れているとはいえども,x = 0では関数がないのだから,その点では連続とか不連続といった議論は初めから存在しないこととなります. 高校の初歩的な演習では「グラフが切れている場所を求めよ」とほぼ同じ意味で「不連続点を求めよ」と問うので,上記の2つの例は,この[B]の立場から見て不連続という例に入れています. [B]の立場を採用したからといっても,f(x)=のように広がりのある区間x<0で定義されない関数について,例えばx=−1において連続や不連続の議論はしません. |
(*) さらに詳しくいえば, x が a よりも大きな値をとりながら a に近づくときの極限値(右極限値)と,x が a よりも小さな値をとりながら a に近づくときの極限値(左極限値)とが異なる場合,極限値は存在しないといいます。(どんな近づき方をしても1つの有限確定の値に近づくときに,その値を極限値とします。) 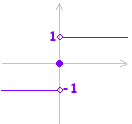
右極限値は f(x) = = 1 左極限値は f(x) = = −1 これらが一致しないので,x → 0 のとき極限値は存在せず,不連続です。
|
|
■例題 (1)
(答案) = = x = 0 = = (−x) = 0 だから f(x) = 0 また,f(0) = 0 f(x) = f(0) が成り立つから x = 0 で連続
※ 極限を用いて定義される関数を「極限関数」といいます。
以下の問題において,必要ならば次の性質を用いて,答えなさい。 (*1) x > 1 のとき xn = ∞ (*2) x = 1 のとき xn = 1 (*3) -1 < x < 1 のとき xn = 0 (*4) x =−1 のとき xn は 存在しない(±1を振動) (*5) x <−1 のとき xn は 存在しない(±∞を振動) |
(2) f(x) = で定義される関数について x = 1 における連続性を調べなさい。 (答案) 1) x > 1 のとき xn = ∞ だから f(x) = = = 1 よって f(x) = 1(定数値をとる関数の極限値はその定数値) 2) −1 < x < 1 のとき xn = 0 だから f(x) = =−1 よって f(x) =−1(定数値をとる関数の極限値はその定数値) 1)2)より,極限値 f(x) が存在しないから,x = 1 のとき不連続 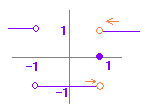 |