|
1
そこで,面積Sを直接求める代わりにSの微分から求めることを考える。(微分が分かれば元の関数は不定積分で求まる。)
|
2
○ 図2のように区間の左端をaに固定しておき、右端の座標をxとすると,囲まれる図形はxの関数
S(x)となる。最終的に求めるものはS(b)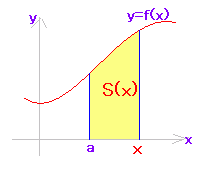
|
|
1
そこで,面積Sを直接求める代わりにSの微分から求めることを考える。(微分が分かれば元の関数は不定積分で求まる。)
|
2
○ 図2のように区間の左端をaに固定しておき、右端の座標をxとすると,囲まれる図形はxの関数
S(x)となる。最終的に求めるものはS(b)
|
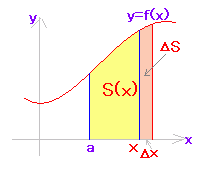
f(x)Δx<ΔS<f(x+Δx)Δx
ゆえに 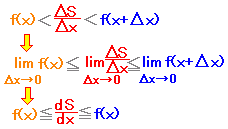 (この結果はf(x)が増加関数でなくても成り立つ) |
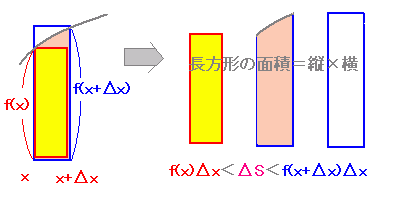 以上より
以上よりf(x)の1つの原始関数をF(x)とおくと S(x)=F(x)+C…(1) ここでS(a)=0だから S(a)=F(a)+C=0 C=−F(a)…(2) (2)を(1)に代入すると S(x)=F(x)−F(a) 求める面積は S=S(b)=F(b)−F(a) |
 【備考】 ※ここでは面積を求めることを導入の話題として定積分の定義を紹介した。実際には,定積分が面積を表わすのは,y=f(x)のグラフがx軸よりも上にある場合で,x軸よりも下の箇所があれば符号が変わる。このような面積の計算は別途取り扱う。  |
※初めて学ぶ人向けの注意※
■ そのまま代入して引くのでなく,(1つの)原始関数(不定積分のCを取ったもの)に代入して引くこと。 ■ F(上) - F(下) の引く順序を間違わないこと。 ■ 不定積分に登場する定数Cは定積分では不要: (F(b) +C) - (F(a) + C) としても,引くと消えるので F(b) -F(a) となり同じこと。Cがない方がよい。 ■ 不定積分については,次の公式を使う。 と書くこともあります.(同じことを表しています) |
|
【例1】
(答案)
(1) まず,1つの原始関数を求めます(C=0の形でよい)
⇒ この問題では (2) 次に,その原始関数に上端の値,下端の値を代入して引きます. ⇒ |
【例2】
(答案)
(1) まず,1つの原始関数を求めます(C=0の形でよい)
⇒ この問題では (2) 次に,その原始関数に上端の値,下端の値を代入して引きます. ⇒ |
|
【例3】
(答案)
(1) まず,1つの原始関数を求めます(C=0の形でよい)
⇒ この問題では (2) 次に,その原始関数に上端の値,下端の値を代入して引きます. ⇒ ※定積分は,面積に対応していることが多いが,x軸との上下関係を考慮せずに単純に計算した場合,負の値になることもある. この頁では,「定積分は計算式」として扱い,負の値になっても気にしないことにする. |
【例4】
(答案)
(1) まず,1つの原始関数を求めます(C=0の形でよい)
⇒ この問題では (2) 次に,その原始関数に上端の値,下端の値を代入して引きます. ⇒ |
|
【問題1】 次の定積分を求めてください.(選択肢の中から正しいものを1つクリック)
クリックして解答すれば採点結果と解説が表示されます.解答しなければ解説は出ません.
(1)
|
(2)
|
|
(3)
|
(4)
|
|
【問題2】 次の定積分を求めてください.(選択肢の中から正しいものを1つクリック)
(1)
|
(2)
|
|
(3)
|
(4)
|
|
(参考)
wxMaximaを使って積分計算の検算を行う方法
(1) wxMaximaを起動すると,画面には何も書かれていない.入力行を作るためにEnterキーを空打ちする.(2) 例えば の問題について i) 不定積分(原始関数)の形を確かめるには
メニュー画面から,微積分→積分と選び,関数の欄に x^2-2*x と書き込む (2x ではなく 2*x と書く←間違いやすい) OKボタンをクリック ⇒ ii) さらに,区間 1≦x≦2 の定積分を求めるには 上記の入力欄 %i1 などにカーソルを合わせて,第3引数の1と第4引数の2を追加する integrate(x^2-2*x, x,1,2); としてから,Shift+Enter ⇒ ※原始関数の形を確かめる必要がなければ,上記の手順を1つにまとめて メニュー画面から,微積分→積分と選び,関数の欄に x^2-2*x と書き込み, 定積分の欄にチェックを入れる→下端 1,上端 2 としてOKボタンをクリック |