|
■データの代表値(平均値,中央値,最頻値)
■平均値
(解説)N個の値x1 , x2 , x3 , ... , xNからなるデータの平均値は 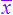 = …(1) = …(1)
x1がf1個
あるのだからx2がf2個 …… xnがfn個 (ただし,f1+f2+f3+...+fn=N) 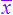 = == = …(2) 多くの数値からなるデータの特徴を1つの数値で表すものは「代表値」と呼ばれます.代表値のうちで最もよく利用され,最も重要なのが平均値です. 平均値は,(値の合計)÷(個数の合計)で定義され,小中学校以来誰もがよく知ってるものです.
【例1】 (Excelを使った計算)
右の表2のように,Excelのワークシート上のA1からA30の範囲にデータがあるとき,(1)式の
分子のx1+x2+x3+ ... +xNは
1つのワークシート関数で平均値を求めるには,
=SUM(A1:A30) で求められます.(結果は,1642) 分母のNは =COUNT(A1:A30) で求められます.(結果は,30) したがって,平均値は =SUM(A1:A30)/COUNT(A1:A30) で求められます.(結果は,54.7)
=AVERAGE(A1:A30)
とします.(結果は,54.7)
(参考)数個の数値の平均では,有効数字は元の数値に合わせますが,この例のように概ね10個以上の数値の平均を求めるときは,有効数字を1桁増やして小数第1位まで求めるとよい・・・何度も測定すれば精度が高くなると考えるとよい.
【例2】 (Excelを使った計算)
右の表3のように,Excelのワークシート上のA1からD11の範囲にデータがあるとき,(2)式の
分子のx1f1+x2f2+x3f3+ ... +xnfnを求めるためには
C列の値とD列の値の積の和(C2*D2+C3*D3+C4*D4+...+C11*D11)を直接求める関数 =SUMPRODUCT() (←積の和)を使えば,分子は
例えば,D列の右隣のE列に =C2*D2 として,まず積x1f1を求めておき 次に,この式をコピーして,E3からE11の範囲に貼り付けます.(式のコピー・貼り付けにより,いわゆる「相対参照」となり,E3には =C3*D3,E4には =C4*D4,E5には =C5*D5,...,E11には =C11*D11が入ります.) さらに,E12に =SUM(E2:E11)とすれば,x1f1+x2f2+x3f3+ ... +xnfnに対応する値になります.(結果は 1660) 分母のN=f1+f2+f3+...+fnは 例えば,D12に =SUM(D2:D11) とすれば求められます.(結果は,30) 以上の準備ができたら,平均値は =E12/D12 で求められます.(結果は,55.3)
(参考)表2のデータを階級幅10の度数分布表にしたものが表3ですが,例えば表2の6や7は表3においてはいずれも階級値5と”みなされる”ので,例1と例2の結果は完全には一致しません.
=SUMPRODUCT(C2:C11,D2:D11)
によって求められます. したがって,平均値は =SUMPRODUCT(C2:C11,D2:D11)/SUM(D2:D11) によって求められます. |
 【よく登場する用語】
【よく登場する用語】「データの大きさ」とは,例えば,右の表で先頭の数値93などの大きさのことではありません. 統計では,何個(何件)の観測値・測定値があるかによって,その資料の信頼性が左右されることが多く,何個(何件)の値があるかに大きな関心があります. 個々の値のことではなく,資料に示された値全体のことを「データ」といい(集合に付けられた名前がデータ),その資料にある値の個数(件数)のことを「データの大きさ」といいます. 【例】 例えば,25人の身長を記録した資料は,「大きさ25のデータ」といいます. 【例】 例えば,500個の豆の重さを記録した資料は,「大きさ500のデータ」といいます. ※ 上の表2,表3はいずれも「大きさ30のデータ」です. (1)式のN,(2)式のf1+f2+f3+...+fn=N, Excelで = COUNT() で計算する値がデータの大きさです. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
【問題1】
Excelを使って,右の表4に示されるデータの平均値を求めてください.(転記するのは大変ですので,画面上でドラッグ&コピーし,Excelのワークシート上に単純に貼り付けて使ってください.) 144.9 245.8 354.7 463.6 HELP
ワークシートの左上端(A1)に貼りつけるものとすると,
=AVERAGE(A1:A15) または =SUM(A1:A15)/COUNT(A1:A15) により45.8となります. →2
【問題2】
Excelを使って,右の表5に示されるデータの平均値を求めてください.(転記するのは大変ですので,画面上でドラッグ&コピーし,Excelのワークシート上に単純に貼り付けて使ってください.) 125.9 226.6 327.2 428.3 HELP
ワークシートの左上端(A1)に貼りつけて,階級値5の値がC2,度数3の値がD6にあるものとすると
=SUMPRODUCT(C2:C6,D2:D6)/SUM(D2:D6) により25.87 となります. →1
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
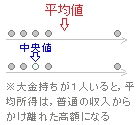 の値を示す訳ではないので,大小2つに分けたときの真ん中の値が必要な場合には,中央値(メジアン)が使われます.
の値を示す訳ではないので,大小2つに分けたときの真ん中の値が必要な場合には,中央値(メジアン)が使われます.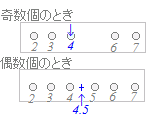
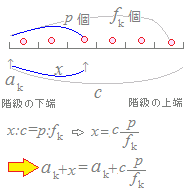
 20から30までの階級を7個の(小)階級に分けて,小さい方から3番目と4番目の中間 20+10/7*3 を求めると,24.2857..≒24.3
20から30までの階級を7個の(小)階級に分けて,小さい方から3番目と4番目の中間 20+10/7*3 を求めると,24.2857..≒24.3