|
■ ■基本 例1
|
例2
|
|
■ ■基本 例1
|
例2
|
| その他の変形
例2’ 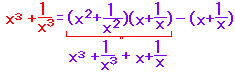 ・・・(2') ・・・(2') |
例3
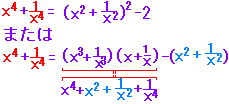 ・・・(3) ・・・(3) |
例4
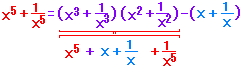 ・・・(4) ・・・(4) |
例5
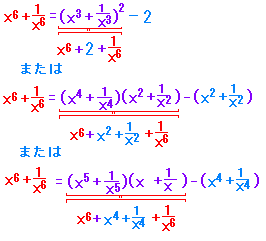 ・・・(5) ・・・(5) |
◆要約◆
適当に積を作り、後で調整します。(「走ってから考える」ということ!-- 変形方法は一つとは限りません。) |
| 例題1
|
答案
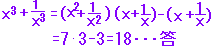 |
例題2
 |
答案
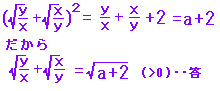 |
|
■==問題==
1
[ヒント][解答]
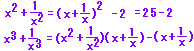
23
110 |
2
[ヒント][解答]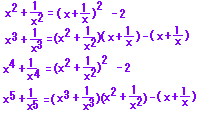
47
123 |
|
[ヒント][解答]
a3-3a
|
4
[ヒント][解答]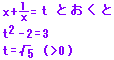 |
|
5
[ヒント][解答]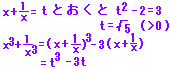
2
5 |
[ヒント][解答]
|
[ヒント][解答]
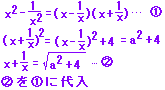 |