■重複順列

　「同じものを繰り返し取ってよいという約束のもとで」できる順列を重複順列といいます。「同じものを繰り返し取ってよいという約束」は、通常「重複を許して」という言葉で表現されます。

　異なるn個のものから重複を許してr個取ってできる順列の総数は、次のように求めることができます。
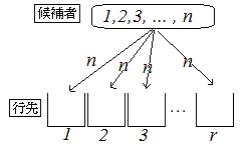
　右図のように、n個の候補者をr個の箱に並べるとき
初めの箱の入れ方はn通り
（ここが重要）一度使ったものを何度でも使えることにすれば、2番目の箱の入れ方はn通り
3番目の以降の箱の入れ方も、すべてn通り

　以上により次の公式が成り立ちます。なお、重複順列の総数はnΠrと書かれることがありますが、この記号を使わなければならないということではありません。（高校の教科書では使われていません）
【重複順列の総数】
　異なるn個のものから重複を許してr個取ってできる順列の総数は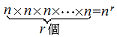

【例1】
　1から9までの数字を使ってできる2桁の正の整数は何通りありますか。ただし、同じ数字を使ってもよいものとします。
（参考）
　1から99までに99個の整数があります。100は3桁の整数です。このうちで、
　01,02,…,09すなわち1,2,…,9の9個は1桁の整数
　10,20,30,…,90 の9個は0を使っているから問題の条件に合いません。
　以上により99個のうち18個が条件に合いませんので81個が条件に合います。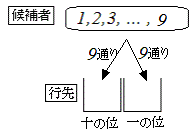
（解答）
　十の位の決め方は1〜9の9通り。
　その各々について一の位の決め方も9通りだから、
9×9=81通り･･･（答）
図１


「重複」の読み方
　検定済み教科書3冊のうち、索引の「さ行」に重複順列と書かれているもの（=「じゅうふく」と読むもの）が1冊、索引の「た行」に重複順列と書かれているもの（=「ちょうふく」と読むもの）が1冊、両方に書かれているもの（=「じゅうふく」「ちょうふく」のどちらでもよい）が１冊でした。筆者はどちらでもよいと教えながら、口では「じゅうふく」と言います。


【重複順列において前提となっている事柄】
(1) 同じものを繰り返して使ってよい代わりに、全く使われないものもあります。
　例えば、左の例1において33は条件を満たす１つの数ですが、この数には1,2,4,5,6,7,8,9は一度も使われていません。この事情は、一般の順列のときにも当てはまります。
(2) rがnよりも大きいこともあります。
　一般の順列では、0≦r≦nでなければなりませんが、重複順列では同じものを何度でも使えますので、例えば異なる3個のものから、5個取ってくることができます。

【重複順列の落とし穴】
　重複順列の総数はnrという簡単な公式になるため、機械的に暗記するだけでできそうに見えますが、「どちらがnでどちらがrなのか、正確に見分ける勘を養わないと解けません。
例　5匹の猿に異なる6個の菓子を配る方法は何通りありますか。ただし、１個ももらえない猿がいてもよいとします。
56それとも65 、どちらが正しいか？
　（筆者としては、ここで「あれ〜？ん〜？」と立ち往生する方がより深い理解のためになると考えています。
下記の例4参照）
【例2】
　異なる3個の文字a,b,cから重複を許して4個取って並べる順列の総数は何通りありますか。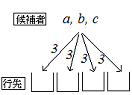
（解答）
　先頭の文字の決め方は3通り
　その各々について2番目の文字は先頭の文字と無関係に決められるから3通りの決め方がある。
　3番目、4番目の文字も同様に3通りの決め方がある。 　
以上により、3×3×3×3=81通り･･･（答）
【例3】
　二進数は、2種類の記号0 , 1を並べて表現されます。
　2種類の記号0 , 1を合計3個使って作れる記号は何通りありますか。ただし、全く使われない数字があってもよいものとします。
「3桁の二進数」といえば、001のように先頭に0が来るものを「何桁の二進数」と数えるかを決めておかなければなりませんが、ここでは「合計3個」の記号を使うとしているので、001なども3個使ったものと数えます。
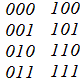（解答）
　先頭の数の決め方は2通り
　その各々について、2つ目の数の決め方も2通り
　その各々について、3つ目の数の決め方も2通り
23=8通り･･･（答）
【例4】
　5匹の猿に異なる6個の菓子を配る方法は何通りありますか。ただし、１個ももらえない猿がいてもよいとします。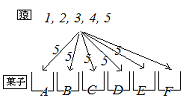
（解答）
　各々の菓子を与えるときに猿の名前を呼ぶことにします。
　名前を呼ばれた猿はその菓子をもらい、一度も名前を呼ばれない猿がいてもよいことにします。
　各々の菓子を配るときに、前の菓子の配り方と無関係に猿の名前の呼び方は5通りあるから
56=15625通り･･･（答）
※　もし、「異なる6個の菓子から重複を許して5つ取る」と考えると、配られない菓子があることになります。
（異なる5匹の猿の名刺を、重複を許して6個の菓子に貼る方法と同じになります･･･猿の面目丸つぶれです。）

【例5】
　「りんご」「かき」「みかん」各1個、合計3個の果物を、A, Bの2つの箱に分ける方法は何通りありますか。ただし、「分けた」といえるためには、1つの箱に全部入れてはいけません。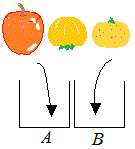
（解答）
　りんごの行先はA, Bの2通り
　かき、みかんについても同様に2通り
　これら2×2×2=8通りの中には、全部Aに入る場合が1通り、全部Bに入る場合が1通りあるから
23−2=6通り･･･（答）
※　もし、「異なる3個の果物から重複を許して2つ取る」と考えると、箱に入れない果物があることになります。
○===メニューに戻る