■ 3直線が1点で交わるための条件[例題1]3直線 2x+y−4=0 …(1) x−3y−9=0 …(2) 2x−ay+4=0 …(3) が1点で交わるように定数 a の値を定めよ. 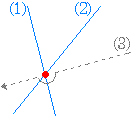 【考え方】 【考え方】3直線が1点で交わるようにするためには, (I) まず2直線の交点の座標を求める. (II) 3番目の直線が(I)で求めた交点を通るようにする. [解答1] 連立方程式(1)(2)を解いて交点の座標を求める. (1)−(2)×2 2x+ y−4=0 - )2x−6y -18=0 7y+14=0 y=−2 …(4) (4)を(1)に代入 2x−2−4=0 2x=6 x=3 よって(1)(2)の交点の座標は (3 ,−2) …(5) (5)を(3)に代入 6+2a+4=0 2a=−10 a=−5 …(答) |
[例題2] 3直線 x−ay−7=0 …(1) x + 4y+7=0 …(2) ax+2y+1=0 …(3) が1点で交わるように定数 a の値を定めよ.
【考え方】 交点の座標に文字 a が含まれていても同じようにやればよい. [解答2] 連立方程式(1)(2)を解いて交点の座標を求める. (1)−(2) x−ay−7=0 - )x +4y+7=0 (−a−4)y−14=0 (a+4)y=−14 (ア) a≠−4 のとき y=− …(4) (4)を(2)に代入 x+4(− )+7=0 x=4()−7=−7= = よって(1)(2)の交点の座標は ( , − ) …(5) (5)を(3)に代入 a( )+2(− )+1=0 a(−7a+28)−28+a+4=0 - 7a2+28a−28+a+4=0 7a2−29a+24=0 (7a−8)(a−3)=0 a= , 3 …(答) (イ) a=−4 のとき(1)(2)は平行線となるから題意に適さない. |
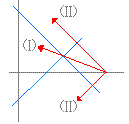 【考え方】
【考え方】