|
現在地と前後の項目 積の法則/和の法則/場合分けのまとめ方/樹形図.辞書式配列/階乗/階乗，順列/隣り合う並び方/両端指定，整数の順列/円順列，じゅず順列/重複順列/組合せ/組合せ２/組合せ３(文章題)/組分け/同じものがあるときの順列/順路/番号札のもらい方/二項定理,多項定理,二項係数の性質/約数の個数，約数の総和（入試問題）/二項定理,多項定理（入試問題）/重複組合せ/重複組合せ２(文章題)/順列・組合せ(章末問題)/ ■場合分けのまとめ方 実際に出会う問題では、積の法則や和の法則を単独で用いることは少なく、これらを組み合わせて使います。 そのとき、場合分けした「各々の場合を積の法則で処理し」「全体を和の法則でまとめる」という流れが基本です。
【例1】
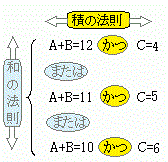
（解答）3つのさいころA、B、Cを同時に投げるとき、出た目の和が16になる場合の数は何通りありますか。 右図１のようにA+Bの和とCの表を作ると
（ア）A+Bの和が12になるのは1通り
このときCの目が4になるのは1通り A+B=12となるのは1通り
（イ）A+Bの和が11になるのは2通りその各々についてCの目が5になるのは1通り A+B=11となるのは2通り
（ウ）A+Bの和が10になるのは3通りその各々についてCの目が6になるのは1通り A+B=10となるときは3通り
（*）A+Bの和が9以下のときは、該当する場合なし以上により、1+2+3＝6通り
この問題のように、場合分けした結果は次のようにまとめます。
「細分したものを積の法則で」「全体のまとめを和の法則で」処理します。
■分かれば何でもないことですが･･･■
数学に自信をなくしている人では、上記の（ア）（イ）（ウ）の結果を、さらに「積の法則でまとめる」間違いが多く見られます。 ⇒ （ア）（イ）（ウ）のような「場合分け」は重複しないように分けているので、これらは「同時には成り立ちません」。したがって、「和の法則」を使う場面になっています。 ※ （より進んだ学習をしている人への参考） 例1の問題を「異なる3つのものA、B、Cから重複を許して16個取る組合せの総数」として解くことはできません。 重複組合せで求めると、例えばA=7、B=8、C=1のように1つの目が7以上の場合も数えることになり、不適当です。 |
図１
【例2】
図２のようにA+BとC+Dの表を作ると
4つのさいころA、B、C、Dを同時に投げるとき、出た目の和が22になる場合の数は何通りありますか。
（ア）A+Bが10になるのは3通り
このときC+Dが12になるのは1通り 3×1=3通り
（イ）A+Bが11になるのは2通りその各々についてC+Dが11になるのは2通り 2×2=4通り
（ウ）A+Bが12になるのは1通りその各々についてC+Dが10になるのは3通り 1×3=3通り
（*）A+Bが9以下のときはC+Dで該当する場合なし、A+Bが13以上のときはA+Bで該当する場合なし以上により、3+4+3＝10通り
【例3】
（解答）
Aのテーブルには大人2人と子供3人、Bのテーブルには大人3人と子供2人が席についています。AとBの間でメンバを1人すつ入れ替えるとき、各テーブルの大人・子供の人数が変わる場合は何通りありますか。
（ア）AからBへ大人が行くのが2通り
その各々についてBからAへ子供が行くのが2通り 2×2=4通り
（イ））AからBへ子供が行くのが3通りその各々についてBからAへ大人が行くのが3通り 3×3=9通り
以上により、4+9＝13通り
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
問題１３つのさいころA, B, Cを同時に投げるとき，出た目の和が15になる場合の数を求めてください．
A+B=10となるのは3通り，その各々についてC=6となるのが1通り→3×1=3通り A+B=11となるのは2通り，その各々についてC=6となるのが1通り→2×1=2通り A+B=12となるのは1通り，その各々についてC=6となるのが1通り→1×1=1通り ゆえに，10通り |
問題２4つのさいころA, B, C, Dを同時に投げるとき，出た目の和が23になる場合の数を求めてください．
A+B≦10のときは，C+D≦12だから和は23にならない A+B=11となるのは2通り，その各々についてC+D=12となるのは1通り→2×1=2通り A+B=12となるのは1通り，C+D=11となるのは2通り→1×2=2通り 結局，2+2=4通り （＜別解＞全部6が出たら目の和は24．１つだけ5で残り3個が6のとき目の和は23．５となるさいころの選び方は4通り．） |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
問題３Aの袋にはハートのカードが２枚とスペードのカードが３枚入っており，Bの袋にはハートのカードが３枚とスペードのカードが２枚入っている．Aの袋から１枚取り出してBの袋に入れ，よくかきまわしてBの袋から１枚取り出してAの袋に戻すとき，Aの袋にハートのカードが２枚とスペードのカードが３枚入っている場合の数は何通りありますか．（カードはすべて区別します．）
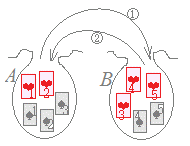Aからハートが取り出されるのが2通り，その各々についてBからハートが戻されるのが4通り→2×4=8通りAからスペードが取り出されるのが3通り，その各々についてBからスペードが戻されるのが3通り→3×3=9通り 和の法則により，8+9=17通り |
問題４袋の中に赤玉が３個，黄玉が２個，青玉が４個入っている．この中から「同時に２個」取りだしたとき，同じ色が出る場合の数は何通りありますか．
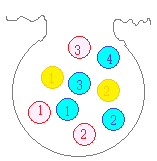赤赤となるのは，赤1-赤2，赤1-赤3，赤2-赤3の３通り黄黄となるのは，黄1-黄2の１通り 青青となるのは，青1-青2，青1-青3，青1-青4，青2-青3，青2-青4，青3-青4の6通り 和の法則により，3+1+6=10通り （ここでは単純に数えましたが，この計算は後で習う組合せを使って求めることができます．） |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||