|
【回転体の体積】
y=f(x) (a≦x≦b)とx軸とで囲まれる図形をx軸のまわりに回転して得られる回転体の体積Vは V=π f(x)2dx で求められます. 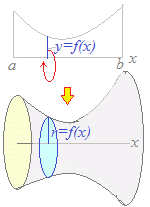
上の図のようにx軸のまわりに回転させたとき,x軸に垂直に切った断面は円になり,その半径はf(x)になります.
正確に言えば,f(x)<0のときは,r=|f(x)|になりますが,この公式では2乗して使うので,負の場合を区別する必要はありません.
したがって,断面積はS(x)=πf(x)2になり,これをa≦x≦bの区間で積分すれば,回転体の体積になります.
V=π ()2dx=π x3dx=π =π(−0)=
→ 4
|
○この頁に登場する【問題】は,公益社団法人日本技術士会のホームページに掲載されている「技術士第一次試験過去問題 共通科目A 数学」の引用です.(=公表された著作物の引用)
○【解説】は個人の試案ですが,Web教材化にあたって「問題の転記ミス」「考え方の間違い」「プログラムの作動ミス」などが含まれる場合があり得ます. 問題や解説についての質問等は,原著作者を煩わせることなく,当Web教材の作成者(<浅尾>)に対して行ってください.
平成19年度技術士第一次試験問題[共通問題]
【数学】Ⅲ-6 曲線y=cos x (−≦x≦)とx軸とで囲まれた部分を, x軸の周りに回転させて得られる回転体の体積は,次のどれか. 1 2 3 4 5 HELP
V=π cos2x dx=π dx=π +
=π{(0+)−(0−)}= → 5 |
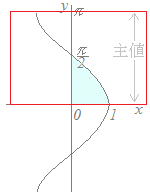 逆三角関数
逆三角関数y=cos−1x ⇔ x=cos y は,右図のように −1≦x≦1, 0≦y≦π の区間で定義されます. この区間において,x軸およびy軸とで囲まれるのは,0≦y≦の部分です. V=π x2 dy←yで積分 =π cos2y dy =π dy =π + =π{(0+)−(0+0)}= → 5 |