|
■媒介変数表示
x, y座標がそれぞれ第3の変数tを用いて
※角度を媒介変数に使うときは,媒介変数をθで表す場合も多い. |
【媒介変数表示で表される曲線・直線の調べ方】
(1) 媒介変数を消去してx, yの方程式に直す.
x, yの方程式は中学校以来なれているので,x, yの方程式に直せば分かりやすくなる場合があります.
(2) t=0,1,2などいくつかの値に対応する点を調べてみる.しかし,x, yの方程式に直せない問題も多くあります.
この方法は,原始的なもので,すべてのtの値に対して調べている訳ではないので,軽く見られがちですが,以下で述べる「散布図」の利用はこれを多数の点について行うもので,ほとんどの問題に対して有効です.
|
|
■媒介変数表示■
【サイクロイド】
【できること】 与えられた媒介変数表示から
△:tについて陽に解くこと,媒介変数tを消去してx, yだけの方程式にすること
yの表示から逆三角関数を使えば,tについて解くことができるが,高校では逆三角関数を使う表示は扱わない.
○:コンピュータを使ってグラフを描くこと

【エクセルを使ってこのグラフを描く方法】 aの値(補助円の半径)に応じて相似的に拡大されるだけなので,a=1の場合のグラフを描くと次のようになる. 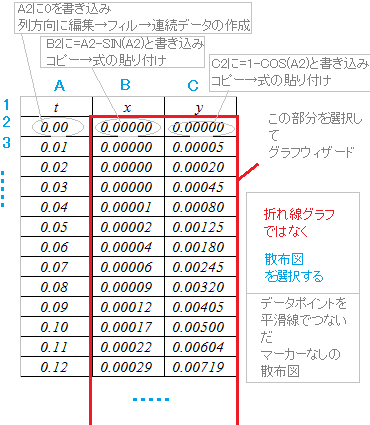 ※実際には,点の個数が100個もあれば十分正確なグラフができます.(表計算で表題+100行もあれば十分です) |
【グラフの概形】
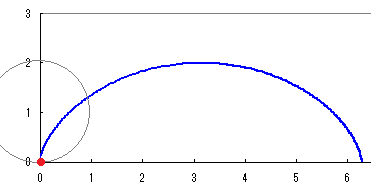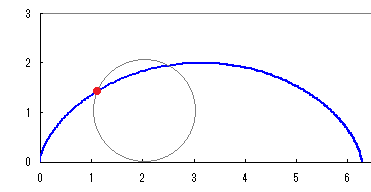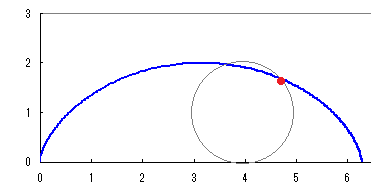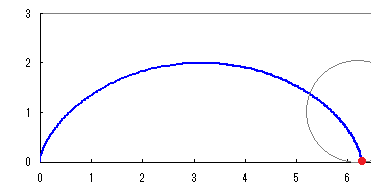  図のように円をx軸に沿って「滑らないように」回転させる.はじめ原点と重なっていた円周上の1点Pの描く軌跡を考える. 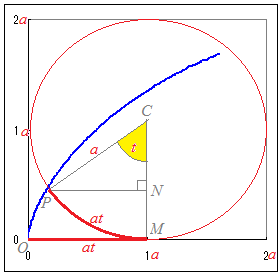 Pのx座標は
x=OM−PN=a(t)−a(sint)
Pのy座標は
y=CM−CN=a−a(cost)
※サイクロイド曲線は,最速降下曲線とも呼ばれ,初速度0で落差のある2点間を重力の力だけで転がした時に,最も速く到達できる曲線の形になっています.(上下を逆にしたサイクロイド)
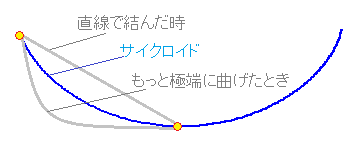 これに対して,サイクロイドのように初めを急坂にしておくと,距離は少々長くなっても,高速で進む分だけ速くなる. しかし,極端に曲げて直角に近い形にし過ぎると経路の長さが足を引っ張る. |
||
|
■媒介変数表示■
【トロコイド】
(1) 基本となるサイクロイド
 と同じ大きさの回転による速度 と同じ大きさの回転による速度 が合成されるので, が合成されるので,
○動点PがAの位置(またはCの位置)にあるときは,
 に対して逆向きの に対して逆向きの が足されるので,動点Pの速度は差し引き0となって止まる. が足されるので,動点Pの速度は差し引き0となって止まる.
○動点PがBの位置にあるときは,
 に対して同じ向きの に対して同じ向きの が足されるので,動点Pの速度は右向けに加算されます. が足されるので,動点Pの速度は右向けに加算されます.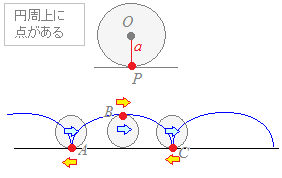
サイクロイド⇒A, Cの位置で折れ曲がっている
(2) ところが,b<aの場合には
 よりも小さな回転による速度 よりも小さな回転による速度
○動点PがAの位置(またはCの位置)にあるときは,
 に対してこれよりも小さな逆向きの に対してこれよりも小さな逆向きの
○動点PがBの位置にあるときは,
 に対してこれよりも小さな同じ向きの に対してこれよりも小さな同じ向きの
○さらに,点A,Cの位置はx軸上ではなく,これよりも上にあり,点Bの位置は円の上端よりも下に来ます.
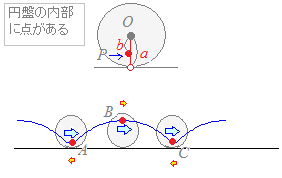
b<a⇒A, Cの位置でも右に進んでいる
|
(3) b>aの場合には
 よりも大きな回転による速度 よりも大きな回転による速度
○動点PがAの位置(またはCの位置)にあるときは,
 に対してこれよりも大きな逆向きの に対してこれよりも大きな逆向きの
○動点PがBの位置にあるときは,
 に対してこれよりも大きな同じ向きの に対してこれよりも大きな同じ向きの
○さらに,点A,Cの位置はx軸上ではなく,これよりも下にあり,点Bの位置は円の上端よりも上に来ます.
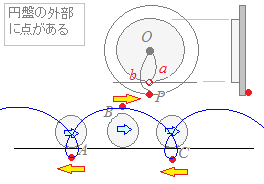
b<a⇒A, Cの位置で左向きに進み,
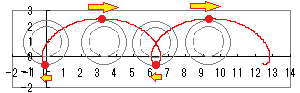
≪エクセルを使ったグラフの作成≫ループができます ※高校の授業では,通常,トロコイドまでは扱いませんが,エクセルを使えば簡単にグラフが描けます. 次のグラフは
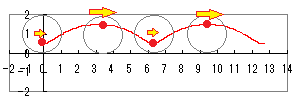 次のグラフは
 |
|
■媒介変数表示■
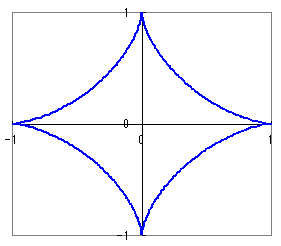
【アステロイド】(星芒形:せいぼうけい)
【できること】 与えられた媒介変数表示から
△:tについて陽に解くこと
(逆三角関数を使えば解けるが,高校では逆三角関数は扱わない.)
○:媒介変数tを消去してx, yだけの方程式にすること
=cos3t, =sin3tだから
()+()=cos2t+sin2t=1
x+y=a
○:コンピュータを使ってグラフを描くこと

kが偶数の整数の場合や,kが分母または分子が偶数となる分数の場合には,x≧0,y≧0の範囲にのみグラフがあります. kが奇数の整数の場合や,kが分母分子とも奇数の分数となる場合には,x,yが負の場合もグラフがあります.
k=1→x2+y2=1のとき円
k=2→x+y=1のとき直線(一部:線分) でkの大小に応じて図のように曲がり方が変わります. 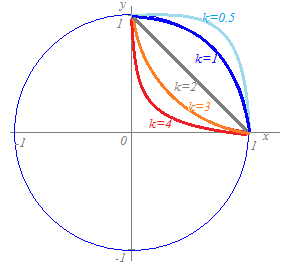
※今日の数学では,2点間の距離をユークリッドの意味(三平方の定理で求まる斜辺の長さ)だけでなく,他の定義も使われます.
一般に,原点O(0,0)と点P(x,y)の間の距離を OP(n)= と定義したとき,OP(n)=aとなる点,すなわち xn+yn=an となる点の軌跡がこれらのグラフになり,
n=2の場合は,古典的なユークリッドの意味で定義された距離で測ったときに,原点からの距離がaとなる点の軌跡は円になること
などが分かります.
n=1の場合は「直交する2辺の和|x|+|y|」として定義された距離で測ったときに,原点から距離がaとなる点の軌跡は直線になること |
【類似の図形との関係2】・・・ハイポ・サイクロイド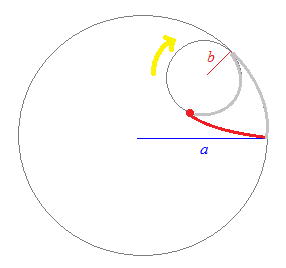 ハイポ・サイクロイドの形は,大きな円の半径aと小さな円の半径bの比率によって決まります. ≪数式の変形≫
sin3α=3sinα−4sin3α → sin3α= cos3α=4cos3α−3cosα → cos3α= を使って変形すると x=(3cosα+cos3α)=cosα+cos3α…(1') y=(3sinα−sin3α)=sinα−sin3α…(2') ≪図形的な意味≫ 図のように,大きい円の半径aとに対して,小さな円の半径b=のとき 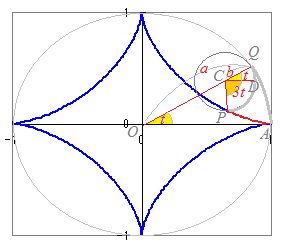 このとき,Pのx,y座標は x=cost+cos3t y=sint−sin3t (1)(1')(2)(2')により,これはアステロイドの媒介変数表示になっています. ≪一般のハイポ・サイクロイド≫ 上と同様に,一般にb=のとき
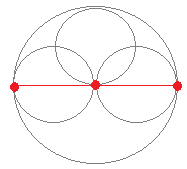 (n=2のとき)
(n=2のとき)b= x=cost+cost=acost y=sint−sint=0 ⇒ 直径になる 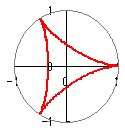 (n=3のとき)
(n=3のとき)b= x=cost+cos2t y=sint−sin2t ⇒ デルトイド 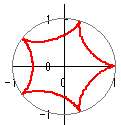 (n=5のとき)
(n=5のとき)b= x=cost+cos4t y=sint−sin4t ⇒ 尖点5個のハイポ・サイクロイド |
|
■媒介変数表示■
【エピ・サイクロイド】
≪図形的な意味≫
大きな円(半径a)の外側に小さな円(半径b)を滑ることなく転がしていくときに,小さな円の周上にある点Pの軌跡はエピ・サイクロイドと呼ばれます. 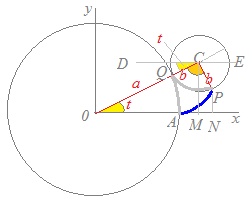
OM=(a+b)cost
次に,滑らずに転がると弧QPの長さと弧QAの長さは等しいから,中心角∠COA=tと∠PCQの比はa:bになるから ∠PCQ=t また,∠DCQ=∠QOA=tだから∠DCP=t+t=t ∠ECP=π−t MN=bcos(π−t)=−cos(t) したがって,点Pのx座標は x=(a+b)cost−cos(t) y座標についても同様にして示される. |
≪エクセルを使ったグラフの作成≫ ここまでと同様の方法でエクセルを使ってグラフを作ることができます. (a=1, b=1:2つの円が同じ大きさのとき) 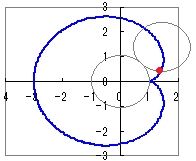
このグラフは,極座標表示で登場するカージオイド(心臓形)と一致します.(ただし,x軸方向にaだけ平行移動されています) (a=1, b=0.5:小さな円が2回転します) 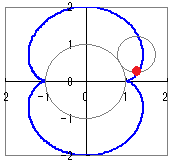
(a=1, b=1/3:小さな円が3回転します) 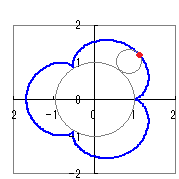
|
||||||||
|
≪軽い応用≫ サイクロイドに対するトロコイドの関係と同様にして,ハイポ・サイクロイドに対しても,角の取れた曲線やループのある曲線を考えることができます. 式だけを見ても,なかなか難しく思えますが,図形的な意味を考えるとわかります. b=に対して,円盤の内部:c<bとなる点,円盤の外部: c>bとなる点を動点に選べば
右側はa=1 , b=, c=の場合のグラフ 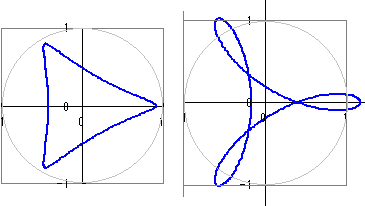 |
 式だけを見ても,なかなか難しく思えますが,図形的な意味を考えるとわかります. b=に対して,円盤の内部:c<bとなる点,円盤の外部: c>bとなる点を動点に選べば
右側はa=1 , b=, c=の場合のグラフ 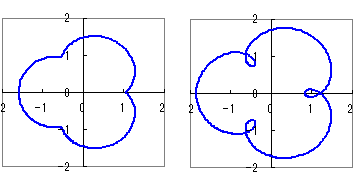 |
|
■媒介変数表示■
【インボリュート】(円の伸開線)
【できること】 与えられた媒介変数表示から
×:tについて陽に解くこと
×:媒介変数tを消去してx, yだけの方程式にすること
○:コンピュータを使ってグラフを描くこと

【エクセルを使ってこのグラフを描く方法】 aの値に応じて相似的に拡大されるだけなので,a=1の場合のグラフを描くと次のようになる. 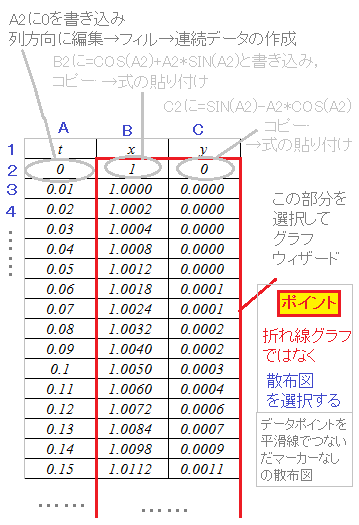 (!?)⇒コンピュータの画面は1000×1000ドット程度の解像度なので,実際上は折れ線をつないだものとなりますが,全体の特徴が分かるような範囲を選ぶことが重要 |
【グラフの概形】
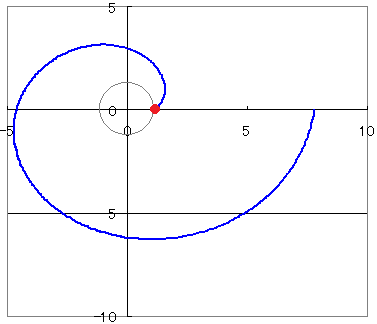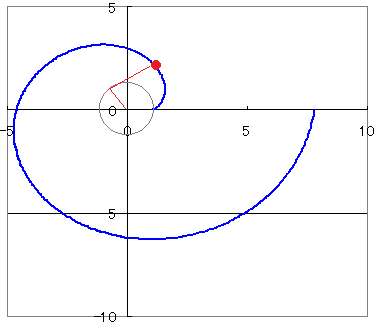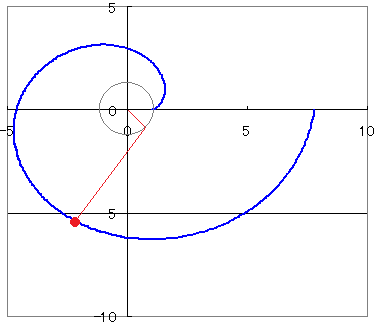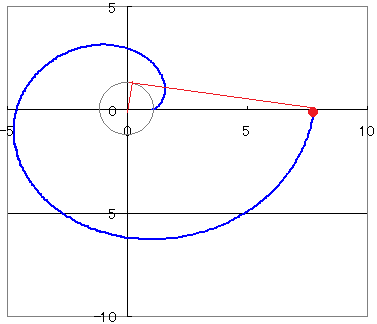 【参考:図形的な意味】 図のように,円周に巻きつけられた糸の糸口Pが円周上の1点Aに重なっているときに,この糸をたるまないように引っ張りながらほどいていくときの点Pの軌跡を考える. 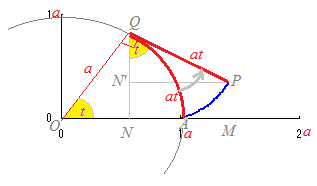 PQは接線だからPQ⊥OQ→∠PQN=∠QON=t このとき,Pのx座標は
x=ON+N'P=a(cost)+at(sint)
Pのy座標は
y=QN−QN'=a(sint)−at(cost)
※インボリュート歯車
インボリュート曲線は歯車に使われている. |
|
≪簡単チェックテスト≫
◇この頁に登場した媒介変数表示とグラフを対応させる問題です.(無理に覚える必要はなく,上の解説を読み直しながら解ければよいでしょう.)
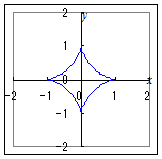
【問題1】◇はじめに左欄の媒介変数表示を1つ選び,続けて右欄のグラフを選んでください. ◇間違ったときにやり直すには,問題を選び直すことから始めてください. |
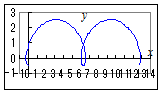 2.
2.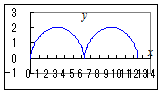 3. 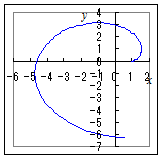 4. 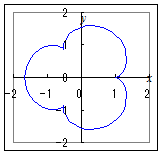 5.
5.
|
|
≪応用力テスト≫
◇全然習っていない問題でも,この頁で解説した「エクセルグラフで散布図を作る方法」が習得できれば,グラフを調べることができます.
各自でエクセルグラフの散布図を作って,次の問題に答えてください. ◇はじめに左欄の媒介変数表示を1つ選び,続けて右欄のグラフを選んでください.「この問題を解くには,1問当たり少なくとも10分程度の時間が必要です.」・・・まぐれで当たっても意味がありません. ◇間違ったときにやり直すには,問題を選び直すことから始めてください. 【問題2】
≪エクセルワークシト上の演算≫
例えばエクセルのセルA4に媒介変数tの値があるとき
○セルB4にt2−1の値を書き込むには,=A4^2-1とします.
○セルC4にt2+3tの値を書き込むには,=A4^2+3*A4とします. ○セルB4にt+の値を書き込むには, =A4+1/A4とします. ○セルB4にcos3tの値を書き込むには,=COS(3*A4)とします. ※5行目以下のセルの値は,式のコピー&貼り付けで行います. |
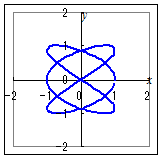 2.
2.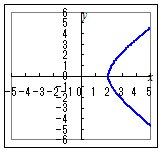 3. 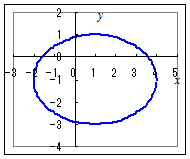  4. 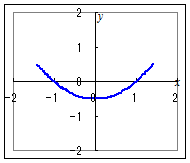 5.
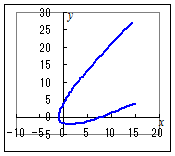
5.
|