|
【tanx, cotxに関する不定積分】
○[ dx → log|f(x)|+C]
(解説)tanx dx=−log|cosx|+C…(*4.1) cotx dx=log|sinx|+C…(*4.2) dx=−log|cosx−sinx|+C…(*4.3) dx=||+C…(*4.4) ○[(tan x)’= → =tanx] tan2x dx=tanx−x+C…(*4.5) tan3x dx=tan2x+log|cosx|+C…(*4.6) tan4x dx=tan3x−tanx+x+C…(*4.7) ○[(cot x)’=− → =−cotx] cot2x dx=−cotx−x+C…(*4.8) cot3x dx=−cot2x−log|sinx|+C…(*4.9) cot4x dx=−cot3x+cotx+x+C…(*4.10) ○[部分積分を行うもの] x tan2x dx=−x2+xtanx+log|cosx|+C…(*4.11) ○[部分積分で漸化式を作って次数を下げていくもの] In=tannx dx (n≧2)とおくと In=tann−1x−In−2…(*4.12) ※この漸化式から一般項を求めようとせずに, I0→I2→I4→... I1→I3→I5→... と順次求めるために使う. (*4.1)(*4.2)← 被積分関数の分子が分母の微分になっているとき すなわち dxの形の不定積分は f(x)=tとおく置換積分により,=f’(x) → dx= dx===log|t|+C 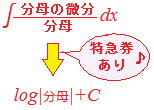 したがって
したがってdx=log|f(x)|+C となって,直ちに不定積分が求められます. これにより tanx dx=dx=−dx =−log|cosx|+C…(*4.1) cotx dx=dx=dx =log|sinx|+C…(*4.2)
※習う生徒と習わない生徒がいて,よく質問がある記号
(*4.3)←(A)〜(C)については,3文字目の逆数と覚えるとよい
(コセカントx) cosec x → 1/sin x
(セカントx) sec x → 1/cos x (コタンジェントx) cot x → 1/tan x ===− 分子が分母の微分になっているから dx=−log|cosx−sinx|+C (*4.4)← 三角関数の相互関係から 1+tan2x=だから dx=dx=Iとおく ここで,tanx=tとおく置換積分を行うと,=だから I=cos2x dt=−dt =−(−)dt=−(log|t−1|−log|t+1|)+C =−log||+C=log||+C=||+C (*4.5)← tan2x dx=dx=dx =(−1)dx=tanx−x+C (*4.6)← tan3x dx=tan2xtanx dx=(−1)tanx dx =tanxdx−tanx dx 第1項は,tanx=tとおく置換積分を行うと,=だから t cos2x dt=t dt=t2+C’=tan2x+C’ 第2項は,上記の通り−log|cosx|+C”となるから tan3x dx=tan2x+log|cosx|+C |
(*4.7)← tan4x dx=tan2x tan2x dx=tan2x(−1)dx =tan2xdx−tan2x dx 第1項は,tanx=tとおく置換積分を行うと,=だから t2cos2x dt=t2 dt=t3+C’=tan3x+C’ 第2項は,上記の通りtanx−x+C”となるから tan4x dx=tan3x−tanx+x+C (*4.8)← cot2x dx=dx=dx =(−1)dx=−cotx−x+C (*4.9)← cot3x dx=cot2xcotx dx=(−1)cotx dx =cotxdx−cotx dx 第1項は,cotx=tとおく置換積分を行うと,=−だから −t sin2x dx=−t dt=−t2+C’=−cot2x+C’ 第2項は,上記の通り−log|sinx|+C”となるから cot3x dx=−cot2x−log|sinx|+C (*4.10)← cot4x dx=cot2x cot2x dx=cot2x(−1)dx =cot2xdx−cot2x dx 第1項は,cotx=tとおく置換積分を行うと,=−だから −t2sin2x dt=−t2 dt=−t3+C’=−cot3x+C’ 第2項は,上記の通り−cotx−x+C”となるから cot4x dx=−cot3x+cotx+x+C (*4.11)← x tan2x dx=Iとおく
=xtanx−x2−tanx+x2 上記の(*4.1)の結果から tanx dx=−log|cosx|+Cだから I=−x2+xtanx+log|cosx|+C (*4.12)← In=tannx dx=tann−2x tan2x dx =tann−2x(−1)dx=tann−2xdx−In−2 第1項は,tanx=tとおく置換積分を行うと,=だから tn−2cos2x dt =tn−2 dt=tn−1+C=tann−1x+C となるから In=tann−1x−In−2 [例]
I0=tan0x dx= dx=x+C
I2=tan1x−I0=tanx−x+C
I4=tan3x−I2=tan3x−(tanx−x)+C
=tan3x−tanx+x+C
I1=tan1x dx=−log|cosx|+C
I3=tan2x−I1=tan2x+log|cosx|+C
I5=tan4x−I3=tan4x−(tan2x+log|cosx|)+C
=tan4x−tan2x−log|cosx|+C
なお,負の値に対して,I−n=tan−nx dx=cotnx dx=Jnを求めるためには,この漸化式を逆向きに使えばよい.上記の証明は,n<0のときでも成り立つから.(ただし,ここでは負の指数は逆三角関数ではなく,逆数(分数)を表すものとする) In=tann−1x−In−2 から In−2=tann−1x−In In=tann+1x−In+2 だから Jn=I−n=tan−n+1x−I−n+2=cotn−1x−Jn−2 [例]
J0=cot0x dx= dx=x+C
J2=−cotx−J0=−cotx−x+C…(*4.8)
J4=−cot3x−J2=−cot3x+cotx+x+C…(*4.10)
J1=cotx dx=log|sinx|+C…(*4.2)
J3=−cot2x−J1=−cot2x−log|sinx|+C…(*4.9)
J5=−cot4x−J3=−cot4x+cot2x+log|sinx|+C
|
||||
|
以下の問題は,この頁のどこかに書かれている内容か,または,それを少しだけ変形したものです.正しい番号を選択してください.
=tとおくと,= → dx=2 dtとなるから tan2 dx=tan2t·2·dt=2tan2t dt …(*4.3)により
=2(tant−t)+C=2(tan−)+C=2tan−x+C→2
|
=tとおくと,= → dx=3 dtとなるから tan dx=tant·3·dt …(*4.1)により
=3(−log|cost|)+C=−3log|cos|+C→3
|
||||
|
…(*4.2)
→1
|
…(*4.9)
→2
|
||||
|
…(*4.4)
→3
|
2x=tとおくと,=2 → dx=となるから cot2x dx=cott =cott dt …(*4.2)
=log|sint|+C=log|sin2x|+C→4
|
||||
|
[問題7]
次の不定積分を求めてください. x tan2x dx 1tan3x−x tan2x+x2tanx+C 22xtan3x+tan2x+2xtanx+C 3x2−xtanx−log|sinx|+C 4−x2+xtanx+log|cosx|+C HELP
…(*4.11)
→4
|
…(*4.7)
→1
|
||||
|
…(*4.12)においてn=4を代入します.
→3
|
[問題10]
Jn=cotnx dxとおくとき, 次のどの漸化式が成り立ちますか. 1J5=cot4x−J3 2J5=−cot4x−J3 3J5=cot5x−J4 4J5=−cot5x−J4 HELP
…(*4.12)解説参照 n=5を代入します.
→2
|