��ԍ��W�C��ԃx�N�g��--�����Ɨ��
�@���̃y�[�W�́C��ԍ��W���ԃx�N�g���̊�{�������L�����グ�C���ɊȒP�ȗ������������̂ł��D
�@���̕����́C���ȏ�����Ƃł́C���ʍ��W�E���ʃx�N�g���Ɠ��e�I�ɏd�Ȃ邱�Ƃ������C��ԍ��W�E��ԃx�N�g���̕�����S�������邱�Ƃ͂܂�Ȃ̂ŁC�K�v�ƂȂ����Ƃ��Ɏg���₷���`�ňꗗ�I�Ȃ��̂�������D
�y2�_�Ԃ̋����z
�y���P�z�@����2�_�Ԃ̋��������߂Ă��������D�@2�_ �@���ɁC���_
(1)
�i�j�@ (2) �@ (1) (2) �y���Q�z
(1)
�i�j�@x����ɂ����āC�Q�_ (2) �@xy���ʏ�ɂ����āC�R�_ (1)
x����̓_��P(x, 0, 0)�ȂǂƂ�����Dy���W��z���W��0�ɂȂ�Ƃ��낪�|�C���g
���߂�_��P(x, 0, 0)�Ƃ������Q��̌`�ɂ���ƁC�����Ȃ��Ōv�Z�ł��� |
(2)
xy���ʏ�̓_��Q(x, y, 0)�ȂǂƂ�����Dz���W��0�ɂȂ�Ƃ��낪�|�C���g
���߂�_��Q(x, y, 0)�Ƃ�����
����ɂ����
�Q��̌`�ɂ���ƁC�����Ȃ��Ōv�Z�ł����������Ƃ��Ă� �̂ǂꂩ���g�� ���������ËL���������ł͖��͉����Ȃ� �@)���� �A)���� �@’),�A’)����
���̖��ł́C�u�Q�_���瓙�����ɂ���v�Ƃ������������ł͉����Ȃ��D�u�R�_���瓙�����ɂ���v�Ƃ��������ɂ���āC���m���Q�̘A���������ɂȂ��ĉ�����D
�u�S�_���瓙�����ɂ���v�Ƃ��������ɂȂ��Ă��C��ʂɂ͉����Ȃ�…���m���Q�ŕ��������R�ɂȂ邩�� |
|
�y�O�p�`�̌`����z �@2�_�Ԃ̋����̌����Ɋ֘A���āC�O�p�`�̌`���肪�o����邱�Ƃ�����D����́C�O�p�`ABC�̒��_�̍��W���^����ꂽ�Ƃ��ɁC���̎O�p�`���ǂ̂悤�Ȍ`�̎O�p�`�ł��邩������̂ŁC�O��AB, BC, CA�̒��������炩���ߌv�Z���Ă����C���̂ǂ̌^�ɓ��Ă͂܂邩����D
(1) AB=BC�ȂǂƂȂ����Ƃ�
→ �uAB=BC�̓ӎO�p�`�v�ȂǂƓ�����
�P�Ɂu�ӎO�p�`�v�Ɠ������ꍇ�ɂ́C�ǂ̂Q�g�̕ӂ�����������������Ă��Ȃ��̂ŁC���_�ɂ���̂����ʂł�
(2) AB=BC=CA=3�ȂǂƂȂ����Ƃ�→ �u��ӂ̒�����3�̐��O�p�`�v�ȂǂƓ�����
�P�Ɂu���O�p�`�v�Ɠ����Ă��l�X�ȑ傫��������̂ŁC1�ӂ̒�����������ꍇ�ɂ́C����������ׂ����ƍ̓_���͍l���܂�
|
(3) AB2+BC2=CA2�ȂǂƂȂ����Ƃ�
(��)�O�ӂ̒����݂̂���|����ɂ��ĎO�p�`�̌`������߂���ł́C�u��A=120���̎O�p�`�v�̂悤�Ȍ`�̓����͏o�Ȃ��̂����ʂł��D→ �u��B=90���̒��p�O�p�`�v�ȂǂƓ�����
�@�ӂ̒�����������|����ɎO�p�`�̌`������߂�Ƃ��ɁC���p�Ƃ����p�x�̐������q�ׂ邱�Ƃ��ł���̂́C�O�����̒藝�̋t���璼�p�O�p�`��������ꍇ�ł��D
(4) AB2+BC2=CA2�CAB=BC�ȂǂƂȂ����Ƃ��@����ɓ��Ă͂܂邩�ǂ����́C�Q��̘a�������ɋ��߂Ă݂Ȃ��ƕ�����܂���D �@�P�Ɂu���p�O�p�`�v�Ɠ�����̂ł͂Ȃ��C�ǂ̊p�����p�����q�ׂȂ���Ȃ�܂���D�i�Œ��̕�=�Εӂɓo�ꂵ�Ȃ����_�����p�ł��D�������́C2��̘a��2��o�ꂷ�钸�_�����p�ł��j → �u��B=90���̒��p�ӎO�p�`�v�ȂǂƓ�����
�@���p�O�p�`�ƓӎO�p�`�̗�����������ꍇ�ł��D
�@�������Ƃ��ẮC���p�̊p���ӂ̕ӂ̑g�������ꂩ�������悤�ɂ��܂� �@�ӂ̒�����������|����ɂ����ꍇ�ɁC�����I�Ɋp�x�̐�������������̂́C�O�����̒藝�̋t���g�����p�O�p�`�i90���j�ƎO�ӂ̒������������ꍇ�̐��O�p�`�i60���j���炢�̂��̂ŁC����ȊO�͒����p���ɂȂ�܂��D |
|
�y���R�z�@���̂R�_�_�Ƃ���O�p�`�͂ǂ̂悤�Ȍ`�̎O�p�`�������Ă��������D
(1)
�@ (2) �@
• �Ƃ肠�����R�ӂ̒������v�Z���Ă݂Ȃ���C�肪���肪���߂܂���D
�i�j• �ӎO�p�`��O�p�`�ͤ�ӂ̒������u���������Łv������܂����C���p�O�p�`�́u�Q��𑫂��Ă݂Ȃ��Ɓv������܂���D�����ɂ���Ă݂�Ƃ����p�����d�v�ł� (1) �䂦�ɁCAB=BC�̓ӎO�p�`…�i���j (2) ��A=90���̒��p�O�p�`…�i���j
�Ȃ��킩��̂��H �҂��Ă��Ă������͂���ė��Ȃ��D�����ɑ����Ă݂�ƁC29+22=51�ɂȂ�
|
�y���S�z�@�R�̒��_�̍��W��
�i2014�N�x�H�w�@��������j
�l�����͊ȒP�����C�v�Z�͑�ρI1�肾����30���قǂ����肻���ŁC���C�����������I
�i�j������ ���̘A�������������� (1)−(2) (2)−(3) (4)(5)���C (4)(5)�ɖ߂��� |
|
�y�����_,�O���_�̍��W�z
�y�����_�z
�@2�_ �y���_�z �@2�_ �y�O���_�z �@2�_ �y�O�p�`�̏d�S�z �@3�_ |
 �y�����_�z�̌����F��ؖ���
�y�����_�z�̌����F��ؖ�������𐬕��ɕ�����ƌ����������� |
|
�y�����_�z�̌����F���������� �@�����_�̌����Ōv�Z����Ƃ��́C�u�����W�Ƃ����W���炘���W�����߂܂��v�u�����W�Ƃ����W���炙���W�����߂܂��v�u�����W�Ƃ����W���炚���W�����߂܂��v→��ɍ������Ă͂����܂���D �@���̂悤�ɕ����Čv�Z���Ă���C��ō��W�̑g�ɂ�������C�u���₷���v�u�ԈႢ�ɂ����v�ƍl����l�͂���ł����̂ł��D 
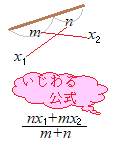 �@���������̕��q�ł́C���W
�@���������̕��q�ł́C���W�@�����W�C�����W�����l�ł��D |
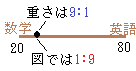 ���d���ςƂ̂������
���d���ςƂ̂�������Ⴆ�C���Ȍn�̊w�Z�ŁC���w�̓��_���d�����āC���w�Ɖp��̓������_��9:1�̔䗦�ʼn��d���ς���ꍇ�i���ۂɂ͂Ȃ��F������Ղ����邽�߂̗�j
���w�~0.9+�p��~0.1
�ƂȂ�_���́C��������ɐ��w�̓_��(�Ⴆ��20�_)�Ɖp��̓_��(�Ⴆ��80�_)��}�������ꍇ�C�^�����͂邩�ɐ��w���Ɋ�����C1:9�̔䗦�ɓ�������_�ɂȂ�܂��D=���w�~ �@���̂悤�ɁC���v�ł悭�g������d���ς̏ꍇ�C�����_�͏d������Ă�����̂ɋ߂��ꏊ�ɂȂ�܂��D �y���_�z�̌����F���������� �@���_�̍��W��\�������́C�����_�̌����ɂ����āC1�F1�ɓ�������_�����߂����̂ł��D |
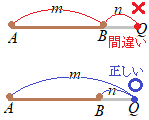 �y�O���_�z�̌����F����������
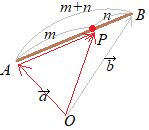
�y�O���_�z�̌����F�����������@�O���_���l����Ƃ��ɁC���Z���ɂ悭����ԈႢ�́C�E�}�́~��Ŏ������}��m:n�̔䗦���l���Ă��܂����Ƃł��D �@�������́C�E�}�́���Ŏ������悤��m:n�𑪂�Ƃ��ɁC�u����̑��͕K��Q��ł��Ȃ���Ȃ�Ȃ��v�D 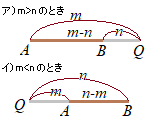 �y�O���_�z�̌����F��ؖ���
�y�O���_�z�̌����F��ؖ����A) m>n�̂Ƃ��C�O���_�͉E�}�̂悤��B�̊O�ɂ��邩�� �C) m<n�̂Ƃ��C�O���_��A�̍��ɂ��邩�� 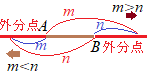 ���O���ł́Cm=n�Ƃ����ꍇ�͂Ȃ����Ƃɒ��ӁD���Ȃ킿m, n>0�ł������C�ǂ̂悤�Ȕ䗦�̓����ł����邪�C�O���ł�1�F1�̊O�������͂Ȃ��D
���O���ł́Cm=n�Ƃ����ꍇ�͂Ȃ����Ƃɒ��ӁD���Ȃ킿m, n>0�ł������C�ǂ̂悤�Ȕ䗦�̓����ł����邪�C�O���ł�1�F1�̊O�������͂Ȃ��Dm>n�Ȃ�B�̊O�ɂ���Cm<n�Ȃ�A�̊O�ɂ��邩��C�O���_��m��n�̔䂪�������_�͂Ȃ��D ���̂��Ƃ́C�O��������m=n�̏ꍇ�ɕ��ꂪ0�ɂȂ��ăG���[�ɂȂ邱�Ƃ�����m���߂���D |
�@�O���_�̌����́C�����_�̌����ɂ����āC�um��n�̂ǂ��炩����̕��������ɂ������́v�ł��D �̎��̕���ƕ��q�̗����� −1 ���|����� (1)��(2)�́C�����Ƃ��Ă͑S�������l�ɂȂ�̂ŁC�ǂ�����g���Ă��悢�D������C�um��n�̂ǂ��炩����̕��������ɂ������́v�Ƃ����܂��D �@���w�̋��t�ɂ���ẮC�u�ǂ��炩�v�Ƃ����悤�ȕs����ȕ\���ł́C���w�̎ア���k�������Ă��܂�����C�u���ꂪ�������v�ƌ��߂������悢�ƍl����l�����܂��D�Ⴆ�C�um��n�̑傫�������v���X�ɂ��āC�����������}�C�i�X�ɂ���v�Ƃ���������������܂��D���̂����ł́u���ꂪ�K�����ɂȂ邩��v�v�Z�ԈႢ������Ƃ������Ƃł��D �@�Ȃ��Cm��n�̂Q�Ƃ����ɂ���Ɠ��������ɖ߂��Ă��܂��̂ŁC�v���Ⴂ���Ȃ��悤�ɁD �����ǂǂ�Ŋo������悢���F�um��n�̂ǂ��炩����̕��������ɂ������́v�um��n�̑傫�������v���X�ɂ��āC�����������}�C�i�X�ɂ���v�Ȃǎ����̈�Ԃ������肷��̂��o������悢�̂ł����C�u�P���Ɏ��̎������̂܂܊o����v���@���ĊO�X�b�L�����܂�
�����邮�����āC���̌����ɖ߂��������Ȃ�C���߂��猾���ȂƎv���Ă͂����Ȃ�…���낢��o��������C���������̓I�Ɍ�����悤�ɂȂ�̂ł��D�����Y��邱�Ƃ͂Ȃ��ł��傤�D
|
|
�y�O�p�`�̏d�S�z�̌����F���������� �@���ʏ�̎O�p�`�̏d�S�ɂ��ẮC���̃y�[�W�ɏ����Ă��܂����C�ȉ��ɋ�Ԃ̎O�p�`�ł������Ȃ̂ŁC�v�_���Čf���܂��D 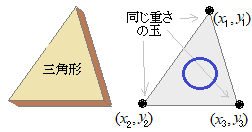 �@���������O�p�`�̏d�S�Ƃ����p�ꂪ�g���Ă��܂����C���̌������\���Ă���̂́C�d�����������_���R���_�ɂ���Ƃ��̂R�̏d���̏d�S�ł��D
�@���������O�p�`�̏d�S�Ƃ����p�ꂪ�g���Ă��܂����C���̌������\���Ă���̂́C�d�����������_���R���_�ɂ���Ƃ��̂R�̏d���̏d�S�ł��D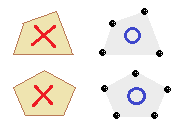 �@�O�p�`�̏ꍇ�����C�R�_�̏d�S�ƎO�p�`�̏d�S���u���܂��܈�v�v���܂����C�l�p�`�ł͂S���_�ɓ������d���̏d���u�����Ƃ��̎��_�n�̏d�S�Ǝl�p�`�̏d�S�Ƃ́C��ʂɂ͈�v���܂���D�T�p�`�ȏ�������ł��D
�@�O�p�`�̏ꍇ�����C�R�_�̏d�S�ƎO�p�`�̏d�S���u���܂��܈�v�v���܂����C�l�p�`�ł͂S���_�ɓ������d���̏d���u�����Ƃ��̎��_�n�̏d�S�Ǝl�p�`�̏d�S�Ƃ́C��ʂɂ͈�v���܂���D�T�p�`�ȏ�������ł��D�@���������� �R�̏ꍇ���� �́C�u�R�_�̏d�S�v�Ɓu�O�p�`�̏d�S�v��\���܂��� �� �͎l�p�`��܊p�`�̏d�S�̍��W��\���Ă���̂ł͂Ȃ��C�S�_�̏d�S,�T�_�̏d�S��\���Ă��邱�Ƃɒ��ӂ��Ă��������D�i��̐}�̉E���ɑΉ��j |
 �y�O�p�`�̏d�S�z�̌����F��ؖ���
�y�O�p�`�̏d�S�z�̌����F��ؖ����@�O�p�`�́u�d�S�v�Ƃ������O���t���Ă��āC�O�p�`�����͉E�̂悤�ɏd�����W�܂�_�ƈ�v���܂����C�����̏ؖ��ɂ͖ʐϑf�ӂ��d���̏W�v�͂��܂���D 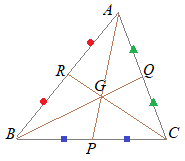 �@���������C�O�p�`�̏d�S�Ƃ́C�u�O�p�`�̂R�̒����������_�v�Ƃ��Đ}�`�I�ɒ�`����āC���̒�`���g���܂��D
�@���������C�O�p�`�̏d�S�Ƃ́C�u�O�p�`�̂R�̒����������_�v�Ƃ��Đ}�`�I�ɒ�`����āC���̒�`���g���܂��D�@���m�Ɍ����ƁC�u�R�̒����̌�_�����߂�v�v�Z�́C����������Ԃ�������̂ŁC�����ƊȒP�Ɂu�R�����̌�_�̐����v���g���܂��D 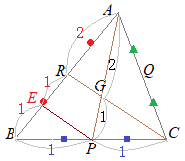 �@�E�}�̂悤�ɂR�����̌�_��G�Ƃ����Ƃ��C���w�Z�ŏK�����s���̐����ɂ��CAG:GP=2:1�ɂȂ�܂��D
�@�E�}�̂悤�ɂR�����̌�_��G�Ƃ����Ƃ��C���w�Z�ŏK�����s���̐����ɂ��CAG:GP=2:1�ɂȂ�܂��D�@�O�p�` �@���ɁCAP��2�F1�ɓ�������_�̍��W�� |
|
�y���T�z
(1) (2) �Q�_ (3) �Q�_ (4) �R�_ |
�i�j (1) (2) (3) (4) |
|
�y�x�N�g���̐}�`�ւ̉��p�z
�y�R�_���P������ɂ��邽�߂̏����z�i���������j
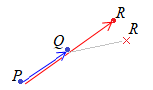 �@
�@
�R�_
�y���U�z
�i�j�@�R�_ ���̘A����������������
�y���V�z
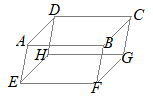 (1) ���s�U�ʑ�ABCD-EFGH�ɂ����ā�BDE�̏d�S��
(1) ���s�U�ʑ�ABCD-EFGH�ɂ����ā�BDE�̏d�S��(2) AB�̒��_��M�Ƃ���Ƃ��C3�_ (3) FG�̒��_��N�Ƃ���Ƃ��C3�_
�Ȃ��C���O������킵���ł����CG�͏d�S��\���Ă���킯�ł͂���܂���D
|
�i�j (1) ������ ���������āC3�_ �܂� ������ ���������āC3�_ �ȏォ��,�S�_ (2) ������ ����� ���������āC3�_ (3) ������ ����� ���������āC3�_ |
|
�y�x�N�g���̐}�`�ւ̉��p�z
�y�S�_�����ꕽ�ʏ�ɂ��邽�߂̏����z…(*1)
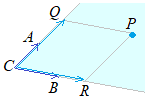 �@�_P����ABC�Ɠ��ꕽ�ʂɂ��邽�߂̏�����
�@�_P����ABC�Ɠ��ꕽ�ʂɂ��邽�߂̏������i |
�y���W�z
�i�j�@�S�_ �Ȃǂł��悢���C�ȉ��̓��Ă� ���̘A�������������� |
|
�y�x�N�g���̐}�`�ւ̉��p�z
�y�S�_�����ꕽ�ʏ�ɂ��邽�߂̏����z…(*2)
�@�P������ɂȂ��R�_ (1) �i (2) �i |
�O�q(*1)�́y�S�_�����ꕽ�ʏ�ɂ��邽�߂̏����z���g���C(1)�͎��̂悤�Ɏ������D ������ (2)�͎��̂悤�Ɏ����� �Ə����邩��CP��DC��u:(s+t)�ɓ�������_�ƂȂ�C��ABC�̓����ɂ���D |