|
== 循環小数の計算 == 《 解説 》 ■同じ数字だけが繰り返し現れる小数を循環小数といいます. 一つの数字が繰り返されるときは,その数字の上のドット(・)を付けて表わします. 二つ以上の数字のかたまりが循環しているときは,循環する数字の両端(だけ)にドット(・)を付けます.  ■循環しない部分(先頭部分だけ)と循環する部分があるとき,小数の循環する部分について循環する数字の両端(だけ)にドット(・)を付けます.(上の例のように循環する小数だけからなるものを純循環小数,この例のように循環しない部分と循環する部分からなるものを混循環小数ということがあります.)  ■循環小数は,無限等比級数の和の考え方で分数に直すことができます. <例1> 0.111111・・・・ = 0.1+0.01+0.001+0.0001+・・・ は,初項0.1,公比0.1の無限等比級数だから, 和は, <例2> 0.565656・・・ = 0.56+0.0056+0.000056+・・・ は,初項0.56,公比0.01の無限等比級数だから, 和は, ※ 公式を作ることもできますが,覚えるほどのものでもないでしょう.
■循環小数の和差積商は,分数を経由して循環小数に直すことができます. 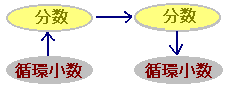 次の値を循環小数で表わしなさい. 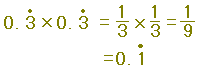 (最後のところで,分数を小数に直すには,割り算によります.) (最後のところで,分数を小数に直すには,割り算によります.)
(参考) 1=0.9999・・・ です.同様にして,2=1.99999・・・です. このようにして,(0以外の)すべての有限小数は,有限小数による表記と循環小数による表記の二つの表記法を持ちます.むしろ無限小数の表記法にそろえれば,有理数、無理数のいずれも末尾に0が並ばない無限小数でただ一通りに表わされることになります.(0だけは末尾に0が並びます.)これにより,すべての桁が同じ小数は同一の数を表わし,一つの桁でも異なるときは異なる数を表わすことになります. 循環しない無限小数(=無理数),循環する無限小数(=有理数)いずれの場合でも,すべての位の数が確定すれば,それは一つの数を表わすのは自明あって,そのような数が存在することの証明を高校生に要求するのは酷でしょう.(たとえば, 0.101001000100001000001・・・は循環しない無限小数だから,無理数です.しかし,これが「数」であることの証明は必要か?) そこで,次のような答案を私は正解にしますが,他の先生なら”収束することが証明されていない”という観点から(誤答とはしないまでも)減点の対象とするかもしれませんので,お勧めはしません.
(小話) どこかの修学旅行で、バスの中で誰かが出したクイズ: 次の記号はある人の仕事を表わしています。何の仕事でしょう?出題者の解答は「ほぼ3」→「保母さん」でしたが、数学的には、「2.999」は「ほぼ3」ですが、「2.999・・・」は「正確に3」「きっちり3」「ちょうど3」でしょう。場がしらけるといけないので黙っていましたが、「・・・」を付けると無限小数になるので、「・・・」なしで出題すべきです。 |
 右図に示すように,有理数(整数÷整数の分数)であるか無理数であるかの区別は,有限小数になるか無限小数になるかの区別には関係ありません.
右図に示すように,有理数(整数÷整数の分数)であるか無理数であるかの区別は,有限小数になるか無限小数になるかの区別には関係ありません.