|
■条件付き確率 ■ 全事象のどの要素が起こることも「同様に確からしい」とき, 事象Aの起こる確率P(A)は,「全体に対する部分の比」で定義されます。 ■ これに対して,
 |
全体集合Uの要素の個数をn(U),集合Aの要素の個数をn(A)で表わすとき,確率は全体に対する比になります。
 条件付き確率は部分に対する比になります。  |
| 【例1】 〜個数が見える例〜
あるクラス40人の生徒の男女別、芸術選択科目の人数は右図の通りであった。この中から1人を抽出して芸術選択科目を尋ねる場合、抽出されたのが女子であったとき、その女子が音楽を選択している確率 女子の人数 n(A)=21 |
 |
| 【例2】
〜時間の経過に沿って確率が絞り込まれると考えると分かりやすい例〜 5本のくじの中に当りくじが2本入っている。このくじをA,Bの順に引き,引いたくじは戻さない場合,Aが当たったときにBも当たる確率 ◎(考え方1) ※参考:Bが当たる確率 Aが当たってBも当たる確率+AがはずれてBが当たる確率 |
  |
| 【例3】 〜時間をさかのぼって原因を考える例〜
病気(かぜなど)に罹った人100人に協力してもらって、ある薬(かぜ薬など)を服用した人、服用しなかった人に分かれて、1日以内に症状の改善が見られたかどうかをテストしたとき、右のような結果が得られたものとする。(数字は、説明のために作ったものです。) 1日以内に症状の改善が見られた人を選んだとき、その人が薬を服用していた確率 1日以内に症状の改善が見られた:A、その薬を服用した:Bとする。 |

※ 確率は未来に向かって投げかけられた可能性と考えるのが自然ですが、確率、条件付き確率は「集合の要素数の比」で定義されており時間は含まれていません。だから、この例のように、内容的に過去にさかのぼっている確率もあります。(このような確率は「原因の確率」と呼ばれます.) |


 「2人とも男子ということはない」ということで,右図の黄色で示した3つの場合で考えます。このうち2人とも女子である場合は1通りです。
「2人とも男子ということはない」ということで,右図の黄色で示した3つの場合で考えます。このうち2人とも女子である場合は1通りです。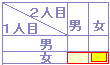 玄関から出てきたという事柄は、生まれたというのと同じように考えることができます。
玄関から出てきたという事柄は、生まれたというのと同じように考えることができます。
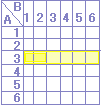 右図の通りAが3であるとき,Bが1または2となるのは
右図の通りAが3であるとき,Bが1または2となるのは 右図のようにAが勝つ15通りのうちで,Aが3を出して勝つのは2通りあるから
右図のようにAが勝つ15通りのうちで,Aが3を出して勝つのは2通りあるから ある高校の学園祭で、A組の演劇のパンフレットを見た生徒と実際にA組の演劇に来た生徒の割合は、次のとおりであった。A組の演劇に来た生徒を1人抽出したとき、その生徒がパンフレットを見た確率を求めよ.
ある高校の学園祭で、A組の演劇のパンフレットを見た生徒と実際にA組の演劇に来た生徒の割合は、次のとおりであった。A組の演劇に来た生徒を1人抽出したとき、その生徒がパンフレットを見た確率を求めよ. あるクラスでAというテレビ番組とBというテレビ番組について、見たかどうかを調査したところ、両方とも見た生徒は20%、Aだけ見た生徒は10%、Bだけ見た生徒は40%、どちらも見なかった生徒は30%であった。Aを見なかった生徒を1人抽出したとき、その生徒がBを見た確率を求めよ.
あるクラスでAというテレビ番組とBというテレビ番組について、見たかどうかを調査したところ、両方とも見た生徒は20%、Aだけ見た生徒は10%、Bだけ見た生徒は40%、どちらも見なかった生徒は30%であった。Aを見なかった生徒を1人抽出したとき、その生徒がBを見た確率を求めよ.