�@�ŏI�I�ɂ́C�\6.2�̂悤�ȃN���X�W�v�\�ɂȂ邪�C�r���o�߂ɂ͒��ӂ��ׂ��_���������D
-�y�\6.3�z-
| �� | �� |
| 61.968 | 63.298 |
| 61.747 | 80.549 |
| 61.994 | 64.535 |
| 63.052 | 73.883 |
| 62.904 | 68.557 |
| ��� | ��� |
| 63.827 | 64.417 |
(1)�@1����10�܂ł̐����Ƃ����悤�Ȑ����̏ꍇ�́C100�����Ă�10��ނ̒l�����o�ꂵ�Ȃ��̂ɑ��āC�����i�����j�̔�r�ł́C�����Ƃ��āu�Q�̎������������v�Ƃ������Ƃ͋N����Ȃ��D
�@������C�E�̕\6.3�̂悤�Ȏ����i�����j�m��ʕ\���̓s���ŏ�����3�ʂ܂ŕ\�����Ă���n�̑g���C�Ⴆ��100�g����C�����Ƃ���,x��y��100��ނ̈قȂ�l�ɂȂ�Ƒz�肵�Ȃ���Ȃ�Ȃ��D���̂��߁C�\6.3�̃f�[�^����s�{�b�g�e�[�u�����g���ăN���X�W�v�\���쐬����ƁC1���I�Ƃ͂���100�~100�ʂ�̕\�ɂȂ�D
�@�W�v���闧�ꂩ�猾���C���̂悤�Ȗ��ʂɏڂ����\��]��ł���킯�ł͂Ȃ��̂ŁC�\6.2�̂悤�ɁCx�ɂ��Ă��Cy�ɂ��Ă��K���ȕ��Łu�O���[�v�����v���Č��ʂ��W�v����D
-�y�\6.4�z-
| ���v / �� | �� |
| �� | 60.8 | 62.2 | 62.6 | 62.8 | 63.0 | 63.4 | ��� | 63.8 |
| 61.0 | | | 61.0 | | | | ��� | |
| 61.2 | | | | | | | ��� | |
| 61.4 | | | | | | | ��� | |
| 62.2 | | | | | | | ��� | |
| 62.4 | | | | | | | ��� | |
| 62.9 | | | | | | 62.9 | ��� | |
| 64.3 | | | | | | | ��� | |
| 64.9 | | | | | | | ��� | |
| 65.0 | | | | | | | ��� | |
| ��� | ��� | ��� | ��� | ��� | ��� | ��� | ��� | ��� |
| 65.4 | | | | | | | ��� | |
�@�s��\6.2�̂悤�ɃO���[�v��������ɂ́C�s���x���i�\6.4�ŗ��F�̔w�i�F�Ŏ������ӏ��j���E�N���b�N���āC�O���[�v�����擪�̒l60�C�����̒l90�C�P�ʁm��Ԃ̕��̂��Ɓn5���n�j�Ƃ���D
�@���ɁC���\6.2�̂悤�ɃO���[�v��������ɂ́C�x���i�\6.4�Ő��F�̔w�i�F�Ŏ������ӏ��j���E�N���b�N���āC�O���[�v�����擪�̒l60�C�����̒l90�C�P�ʁm��Ԃ̕��̂��Ɓn5���n�j�Ƃ���D
|
(2)�@���̗�̂悤�ɁC�ʓI�ϐ��|�ʓI�ϐ��̑g���s�{�b�g�e�[�u���ŏW�v����ƁC�\6.4�̍���[�i���F�̔w�i�F�Ŏ����Ă���j�̕\�����C�����ݒ�Łu���v�^����v�ƂȂ��Ă��āC�\�̒��̒l��61.0, 62.9, ...�ȂǂƏ����l�ɂȂ�D
�@�����ōs���Ă���N���X�W�v�̖ړI���猾���C�l�̍��v�͕s�v�Łu�f�[�^�̌��v�����߂����̂�����C����[�́u���v�^����v�ƂȂ��Ă��闓���E�N���b�N���f�[�^�̏W�v���@���f�[�^�̌���I�ԁD
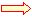
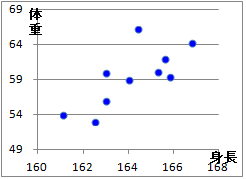
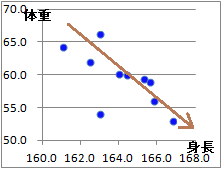
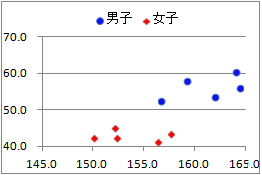
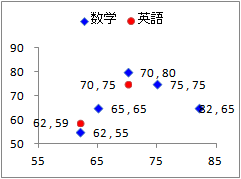
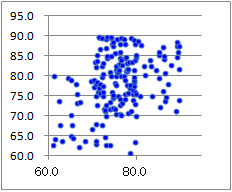
(3)�@���̃N���X�W�v�\�̏d�v�Ȃ˂炢�́C�}6.1�̎U�z�}�ł͕�����ɂ������Ƃ𐔒l�I�ɂ͂����肳���邱�Ƃ�����C�}6.1�Ɠ����`�ōs���x���iX�̊K�������j���~���ɂ��������悢�D���̂��߂ɂ́Cx�̗��i���F�̗��̓��̏�[�̂��́j���N���b�N���~����I�ԂƂ悢�D
(4)�@�\6.2�̍s���x���C�x��������ƁC�Ⴆ��60−65, 65−70 �̂悤�ɋ�Ԃ̋��ڂƂȂ��Ă���l�́C�����ɓo�ꂵ�܂��D���̂Ƃ��CExcel�̕��̓c�[�����q�X�g�O�������g�����ꍇ�̂悤�ȁC���̃\�t�g�Ɠ��́i�A�����J�����Ɠ��́H�j�Ȃ̂����������ɂȂ��Ă��Ȃ����ǂ����C��x�͒��ׂĂ��������悢�D
�@��̓I�ɂ́C�X�|�[�c�̏o�ꎑ�i�Łu�A���_�[18�v�Ƃ����悤�ȁ@X��18 �����R�ȕ������Ƃ��Ă��镶���ł́C60−65, 65−70�̈Ӗ���60<X��65, 65<X��70 �Ƃ��Ă���\��������̂ŁC���ڂƂȂ�lX=65.000���ǂ���ɕ��ނ���Ă��邩�ׂĂ����ق����悢�D�i�R�E�����R�c�̂悤�ɗ����ɓ���Ƃ������Ƃ͂��蓾�Ȃ��̂ŁC60<X��65�^��60��X<65�^��������D���{���������̃��|�[�g�ł́C60��X<65�^�����R�ȕ������ł��傤�j
�@�M�҂̊ȒP�ȃe�X�g�ł́C60��X<65�^�i�ȏ㖢���^�j�ɂȂ��Ă���̂ŁC���̂܂g���悢�悤�ł��D
|