← PC用は別頁

《統計的帰無仮説検定の問題点
　ｔ検定におけるサンプルサイズ設計を中心に
･･･用語と論点整理･･･表・図・例》

このページの主な内容･･･【目次】 以下は，統計の基本の復習･･･【忘れがちな論点のメモ】

統計的帰無仮説検定の問題点
　この項で(*1)などは，下記の論文の一部引用とする．

有意差検定

　我が国の学術論文に掲載されている研究の統計的仮説検定は，検定統計量の値と自由度，危険率や棄却率のみを報告している場合がほとんどであり，効果量の記載，検定力の分析はこれまで軽視されてきた．
…(*2)

ｐ値

　心理学の分野では，従来はネイマン・ピアソンの立場から5％水準を基準としてきたが，現代では5%水準を使いつつ，フィッシャーに近い立場が取り入れられている．APAでは，論文に記述するｐ値を正確に記入するように勧めている．すなわち，p<.05といった書き方ではなく，p=.023と行った書き方が推奨される．これは，ｐ値が小さいほど証拠として強いと認めようという立場の現れであると言える．現実的には，これまでにコンセンサスが得られている5%を基準としつつも，5%で2者択一的な解釈を行うのではなく，より柔軟にｐ値を解釈する流れになっている．
…(*8) 　

ｐハッキング（p−hacking）

　研究知見の再現性を低める要因は複数ありうる．その中でも，帰無仮説検定において有意水準に達した分析結果を人為的に得る問題ある研究実践，通称 p-hacking が問題視されている．
…(*5)
p hacking の具体例としては，（1）行った条件や測定した変数の一部しか報告しない，（2）参加者を少しずつ足しながら分析を行い，有意差に至ったところで止める，（3）様々な共変量を用いて分析を行い，有意になった組み合わせのみを報告する，といったものがある．
…(*5)

QRPs

　John, Loewenstein, & Prelec （2012）は，これら統計的妥当性が疑われる研究手法に「問題のある研究実践（Questionable Research Practices，あるいはQRPs）」という名前を与え，さらにアメリカ主要大学の心理学者約 5,000 名（うち回答者は 2,000名）を対象とした調査を行った．結果，回答者の半数以上の心理学者が QRPs を行っており，また彼らの多くがそうした行為を特に問題だとは考えていないことが浮かび上がってきた．
…(*5)

再現可能性危機

　プライミング効果とは，先行する刺激（プライマー）の処理が後の刺激（ターゲット）の処理を促進または抑制する効果のことを指す．（*脳科学辞典）
　社会心理学，特に社会的認知領域における研究知見の再現性が問題となっている．たとえば，Bargh, Chen, and Burrows（1996）の高齢者プライミングを用いた知覚－行動リンク研究は社会心理学におけるプライミング効果研究 で重要な地位を占めるが，追試に失敗しており再現性に疑義がもたれている．
…(*5)

APA（アメリカ心理学会）, ASA（アメリカ統計学会）の動き

　APA 論文作成マニュアルにおいて効果量を追記する必要があることが明記されて以降は，日本においても効果量の報告に対する重要性が多くの研究で指摘されるようになった．特に ASAが2016年に出した声明では，p 値の科学的有用性は認めつつも，p 値が有意水準を超えたかどうかのみによって科学的結論を行うことを厳しく批判している．
…(*3)

日本の心理学会の動き

　このような APA の方針に呼応して，国内においても「心理学における統計改革」が始まった．第 6 版の日本語訳が 2011 年に出版され，発達心理学会の「論文原稿 作成のための手引き」（2013 年 7 月改訂版），日本心理学会の「執筆・投稿の手びき」（2015 年改訂版）などが APA に準拠する方向で改訂され，論文誌に掲載される論文や学会でのポスター発表などで，有意性検定の結果とあわせて効果量や信頼区間が報告されるようになった．
…(*1)

サンプルサイズ

　標本効果量と標本の大きさの関係について分析した結果,研究者は検定力を明確に意識こそしていないが,効果量の小さいものに対しては標本を大きくして検定力を高めていることが示唆された。
…(*4)
p 値はサンプルサイズに依存する．一般に，サンプルサイズが増えるほど有意になりやすい．例えば，相関係数 r =.10 という小さな効果でも，サンプルサイズが 400 を超えると.05 水準で有意となる．このような有意水準とサンプルサイズの関係は，相関係数だけでなく，t 検定でも分散分析でもχ2検定でも同じように存在する．
…(*7)

サンプルサイズ設計

　あらかじめ「母集団で想定される差」を決めておき，その差を検出するのに適切なサンプルサイズを決定しようという発想がある．これが，検定力分析に基づくサンプルサイズ設計である．
…(*8) 　
（引用元の論文）
(*1)「心理学研究における統計改革の進展状況について」（土居淳子）
(*2)「"心理学研究"における効果量・検定力・必要標本数の展望的事例分析」（鈴川由美 他）
(*3)「教育工学における帰無仮説有意性検定と効果量」（城戸楓 他）
(*4)「教育心理学研究における統計的検定の検定力」（杉澤武俊）
(*5)「心理学における再現可能性危機：問題の構造と解決策」（池田功毅 他）
(*6)「社会心理学における"p-hacking"の実践例」（藤島喜嗣 他）
(*7)「『コンピュータ＆エデュケーション』と帰無仮説検定：統計手法の改革は進んでいるか？」（大久保街亜）
(*8)「「統計的有意」で満足していませんか？ｰ統計的帰無仮説検定の問題と対応ｰ」（奥田英昭）

アメリカ統計学会2016年の声明（要約）

背景

　多くの科学分野でp値（特に p < 0.05）を「発見の有無」の機械的判断基準として使う慣習が広まり，誤解・誤用が科学的信頼性を損なうことが問題視されていた．

結論

　アメリカ統計協会（American Statistical Association, ASA）の2016年の声明は，t検定や他の統計的検定におけるp値の限界と正しい使い方を明確に示しました．t検定を使う際には：
  • p値を唯一の判断材料としない
  • 効果量や信頼区間，検出力などの情報を併用
  • 研究目的・文脈に応じた解釈を行う
ことが推奨される．
アメリカ心理学会 出版マニュアルの第7版（2020年）
　アメリカ心理学会（APA: American Psychological Association）は，心理学研究における推測統計（仮説検定）の使用についていくつかのガイドラインを示しています．とくに「APA Publication Manual（出版マニュアル）」の第7版（2020年）は，t検定などを含む推測統計の報告と解釈に関する実務的な指針を明確に述べています．
① APAは，p値の報告を義務づけています
② 効果量（effect size）の報告は必須
③ 信頼区間（confidence intervals, CIs）の併記を推奨
④ 検出力（power）分析の実施と報告
事前に検出力分析を行い，適切なサンプルサイズを設計することが望ましいとされています（とくに実験研究）．
⑤⑥⑦以下略

第I種の過誤，第Ⅱ種の過誤，検出力
〇 第I種の過誤（type I error，あわて者の過誤）は，有意水準α（通常は0.05）で表され，「帰無仮説（H0）が成り立つときに，誤ってこれを棄却してしまう」ことをいう．･･･αは危険率とも呼ばれる．
〇 第Ⅱ種の過誤（type Ⅱ error，うっかり者の過誤）は，βで表され，「帰無仮説（H0）が成り立たないときに，誤って帰無仮説を採択してしまう」ことをいう･･･1−βは検出力（検定力）と呼ばれる．
〇　検定における2種類の誤り
検定における判断
H0を採択H0を棄却
前提H0が真
取り出した標本は同じ母集団のものだった		判断は正しい
1−α
同じ母集団の標本だと判断した		第I種の過誤
有意水準α
異なる集団の標本だと判断した
H0が偽
取り出した標本は異なる集団のものだった		 第Ⅱ種の過誤
β
同じ母集団の標本だと判断した		判断は正しい
検出力（検定力）1−β
異なる集団の標本だと判断した
〇　有意水準（α）と検出力1−βの関係
　有意水準（α）を厳しくすると，すなわちαを小さくすると，第Ⅱ種の過誤βが大きくなり，検出力1−βは小さくなる．逆に，有意水準（α）を緩くすると，すなわちαを大きくすると，第Ⅱ種の過誤βが小さくなり，検出力1−βは大きくなる．
　そこで，有意水準（α）を固定したときに，検出力1−βが最大となるような検定が望ましい．
〇　サンプルサイズ（N）が大きくなると，標本平均のばらつき（標準誤差SE）は小さくなる．
標準誤差（standard error of the mean）は以下の式で表されます
\( \displaystyle SE=\frac{\sigma}{\sqrt{N}}\)
　そこで，統計的な検定を行うときにサンプルサイズ（N）を大きくすると，実験群と対照群の重なりが少なくなって，2群が分離して行くので，どのような荒唐無稽な対立仮設でも証明できてしまうことが大きな問題になる．

検出力，効果量の目安
効果量の指標と大きさの目安（Cohen, 1988）
検定 効果量の指標 効果量
小中大
平均の差のｔ検定d0.200.500.80
相関r0.100.300.50
χ2検定ω0.100.300.50
分散分析f0.100.250.40
η20.010.060.14
回帰分析R20.020.130.26
f20.020.150.35
　効果量dは，研究分野や具体的な文脈によってその「大きさ」の解釈が異なります．Cohenの目安は一般的なガイドラインですが，常にそれに従う必要はありません．先行研究やパイロットスタディに基づいて適切な効果量を見積もることが重要です．
検出力の目安（一般的な基準）
検出力（Power） 評価 説明
0.70（70%）未満 不十分効果があっても検出できない可能性が高く，検定の信頼性が低い
0.80（80%） 標準的最も一般的に推奨される基準．β = 0.20（20%の見逃し許容）
0.90（90%） 望ましいより厳密な研究や医療などの分野では用いられることがある
0.95（90%）以上 非常に厳密臨床試験などで重要な効果の見逃しを極力避けたい場合に設定

検出力か，検定力か･･どちらの用語が適切か
　次の表は，英語で power（statistical powerまたは power of the test）を検出力・検定力のどちらの用語に訳すかを手元の資料で調べた結果です．これによれば，日本語の心理学関連論文では「検定力」が多いが，生成ＡＩでは「検出力」が推奨されています．
　なお，基本書Cでは，索引において検出力→検定力という形で，一方は他方の同義語として，本文では検定力に揃えられています．
　このページでは，折衷的に検出力（検定力）とする．
検出力検定力
基本書A, DB, C
論文(1), (2), (3), (4), (5), (6), (7), (8)
生成AI [a], [b], [c]
A「やさしい統計学」（現代教学社，田畑吉雄著）
B「心理統計法入門」（北大路書房，松田文子 他著）
C「心理統計学の基礎」（有斐閣アルマ，南風原朝和著）
D「医療統計学」（医療検査 Vol.74，佐藤正一 他著）

(1)「心理学研究における統計改革の進展状況について」（土居淳子）
(2)「"心理学研究"における効果量・検定力・必要標本数の展望的事例分析」（鈴川由美 他）
(3)「教育工学における帰無仮説有意性検定と効果量」（城戸楓 他）
(4)「教育心理学研究における統計的検定の検定力」（杉澤武俊）
(5)「心理学における再現可能性危機：問題の構造と解決策」（池田功毅 他）
(6)「社会心理学における"p-hacking"の実践例」（藤島喜嗣 他）
(7)「『コンピュータ＆エデュケーション』と帰無仮説検定：統計手法の改革は進んでいるか？」（大久保街亜）
(8)「「統計的有意」で満足していませんか？ｰ統計的帰無仮説検定の問題と対応ｰ」（奥田英昭）

[a] ChatGTP
検定力という言葉も日本語では時に見かけますが，一般には「検出力」の別表現として使われるだけで，正式な用語では「検出力」が推奨されます．「検定力」という用語はあいまいなので，学術的には避けるべきです．
[b] Google Gemini
日本語では「検定力」という言葉も使われますが，一般的には検出力がより広く用いられる用語です．
[c] Microsoft Copilot
「検出力」と呼ぶのが適切です！

◎ｔ検定における検出力設計
〇　t検定における検出力（statistical power）設計とは，「効果が本当に存在するときに，それを有意に検出できる確率」を事前に計画し，必要なサンプルサイズなどを決めるプロセスです．これはネイマン＝ピアソンの枠組みに基づく重要な考え方です．
〇　検出力の設計に必要な要素（4つ）
⇒　このうち 3つを決めれば，残り1つを計算できる．
要素 説明
① サンプルサイズ（n） 必要な参加者数（両群合計または片群あたり）
② 群間の平均差または効果量（effect size d） 群間の平均差deltaまたはそれを標準偏差で割った値（Cohen's d）
③ 有意水準（α） 通常は α=0.05（第I種の過誤）
④ 検出力（power） 通常は 1−β=0.8 または 0.9
（β= 0.2 または 0.1）
※効果量dは，群間の平均値の差\(delta=M_1-M_2\)を2群のプールされた標準偏差\(\displaystyle s_{pooled}=\sqrt{\frac{(n_1-1)s_1^2+(n_2-1)s_2^2}{n_1+n_2-2}}\)で割ったもの
\(\displaystyle d=\frac{M_1-M2}{s_{pooled}}\)

サンプルサイズなどの計算
〇 統計用フリーソフトRを用いて「サンプルサイズn」を求める計算は，power.t.test関数またはpwr.t.test関数を用いて行うことができる．これらの関数を使うとき，引数の指定方法が微妙に異なるので注意を要する．
〇 power.t.test関数はビルドイン（組込）関数なので，特別なインストール手順を経なくてもそのまま使えるが，pwr.t.test関数を使うには， 
install.packages("pwr")
library(pwr)
と書く必要がある．
〇 power.t.testでは，5つの主要なパラメータのうち，1つをNULL（または指定しない）にすることで，残りのパラメータからそのNULLの値を計算するようになっている．
　ただし，sdとsig.levelはデフォルトで（省略された場合）NULLではなく，それぞれ，1と0.05なので，これらを未知数として求めたいときは，明示的にsd=NULL, sig.level=NULLと書かなければならない．
　pwr.t.testでは，4つの主要なパラメータのうち，1つをNULL（または指定しない）にすることで，残りのパラメータからそのNULLの値を計算するようになっている．（pwr.t.testではsdは使わない）
power.t.testpwr.t.test
① n: サンプルサイズ（各群の標本数）
② delta:
絶対的な平均差μ1−μ2
（正の値のみ指定できる） 		② d:効果量 (Cohen's d)
②' sd:標準偏差
省略すれば1になる
③ sig.level: 有意水準 (α)　省略すれば0.5になる
④ power: 検出力 (1−β)
※効果量d
(1) 2群のサンプルサイズが等しく，標準偏差も共通SDのとき，効果量dは，次の式で表される．
\(\displaystyle d=\frac{M_1-M_2}{SD}\)
すなわち，平均差が同じでも標準偏差が小さいほど効果量は大きくなります．
(2) 2群のサンプルサイズや，標準偏差が異なるときは，効果量dは，次の式で表される．
群間の平均値の差\(delta=M_1-M_2\)を2群のプールされた標準偏差\(\displaystyle s_{pooled}=\sqrt{\frac{(n_1-1)s_1^2+(n_2-1)s_2^2}{n_1+n_2-2}}\)で割ったもの
\(\displaystyle d=\frac{M_1-M_2}{s_{pooled}}\)
〇他の引数
power.t.testpwr.t.test
⑤ type:検定の種類
"two.sample"(独立2群),
"one.sample"(1群平均)･･･あるグループのデータが特定の基準値と異なるかどうかを判断
"paired"(対応のあるt検定)
省略すれば"two.sample"になる
⑥ alternative:
"two.sided"(両側)，
"one.sided"(片側)
省略すれば"two.sided"になる
alternative:
"two.sided"(両側),
"less"(片側：小さい方),
"greater"(片側：大きい方)
省略すれば"two.sided"になる
⑦ strict:厳密な解釈
　両側検定において，真の効果とは反対方向の棄却確率が検出力に含まれる．デフォルトではstrict=FALSEなので，真の差がゼロの場合，検出力は有意水準の半分になる．RのHELPでは，「両側検定のときstrict=TRUEとする」とされているが，デフォルトのまま何も指定しなくても影響がないことが多い．

例(1) power.t.testを用いてサンプルサイズを求める
Rのプロンプトで次のように入力する
power.t.test(power = .90, delta = 1, alternative = "one.sided")
必須の引数
① サンプルサイズn：書かれていない⇒デフォルトでn=NULLとみなされ，サンプルサイズnを求める計算が行われる．
② 平均差：delta=1
標準偏差 sd：書かれていない⇒デフォルトでsd=1となる
③ 有意水準(α)：sig.level 書かれていない⇒デフォルトでsig.level=0.05となる
④ 検出力(1−β)：power=0.9
他の引数
⑤ 検定の種類 type：書かれていない⇒デフォルトでtype="two.sample"となる
⑥ 片側か両側か alternative = "one.sided"
実行結果: 
     Two-sample t test power calculation 

              n = 17.84713
          delta = 1
             sd = 1
      sig.level = 0.05
          power = 0.9
    alternative = one.sided

NOTE: n is number in *each* group
以上の計算により，実験群18件，統制群18件の合計36件のサンプルサイズが必要であることがわかります．

例(2) pwr.t.testを用いてサンプルサイズを求める
pwr.t.test関数を使うには，あらかじめ install.packages("pwr"), library(pwr) と書いておく必要がある．
Rのプロンプトで次のように入力する
pwr.t.test(d = 0.6, power = 0.8)
必須の引数
① サンプルサイズn：書かれていない⇒デフォルトでn=NULLとみなされ，サンプルサイズnを求める計算が行われる．
② 効果量：d=0.6
③ 有意水準(α)：sig.level 書かれていない⇒デフォルトでsig.level=0.05となる
④ 検出力(1−β)：power=0.8
他の引数
⑤ 検定の種類 type：書かれていない⇒デフォルトでtype="two.sample"となる
⑥ 片側か両側か alternative：書かれていない⇒デフォルトでalternative = "two.sided"となる
実行結果: 
     Two-sample t test power calculation 

              n = 44.58577
              d = 0.6
      sig.level = 0.05
          power = 0.8
    alternative = two.sided

NOTE: n is number in *each* group
以上の計算により，実験群45件，統制群45件の合計90件のサンプルサイズが必要であることがわかります．
　なお，pwr.t.test関数がうまくインストールできない場合は，power.t.test関数を用いて，効果量 d→平均差 delta，標準偏差 sd=1とすれば，同じ結果を得ることができる．
pwr.t.test(power = .80, d = 0.6, sig.level=0.5)の代わりに
power.t.test(power = .80, delta = 0.6, sd= 1, sig.level=0.5)を使う

例(3) power.t.testを用いて検出力を求める
Rのプロンプトで次のように入力する
power.t.test(n=20, delta=5, sd=10)
必須の引数
① サンプルサイズ n=20
② 平均差：delta=5
②' 標準偏差 sd=10
③ 有意水準(α)：sig.level 書かれていない⇒デフォルトでsig.level=0.05となる
④ 検出力(power)：書かれていない⇒デフォルトでpower=NULLとみなされ，検出力powerを求める計算が行われる．
他の引数
⑤ 検定の種類 type：書かれていない⇒デフォルトでtype="two.sample"となる
⑥ 片側か両側か alternative：書かれていない⇒デフォルトでalternative = "two.sided"
実行結果: 
     Two-sample t test power calculation 

              n = 20
          delta = 5
             sd = 10
      sig.level = 0.05
          power = 0.3377084
    alternative = two.sided

NOTE: n is number in *each* group
以上の計算により，検出力はpower≒0.338<0.7となり，この検定の信頼性は低い．（他の条件が同じで，サンプルサイズが80ならば検出力はpower≒0.88などとよい値になります）

例(4) pwr.t.testを用いて検出力を求める
Rのプロンプトで次のように入力する
pwr.t.test(n=30, d=0.7)
必須の引数
① サンプルサイズ n=30
② 効果量：d=0.7
③ 有意水準(α)：sig.level 書かれていない⇒デフォルトでsig.level=0.05となる
④ 検出力(power=1−β)：書かれていない⇒デフォルトでpower=NULLとみなされ，検出力powerを求める計算が行われる．
他の引数
⑤ 検定の種類 type：書かれていない⇒デフォルトでtype="two.sample"となる
⑥ 片側か両側か alternative：書かれていない⇒デフォルトでalternative = "two.sided"
実行結果: 
     Two-sample t test power calculation 

              n = 30
              d = 0.7
      sig.level = 0.05
          power = 0.7599049
    alternative = two.sided

NOTE: n is number in *each* group
以上の計算により，検出力はpower≒0.76となり，検出力がやや足りない

簡単なサンプルサイズの設計（練習問題）
〇　効果量\(\displaystyle d=\frac{delta}{sd}\)，有意水準(sig.level)，検出力（power）が与えられれば，望ましいサンプルサイズは決まる．そこで，最もよく使われる有意水準をsig.level=0.05とし，標準的な検出力をpower=0.8としたときの，効果量dとサンプルサイズnの対応表を求めておくと，次の表のようになる．
　（独立な2群のｔ検定で両側検定の場合，サンプルサイズは小数点以下を切り上げたもの）
効果量d0.50.60.70.80.91.01.11.2
サンプルサイズn6445342621171512
〇　具体的に，平均の差deltaと標準偏差sdが与えられた場合は，効果量\(\displaystyle d=\frac{delta}{sd}\)として，この表から望ましいサンプルサイズを求めることができる．
例1
delta=5, sd=10 ⇒ d=0.5 ⇒ n=64
例2
delta=12, sd=20 ⇒ d=0.6 ⇒ n=45
例3
delta=4, sd=5 ⇒ d=0.8 ⇒ n=26
※上の表にないdelta,sdの組については，Rのpower.t.testまたはpwr.t.testを用いて，計算するとよい．
例4
delta=6, sd=8 ⇒ d=0.75 ⇒ n=29
　power.t.test(power=0.8, sig.level=0.05, delta=6, sd=8) → n=29
　pwr.t.test(power=0.8, sig.level=0.05, d=6/8) → n=29
例5
delta=5, sd=4 ⇒ d=1.25 ⇒ n=12
　power.t.test(power=0.8, sig.level=0.05, delta=5, sd=4) → n=12
　pwr.t.test(power=0.8, sig.level=0.05, d=5/4) → n=12
〇　有意水準をsig.level=0.05とし，医療などの分野では用いられる検出力をpower=0.9としたときの，効果量dとサンプルサイズnの対応表を求めておくと，次の表のようになる．
　（独立な2群のｔ検定で両側検定の場合，サンプルサイズは小数点以下を切り上げたもの）
効果量d0.50.60.70.80.91.01.11.2
サンプルサイズn8660443427231916
例6
delta=4, sd=5 ⇒ d=0.8 ⇒ n=34
例7
delta=12, sd=10 ⇒ d=1.2 ⇒ n=16
例8
delta=3.5, sd=9 ⇒ d=3.5/9 ⇒ n=140
　power.t.test(power=0.9, sig.level=0.05, delta=3.5, sd=9) → n=140
　pwr.t.test(power=0.9, sig.level=0.05, d=3.5/9) → n=140
統計的帰無仮説検定（要約）
〇　統計を用いて，「ある実験群とその統制群の母平均が異なる」という命題（これを記号H1で表す）を証明したいとき，H1を直接的に証明することが難しいとき，その否定「ある実験群とその統制群の母平均が等しい」という命題（これを記号H0で表す）を仮定して，矛盾が生じることを示すことにより，H1が成立することを証明する．（数学で背理法と呼ばれる証明方法を用いる）
　矛盾の内容として，観察された事柄が起こる確率が非常に小さい（確率5%以下がよく使われる）ということを用いる．
　ここで，H0を帰無仮説，H1を対立仮設と呼ぶ．すなわち，証明したい方を対立仮設H1とし，その否定として証明したくない方を帰無仮説H0とし，H0を仮定したら，めったに起こらない確率になる場合に，帰無仮説を棄却して対立仮設を採択する．
〇　統計的帰無仮説検定の手順は，次の3段階にまとめることができる．
  • ① 証明したい命題を対立仮設H1とし，その否定として証明したくない命題を帰無仮説H0として仮定する
  • ② 帰無仮設が成り立つと仮定したとき，ある観察事実が起こる確率pが，あらかじめ設定された有意水準α（確率5%以下がよく使われる）よりも小さくなるかどうかを調べる
  • ③ p<αのとき，帰無仮説H0を棄却して，対立仮設H1を採択する．
    （p≧αのときは，帰無仮説H0の成立が示されたとは考えない．積極的に主張できる命題はなくなったと考える．）
（背理法の使い方の例）
数学での例A統計での例B
証明したい事\(\sqrt{2}\)は無理数である10円硬貨を4回投げて表が4回出たとき，この硬貨は正しく作られていない⇔これを対立仮設H1とする
①「\(\sqrt{2}\)は有理数である」と仮定する
\( \Downarrow \)
\(\displaystyle \sqrt{2}=\frac{p}{q}\)（\(p,q\)は整数で互いに素）とおく		表が出る確率と裏が出る確率は等しい\(\displaystyle (\frac{1}{2})\)と仮定する⇔これを帰無仮設H0とする
②※下記の計算参照
\(p,q\)とも2の倍数となって，数学的な矛盾が起こる		表が4回連続で出る確率は\((\frac{1}{2})^4=\frac{1}{16}=0.0625\)
統計的な矛盾(p<0.05)は起きていない
③「\(\sqrt{2}\)は無理数である」ことが言える\(p=0.0625\gt 0.025\)だから，帰無仮説は棄却できない
（この場合，背理法による証明はできていない）
※ ①から，\(\displaystyle \sqrt{2}q=p\)の辺々を2乗すると，\(\displaystyle 2q^2=p^2\)
2乗が2の倍数になるから\(p\)は2の倍数．
そこで\(\displaystyle p=2k\)（ \(k\)は整数）とおく
\(\displaystyle 2q^2=4k^2\)より\(\displaystyle q^2=2k^2\)
2乗が2の倍数になるから\(q\)も2の倍数．

質的データ，量的データと尺度，水準
尺度内容具体例
質的デ
|
タ		名義尺度順序がなく，ただ分類するためのラベル
（最頻値がある）		血液型（A・B・O・AB）,性別（男・女）,都道府県（北海道・東京都・大阪府）
順序尺度順序はあるが，差の大きさは意味を持たない
（最頻値，中央値がある）		満足度（満足・ふつう・不満），成績（優・良・可・不可），スポーツの順位（ 1位・2位・3位）
量的デ
|
タ		間隔尺度データの順序に意味があり，さらにデータ間の間隔（差）にも意味がある．しかし，絶対的なゼロ点が存在しない
（最頻値，中央値，平均値，標準偏差がある）		気温（℃や°F），西暦，テストの点数，IQ（知能指数）
比例尺度
(比率尺度)
（比尺度）		データの順序にも間隔（差）にも意味があり，さらに絶対的なゼロ点が存在する．そのため，比率にも意味がある．
（平均値，標準偏差，比率など，あらゆる統計分析が可能）		年齢，収入，身長，体重，時間
〇　尺度は，上記のように４種類に分けられる．
〇　水準（level）という用語は，それぞれ全く異なる文脈の中で使われる．
  1. 尺度のことを尺度水準ということがある．すなわち，データには名義尺度，順序尺度，間隔尺度，比例尺度の４つの水準があると考える
  2. 質的データの取りうる値のことを水準という．たとえば，血液型はA・B・O・ABの4水準からなる
    満足度調査では，非常に不満，不満，普通，満足，非常に満足の5水準で調査されることが多い
    量的データについても「温度を10°C,20°C,30°Cの3水準で実験を行う」という言い方をする
  3. 有意水準5%とか信頼水準95%のように，決まった術語として使われる

実験群と対照群
〇　ある処置に効果があるかどうかを統計を用いて調べたいとき，その処置を受ける群を「実験群」「処置群」といい，処置を受けずに比較に用いる群を「対照群」「統制群」などという．
以下は，生成ＡＩ:［Microsoft Copilot］に対して「統計における実験群と統制群の働きをまとめてください」と入力したときに返された答案（引用）

実験群と統制群の役割
項目 実験群（処置群）対照群（統制群）
定義 研究で何らかの介入や処置を受けるグループ 介入や処置を受けず，比較の基準となるグループ
目的 処置の効果を観察・測定するため 実験群との違いを明確にすることで，処置の真の効果を判断する
例 新薬を投与された患者 プラセボ（偽薬）を投与された患者
データの使い方 効果が現れたかどうかを見る 変化が自然発生か処置によるものか判断する
なぜ両方必要？
実験群だけだと「その変化が本当に処置のせいか」が分かりません．
対照群と比較することで，処置以外の要因（環境，時間，心理的効果など）を排除し，科学的に信頼できる結論を導くことができます．
〇　対照群が観測データとして与えられずに，平均，標準偏差が定数として与えられる場合 ⇒ １標本のZ検定と呼ばれる
【例】
　全国平均が50点，標準偏差が10点であることが分かっている小学校6年生の算数のテストで，ある小学校6年生40人の平均が53.5点であるとき，この小学校6年生の算数の得点は，全国平均と比べて有意な差があると言えるか
【解答】
　\(\displaystyle Z=\frac{53.5-50}{10/\sqrt{40}}=2.213\)
有意水準5%で両側検定の場合の限界値1.96と比較すると，Z>1.96だから，この小学校の算数の得点は，全国平均と比べて有意な差があると言える

両側検定にすべきか，片側検定にすべきか
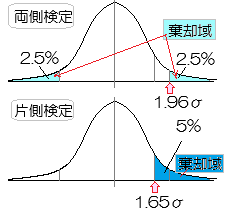
〇　両側検定，片側検定の違いは，統計的帰無仮説検定の手順の第2段階で，
「実験群の母集団平均M1と対照群の母集団平均M2は等しくない」
という事の意味を，どう捉えるかで変わる．
M1≠M2，すなわち，M1<M2でもM1>M2でもよいと解釈するのが両側検定
〇　これに対して，上記の例Bにおいて，対立仮設H1を「表が出る確率が，裏が出る確率よりも大きい」として，帰無仮説H0を「表が出る確率と裏が出る確率は等しい\(\displaystyle (\frac{1}{2})\)とする」場合は片側検定になる．
〇　棄却域を両側にとって，合計で5%とすると，片方の棄却域の確率は各々2.5%となり，中央から約1.96σだけ離れた値が限界値となる．
　これに対して，対立仮設としてM1<M2（またはM1>M2）だけを選ぶと片側検定となり，棄却域に入る確率は一方だけで5%となり，中央から約1.65σだけ離れた値が限界値となる．
　当然のことながら，片側検定にすると一方の棄却域が広がるので，対立仮設が成立し易くなるが，両側検定か片側検定かの判断において，データ収集後に「判断の楽な方を選ぶ」ようなことは厳に慎まなければなければならないとされている．
〇　データが集まれば，両側検定・片側検定が決まるのではない．データそれ自体には検定の向きはない．そのデータをもとに両側検定で判断するか，片側検定で判断するかは，分析者の関心が何にあるかによって決まる．しかし，それは分析者の気分次第でどちらでも選べるということではない．
〇　「実験群の平均が対照群の平均よりも大きくなる場合しか考えない．逆や等しい場合は意味がない」=生徒1人ずつのパソコンを整備するための予算を付けてもらうための資料として，パソコンを使って授業をしたら成績が下がる場合も含めた有意差（両側検定）があっても議員が納得しない．億単位の予算を付けてもらうには，パソコンを使って授業を行えば成績がよくなることを証明する必要がある．このような場合は片側検定でしょう．
　しかし，「片側検定にしなければならない特別な事情が説明できる場合を除けば，ほとんどの場合は両側検定で行う」と決めると分かりやすい．

仮説検定で対立仮設と帰無仮説を入れ替えることはできるか
〇　状況説明：帰無仮説をH0，対立仮設をH1として，統計的帰無仮説有意差検定を行ったところ，有意差が認められず研究をまとめることができなかった．この場合，対立仮設と帰無仮説を入れ替えて有意差検定を行うことはできるかというのが，素朴な疑問です．
〇　この疑問に対しては，Google Geminiの答案「対立仮説と帰無仮説を単純に入れ替えることはできない」というのが，端的に分かりやい．
　すなわち，他の生成AIでも，理論上は様々な難点が指摘されるが，「母集団の平均が等しくない」と仮定した場合に，等しくない場合は無限にあり，実際上の確率の計算ができない．
　これに対して，「母集団の平均が15異なる」などと具体的な差が仮定できれば，計算できる．

ネイマン・ピアソンとフィッシャー
仮説検定の解釈の違い
以下は，Microsoft Copilotによる要約

ネイマン・ピアソンの立場：意思決定の枠組み

（ネイマン・ピアソン理論のイェルジー・ピアソンは，積率相関係数の提唱者カール・ピアソンの子供）
  • 目的：事前に定めた誤りの確率（第一種・第二種）をもとに，最適な意思決定を行う．
  • 帰無仮説と対立仮説：両方を明確に定義し，検定力（1−β）を最大化するような検定を設計．
  • 有意水準（α）：第一種の誤り（誤って帰無仮説を棄却する確率）を事前に固定．
  • 検定結果：帰無仮説を「棄却する」か「棄却しない」かの二択．確率的な判断ではなく，ルールに基づく決定．
  • 特徴：頻度主義的で，長期的な誤り率の管理を重視．

フィッシャーの立場：証拠の評価

  • 目的：データから帰無仮説に対する「証拠の強さ」を評価する．
  • 帰無仮説のみ：対立仮説は明示せず，帰無仮説が正しいと仮定してP値を計算．
  • P値：観測されたデータ以上に極端な結果が得られる確率．小さいほど帰無仮説に対する証拠が強い．
  • 有意水準（α）：参考値として使われることが多く，厳密な意思決定ルールではない．
  • 検定結果：帰無仮説を「棄却するかどうか」ではなく，「どれだけ疑わしいか」を判断．
  • 特徴：探索的で，柔軟な解釈を許容．

主な違いまとめ

観点 ネイマン・ピアソン フィッシャー
仮説の扱い H0とH1を明示 H0のみ
有意水準 固定して意思決定 参考値として使用
P値の意味 使用しない／補助的 証拠の強さを示す
検定の目的 誤り率を管理して意思決定 帰無仮説の妥当性評価
哲学 頻度主義・決定理論 探索的・柔軟な解釈
〇 ネイマン・ピアソンとフィッシャーの解釈の違いは，統計学の歴史において重要な論争点でしたが，実際的な研究現場では，しばしば折衷主義的なアプローチが採用されています．これは，両者の考え方の要素を組み合わせ，それぞれの利点を生かそうとする試みと言えます．

リッカート尺度（Likert Scale）とは
以下は，以下は，生成ＡＩ:［ChatGTP］［Google Gemini］［Microsoft Copilot］からから得られた答案の引用です
〇　リッカート尺度（Likert scale）は，アンケート調査でよく使われる 心理測定法 の一つで，回答者の意見や感情の度合いを 数値化 して測定するための方法です．1932年にアメリカの社会心理学者レンシス・リッカート（Rensis Likert）によって考案された．
〇　例1：授業満足度に関する質問
質問：この授業はわかりやすかったですか？
回答選択肢（5件法）：
  1. 全くそう思わない
  2. あまりそう思わない
  3. どちらとも言えない
  4. ややそう思う
  5. とてもそう思う
〇　例2：働きがいに関する調査（職場環境）
質問：職場で自分の意見が尊重されていると感じますか？
回答選択肢（4件法）：
  1. まったくそう思わない
  2. あまりそう思わない
  3. ややそう思う
  4. 非常にそう思う
※ 選択肢が奇数個の場合は，簡単にして3択にする場合や，もっと詳しく7択，9択にすることもあるが，5択が多い．
※ 上記の例1のように「どちらとも言えない」という選択肢は「中立的な選択肢」と呼ばれる．
　これに対して，上記の例2のように「どちらとも言えない」という選択肢を含めない偶数個の選択肢からなるものは，分析者の都合で「どちらか一方を選んでほしい」ときに用いられる．
　このような偶数個の選択肢からなるものは， 偶数個のリッカート尺度は
  • 中立を排除することで意思決定を促す効果があるが，
  • 回答者の本当の意図が「中立」や「無関心」である場合，その意図を正確に反映できず，回答傾向に人工的な偏り（確率的な偏在）が生まれる．賛否が誇張され，「意見が分かれている」「対立がある」と誤認するリスクがある．
※新聞社の内閣支持率アンケート調査は，統計の論文に使えるようなリッカート尺度とはかなり異なるもののようである（筆者の感想）
• Ｍ社「〇〇内閣を支持しますか」→一択で，質問の中には解答はない．「はい」「いいえ」で答える：支持率は低くなる傾向がある．
• Ａ社「〇〇内閣を支持しますか，支持しませんか」→二択になっている．
• Ｙ社「あなたは，〇〇内閣を，支持しますか，支持しませんか」で第1段の質問を行い，答えられなかった人に対して，第2段として「どちらかと言えば，支持しますか，支持しませんか」と聞く：Ｍ社よりはも支持率は高くなる傾向がある．
※昔から言われている噂話として，新聞社名を聞けばその会社の答えてほしそうな回答に合わせていく傾向があると言われている．

リッカート尺度における中立的選択肢の役割
主に以下の点が挙げられます．
(1) 回答者の負担軽減と正直な回答の促進:
特定の意見を強く持っていない，あるいはどちらとも言えないと感じる回答者にとって，中立的選択肢は正直な回答を可能にします．もし中立的選択肢がなければ，回答者は無理にどちらかの意見に寄せるか，無回答を選ぶことになりかねません． 意見がないにもかかわらず，回答を強制されるストレスを軽減し，回答の質を高めることに繋がります．
(2) データの正確性の向上:
中立的選択肢を設けることで，意見が明確ではない回答者を適切に分類できます．これにより，データの分布がより正確に反映され，偏りのある結論を導くリスクを減らすことができます． 強制的にどちらかの極に振り分けられた回答は，本来の意見を反映していないため，分析の精度を低下させる可能性があります．
(3) 態度の中立性の把握:
単に意見がないだけでなく，本当に中立的な態度や，その問題に対して関心がない状態を示す回答者を区別できます．これは，特定のトピックに対する人々の態度をより深く理解するために重要です．
(4) 回答スキップの防止:
明確な意見がないために，質問をスキップしてしまう回答者を減らす効果も期待できます．中立的選択肢があることで，少なくとも何らかの回答を促すことができます．
中立的選択肢を設けることの潜在的なデメリット（考慮すべき点）:
(1) 「とりあえず」の中立回答の増加:
意見がない，あるいは考えるのが面倒だと感じる回答者が，安易に中立的選択肢を選んでしまう可能性があります．これにより，データに深みがない，あるいは情報が少ない状態になることがあります．
(2) 分析の複雑化:
　中立的選択肢の回答をどのように扱うか（例えば，中央値や平均値の算出において）について，検討が必要になります．
※回答に困るような難しい質問やセンシティブな内容が含まれる場合に，「全くそう思わない/あまりそう思わない/どちらとも言えない/ややそう思う/とてもそう思う」からなる選択肢に「わからない」という選択肢も追加するような場合は，慎重な取り扱いが必要になる．「わからない」は「どちらとも言えない」と同じではなく，回答拒否，あるいは白紙答案のようなもので，別枠に集計すべきものとなる．

ｔ検定におけるリッカート尺度の頑健性
　そもそもリッカート尺度は，質的データの順序尺度になっており，選択肢が心理的な等間隔に並んでいるという保証はなく，平均値や分散といった計算が，理論上はｔ検定が使える前提を満たしていない．
　またこのようなアンケート結果（人間の気分の分布）は正規分布にはならないと考える学者もいる．
\( {\Big \Downarrow}\)

リッカート尺度で集計したデータにt検定を使っていいか？

\( {\Big \Downarrow}\)

理論的には：

  • t検定は本来 量的データ（間隔尺度以上） を前提としている．
  • リッカート尺度は 順序尺度なので，厳密にはt検定の前提を満たさないとされる．

しかし，実務上は：

  • リッカート尺度の項目が複数あり，それらを平均化したスコア（例：質問5項目の平均点）を用いると， 近似的に 連続変数（間隔尺度的）として扱えることが多く，
  • t検定を使っても結果が大きく歪むことは少ない＝ある程度の頑健性がある．

リッカート尺度におけるt検定の頑健性まとめ

条件 t検定の頑健性 理由・注意点
複数項目の平均（尺度得点） 頑健性あり 中心極限定理により，近似的に正規分布とみなせるため，t検定の前提を概ね満たす．
サンプルサイズが大きい場合 頑健性高まる 中心極限定理により，データの分布が正規に近づくため．
分散が等しくない場合 △ Welchのt検定を使えば頑健性が増す
〇　リッカート尺度に対するt検定は，理論的には量的データの前提を満たしていないものの，実務上は頑健性が高いため広く使われている．ただし，サンプルサイズや分布の形状に注意を払い，必要に応じて代替手法を検討することが重要．

...メニューに戻る