|
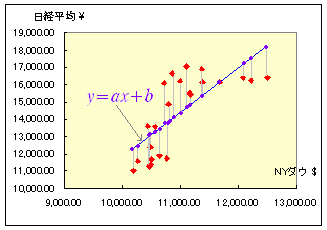
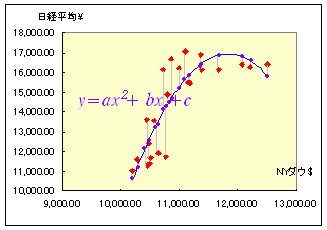
■解説 (1) 一番簡単な最小二乗法 右の表は,2005.1月〜2006.12月までの月ごと(5日頃)のNYダウ平均株価(単位ドル)と日経平均株価(単位円)です. [資料の出所:http://finance.yahoo.com/ のデータベース] これらを散布図に表わすと下のグラフのようになります. 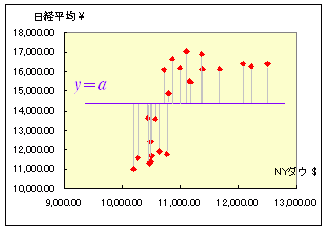 このとき,yの値(日経平均)を1つの定数 a で近似するには,図の青で示した横線(y=a)を求めることになります. 図の赤で示した測定値と青で示した予測値の差は,灰色の線の長さで示されますが,正負の符号があるので,単純にデータの個数分足せば消えてしまいますので,2乗を考え,(測定値-予測値)2の和: S=(y1-a)2+ (y2-a)2+ (y3-a)2+ ・・・+ (yn-a)2 ・・・(A) が最小となる a の値を求めることにします. この問題のように,(測定値-予測値)2の和が最小となるような予測値を求める方法は最小二乗法と呼ばれます. |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| [求め方] ■ソルバーを利用するための準備: 1) 定数a を書き込むセルを1つ用意します. セルA27に1と記入します.これは初期値(仮の値)で,後にソルバーによって,この値を増減させて条件に合うものを探すことになります.(ここに記入するのは,数値です.計算式ではありません.)なお,自分自身が分りやすいように,その上に「定数」などと書き込んでおきましょう. 2) セルD2に =(C2-$A$30)^2 と記入し,この式をコピーし,D3からD25に貼り付けます. D2に書かれた式は(A)の(y1-a)2に対応します. D3は(A)の(y2-a)2という式に対応します. ・・・(以下同様)・・・ ※ セルD2に記入するものは, =(C2-A27)^27 ではありません.もしそのように書き込むと,その式をコピーし,D3に貼り付けたとき =(C3-A28)^2 となって,引く側もずれます. 3) セルD27で,ショトカットアイコンのΣを押し,範囲をD2:D25とします.(=SUM(D2:D25)と直接書き込んでもよい.または,メニュー→「挿入」→「関数」→「数学/三角」→SUM→数値1をD2:D25とします.) ■これで準備ができたので,ソルバーを用いて最小二乗法により,「A27の値を変化させて,D27が最小となれば止まる」ようにします: 4) メニュー→「ツール」→「ソルバー」→ 目的セル:$D$27 目標値:最小値 変化させるセル:$A$27 オプション:反復回数1000,精度0.001,収束0.001,反復結果の表示にチェック・・・この程度から始めると収束しやすいようです.高い精度が必要なときは,一旦値を書き込んでから「精度」や「収束」を厳しく(0.0001などに)するとよいでしょう. 5) 「実行」ボタンを押す.(上の4)で反復結果の表示チェックを入れておくと,1回で目的の値にたどり着かないときに,「継続」ボタンを押して漸近していけます.) 何回か「継続」ボタンを押し,[最適解が見つかりました]と表示されたら,[解を記入する]の状態でOK 6) 結果の検討 ○ 上で求めたaの値は,14406.4 となります. ○ 裏付けで確かめる:(コンピュータで処理しても,入力ミス,転記ミス,操作ミスなどはつきものです.別の方法で確認できるときは確認する方がよい.右の参考に示すように,ここで求めたaの値はyの平均値となっており,=AVERAGE(C2:C25)の値と一致するはずです.) |
(参考) ここで求めたa の値は,次の変形で分るようにy の平均値となっています: S=(y1-a)2+ (y2-a)2+ (y3-a)2+ ・・・+ (yn-a)2が最小となるa の値を求める⇔2次関数Sが最小となるaの値を求める⇔頂点の座標aを求める 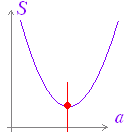 =na2 - 2a(y1+y2+···+yn)+... =n { a2 - 2a(y1+y2+···+yn) / n} + ... =n(a - (y1+y2+···+yn) / n}2+... の頂点の座標(軸)a は a = (y1+y2+···+yn) / n となり,a が y の平均値に等しいときに,S は最小となります. |