|
���̃y�[�W�ł́C�O���t�̕`������Excel���g���Đ������܂��D
1.�@�c�_�O���t�C���_�O���t
1.1�@�_�O���t
(1) ���ʂ̑召���r����̂ɓK���Ă���
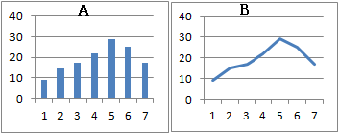
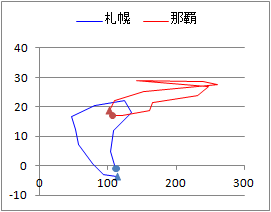
(2) �c�_�O���t�ł͖_�̍����C���_�O���t�ł͖_�̉��������ʂ�\�� 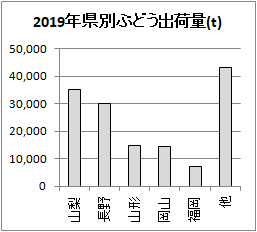 �y��1.1�z
�y��1.1�z�@�E�̃O���t�́C2019�N�s���{���ʂԂǂ��o�חʁi�P�ʂ��j--�_�ѐ��Y�Ȍ��\����--���c�_�O���t�ɂ������̂ł��D �@���̃f�[�^�́C�k�C������n�܂�s���{���ԍ����ɕ���ł��܂����C�O���t�ɂ���Ƃ��́C �@A) ���̓s���{�����C�@ B) ���ʂ̑������i���Ȃ����j ���l�����܂��D���̃O���t�ł�B�̐��ʂ̑������Ƃ��āC���5���܂łƑ��̍��v��\���������̂ł��D 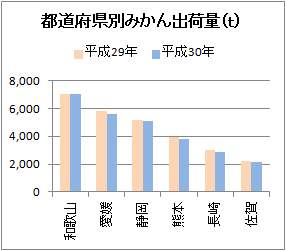 1.2�@�����n��̖_�O���t
1.2�@�����n��̖_�O���t�y��1.2�z �@�E�̃O���t�́C����29�N�ƕ���30�N�̓s���{���ʂ݂���o�חʁi�P�ʂ��j--�_�ѐ��Y�Ȍ��\����--���c�_�O���t�ɂ������̂ł��D �@���̃O���t�ł͏��6���܂ł�\���������̂ł��D �@���̃O���t�̂悤�ɁC���ꃉ�x���i�s���{���j�ɑΉ�����Q�̔N�̐��ʂ�_�O���t�ɂ������̂́C�����n��̖_�O���t�ƌĂ�܂��D
�@�}�����c�_��2D�c�_ �Ƃ���悢�D |
 1.3�@�����O���t
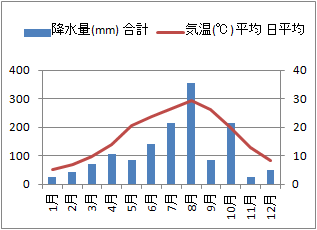
1.3�@�����O���t�y��1.3�z �@�E�̃O���t�́C2019�N���s�s�̌����̍~����(mm)�ƕ��ϋC��(��C)���P�̃O���t�ɂ܂Ƃ߂����̂ł��D �@���̂悤�ȕ����O���t�́C�C���ƍ~���ʂ̊W�H�Ƃ����悤�ȋ^��ɓ����邽�߂̂P�̎肪�����^����D �@MicroSoft Excel���g���āC���̃O���t��`���ɂ́C(A) ��2�Ɠ��l�ɕ����n��̖_�O���t���쐬���遨�C����\���c�_�O���t�̂P���E�N���b�N���n��O���t�̎�ނ̕ύX���܂���O���t�C�̎菇�ōs�����Ƃ��ł��܂��D(B) �����n��̐܂���O���t�ɂ��Ă����Ă���C�~���ʂ̃O���t��_�O���t�ɕύX���Ă����l�̌��ʂ������܂��D �@���̗�̂悤�ɁC�~���ʂ̒P��(m)�̖ڐ���������ɁC�C��(��C)�̖ڐ�����E���ɕ\������ɂ́C(AB�Ƃ�) �܂���ɂȂ����C���̃O���t���E�N���b�N���f�[�^�n��̏����ݒ聨�n��̃I�v�V���� ��2��(��/�E��)�C�̎菇�ōs�����Ƃ��ł��܂��D |

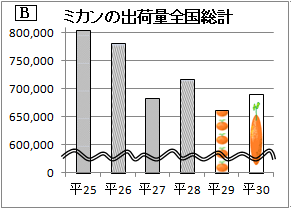 �@�@Excel�O���t�ŁC�O���tB�̂悤�ɂO�������ɂ�
�@�@Excel�O���t�ŁC�O���tB�̂悤�ɂO�������ɂ� �@Excel2007�ł��i���̃o�[�W�����ł��j�Z���̏����Ƃ��āu�E�オ��ΐ��v�u�E������ΐ��v�Ȃǂ́u�h��Ԃ��v�͂ł���D�����ŁC�E�}�̂悤�ȊG���R�s�[�\��t�����āC�y�C���g�ŕۑ����܂��D���̃t�@�C����ۑ������t�H���_���t�@�C�������o���Ă����āC���̍�Ƃ����܂��D
�@Excel2007�ł��i���̃o�[�W�����ł��j�Z���̏����Ƃ��āu�E�オ��ΐ��v�u�E������ΐ��v�Ȃǂ́u�h��Ԃ��v�͂ł���D�����ŁC�E�}�̂悤�ȊG���R�s�[�\��t�����āC�y�C���g�ŕۑ����܂��D���̃t�@�C����ۑ������t�H���_���t�@�C�������o���Ă����āC���̍�Ƃ����܂��D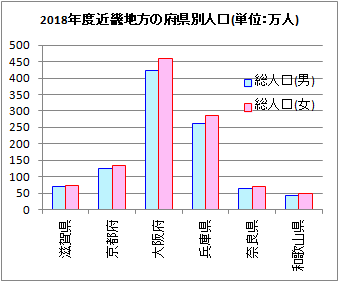

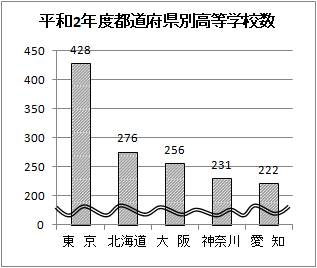
 �@Excel�ő}�����c�_�O���t��I�ԂƁC��U�C���̐}�̂悤�ɂȂ��āC�ł��Ăق������̂ƈႤ�`�̃O���t�ɂȂ�܂��D
�@Excel�ő}�����c�_�O���t��I�ԂƁC��U�C���̐}�̂悤�ɂȂ��āC�ł��Ăق������̂ƈႤ�`�̃O���t�ɂȂ�܂��D �@����ɂ��C���̂悤�ȃO���t�ɕς��܂��D
�@����ɂ��C���̂悤�ȃO���t�ɕς��܂��D
 �@�c�_�O���t�ɂ��邩���_�O���t�ɂ��邩�́C�r������ł��ύX�ł��܂��D
�@�c�_�O���t�ɂ��邩���_�O���t�ɂ��邩�́C�r������ł��ύX�ł��܂��D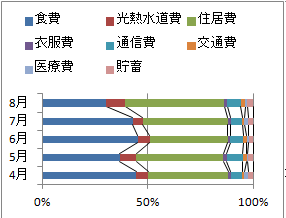 �@�ςݏグ�_�O���t�Œ����̑������`�ŁC�S�����\���ɂ������̂́C
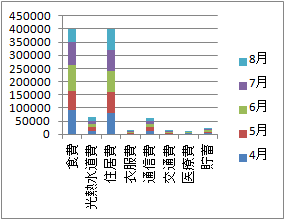
�@�ςݏグ�_�O���t�Œ����̑������`�ŁC�S�����\���ɂ������̂́C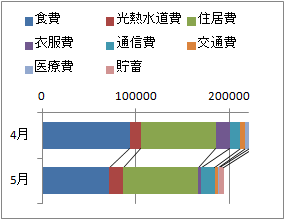 �@�E�̃O���t�́C����l�̍��N4���C5���̉ƌv�x�o�z�����������̂ł��D
�@�E�̃O���t�́C����l�̍��N4���C5���̉ƌv�x�o�z�����������̂ł��D

 �@���̗�ł́C(B)�̑уO���t�̕�����茩�₷���ł��傤�D
�@���̗�ł́C(B)�̑уO���t�̕�����茩�₷���ł��傤�D
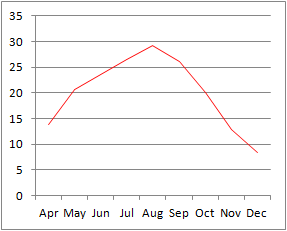
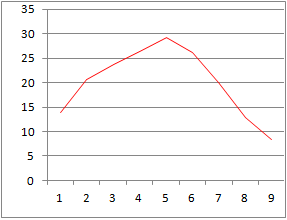 �@�܂���O���t��`���Ƃ��ɁC���x�̃f�[�^�����̂P�̗��I�������ꍇ�C�E�̂悤�ȃO���t�ɂȂ�܂��D���̂Ƃ������ɕt�����郉�x���͌����ł͂Ȃ��C���̃f�[�^�̔ԍ��ɂȂ�܂��̂ŁC�P�͂P����\���Ă��܂���D���̂悤�ɐ܂���O���t�����Ƃ��ɁC�����̃��x����z��ʂ�ɕt����ɂ́C�O���t�̃f�[�^�Ƃ��āC�����̃��x�����܂ޗ�f�[�^���܂߂Ďw�肷��Ƃ悢�D
�@�܂���O���t��`���Ƃ��ɁC���x�̃f�[�^�����̂P�̗��I�������ꍇ�C�E�̂悤�ȃO���t�ɂȂ�܂��D���̂Ƃ������ɕt�����郉�x���͌����ł͂Ȃ��C���̃f�[�^�̔ԍ��ɂȂ�܂��̂ŁC�P�͂P����\���Ă��܂���D���̂悤�ɐ܂���O���t�����Ƃ��ɁC�����̃��x����z��ʂ�ɕt����ɂ́C�O���t�̃f�[�^�Ƃ��āC�����̃��x�����܂ޗ�f�[�^���܂߂Ďw�肷��Ƃ悢�D



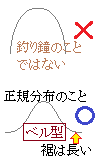 �x���^�Ƃ����̂́C���m�̋���̏��̌`�Ƃ������ƂŁC���{�ł悭����ނ���̌`�ł͂Ȃ��D�ǂ��炩�Ƃ����C�u�����X�q�̌`�v�u�}�C�t�F�A���f�B�̖X�q�v�u���̒����x�m�R�̌`�v�̂��Ƃ��x���^�ƌ������킵�Ă���D
�x���^�Ƃ����̂́C���m�̋���̏��̌`�Ƃ������ƂŁC���{�ł悭����ނ���̌`�ł͂Ȃ��D�ǂ��炩�Ƃ����C�u�����X�q�̌`�v�u�}�C�t�F�A���f�B�̖X�q�v�u���̒����x�m�R�̌`�v�̂��Ƃ��x���^�ƌ������킵�Ă���D �@���z������^�ɂȂ�ꍇ�́C���̏W�c�̒��ɑ�l�Ǝq���̂悤�Ɉَ��ȏW�c���������Ă���\��������D�������C���Z���w���̉p��␔�w�̂悤�ɁC�D���������͂����蕪����Ă��܂����Ȃ̓��_������^�ɂȂ邱�Ƃ�����D
�@���z������^�ɂȂ�ꍇ�́C���̏W�c�̒��ɑ�l�Ǝq���̂悤�Ɉَ��ȏW�c���������Ă���\��������D�������C���Z���w���̉p��␔�w�̂悤�ɁC�D���������͂����蕪����Ă��܂����Ȃ̓��_������^�ɂȂ邱�Ƃ�����D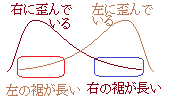

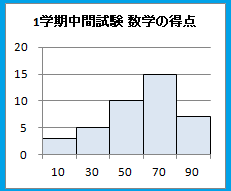
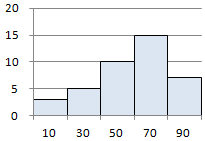 �@�E�̓x�����z�\�ɂ��āC�u�x���^�v�u�P��^�v�u����^�v�u���E�Ώ̌^�v�u�E�ɘc��ł���v�u���ɘc��ł���v�u��l�ȕ��z�v�̂����ŁC���Ă͂܂�p���I��ł��������D
�@�E�̓x�����z�\�ɂ��āC�u�x���^�v�u�P��^�v�u����^�v�u���E�Ώ̌^�v�u�E�ɘc��ł���v�u���ɘc��ł���v�u��l�ȕ��z�v�̂����ŁC���Ă͂܂�p���I��ł��������D
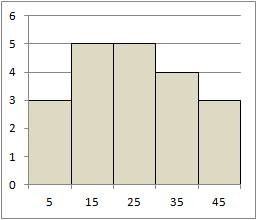 ���t�}������90�x��]����Ɠx�����z�\�ɂȂ�܂�
���t�}������90�x��]����Ɠx�����z�\�ɂȂ�܂�
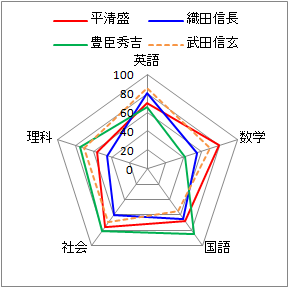

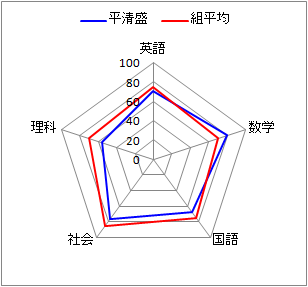
 �p�ꌗ�ł̓^���[�L���itally:�m�����n�L�^����C�W�v����j�łT��\��
�p�ꌗ�ł̓^���[�L���itally:�m�����n�L�^����C�W�v����j�łT��\��