Pythonで整数問題を解く

≪いっしょにPython≫　プログラマーの実験ノート

　このページは，プログラム言語Pythonをこれから学ぼうと考えている筆者の備忘録です．
　そこそこ調べて書いていますが，仕様を精密に調べたものではありません．どちらかと言えば，実装されたPython 3を使ってみてどうなったかということを中心に書いたものです．いわば，実験ノートの記録です．（2019.5.7，Python3.7.3に基づいて作成）

Pythonの練習には，

(1) IDLEというメニューから入って，>>>というプロンプトが表示される状態で使う場合

• 画面の上端がPython 3.7.x Shellとなっていて，２行目がFile, Edit, Shell, Debug, ...となっている
• 1行入力するたびに，エラーを確かめながら処理を進める，対話型インタプリタの形になっている

(2) IDLEというメニューから入って，左上端のFileをクリック→New Fileと進む場合

• 画面の上端がファイル名（初めはUntitled）となっていて，２行目がFile, Edit, format, Run, ...となっている

(3) Python 3.7.x という真っ黒なコマンドプロンプトの画面（ターミナルウィンドウ）から入るもの

の３通りが使えるが，以下は(2)のNew Fileから，テキストエディタを使って，プログラムを書く場合を考える．

Pythonで整数問題を解く(1)

1. 素数の判定と生成

• １よりも大きな整数のうちで，１とその数自身の他に約数をもたない数を素数という．（1は素数に入れない）
• 100以下の素数は，2,3,5,7,11,13,17,19,23,29,31,37,41,43,47, 53,59,61,67,71,73,79,83,89,97 の25個ある．
　ここでは，

・ある正整数nが与えられたとき，その数が素数であるかを判定する関数を作る

・できるだけ多くの素数を作る

ことを目指す．
• 素数判定を素朴に行うには「2以上n未満の整数で割り切れない正の整数nは素数である」と判定すればよい．

== 素数判定1 ==
「2以上n未満の整数で割り切れない正の整数nは素数である」を使って判定する
【例 1.1】

IDLE → New File → Save as .. → Run

def is_prime(n):
    for k in range(2, n):#1
        if n % k == 0:
            return False#2
        else:
            continue #3
    return True #4
print(is_prime(12)) #5
print(is_prime(13)) #5

→
False
True
#1→ range(start, stop)は start≦k<stopの整数列を作る．startは含むがstopは含まれない．したがって，range(2, n)により2≦k≦n−1の整数列ができる．
#2→ n % kでnをkで割った余りが得られるから，n % k == 0すなわち，nがkで割り切れるとき，素数でないと言えるからFalseを返して終了する．
#3→ nがkで割り切れないときは，何も判断せずに次の数を調べに行く(continue)
#4→ forループが#2に至らずに，正常終了したら，n−1以下で割り切れる数はなかったということだから，素数と判断してTrueを返す．
#5→ 結果が分かっているものについて（12は素数でない，13は素数）2，3個の小実験を行い，プログラムが正常に動くことを確かめる．

== 素数の生成1 ==
例1.1の素数判定プログラムを使って，1000未満の素数を列挙する．その際，プログラムの実行速度を測定するために，datetimeモジュールをインポートして，初め（nt1）と終わり（nt2）の時刻を測定し，その時間差（nt2-nt1）を測定する．
【例 1.2】

IDLE → New File → Save as .. → Run

import datetime as dt
dt1 = dt.datetime
nt1 = dt1.now() #1
prime_list = [] #2
def is_prime(n):
    for k in range(2, n):
        if n % k == 0:
            return False
        else:
            continue
    return True
for x in range(2, 1000):
    if is_prime(x) == True:
        prime_list.append(x) #3
nt2 = dt1.now() #4
print(prime_list, '\n', nt2-nt1) #5

→
[2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, 101, 103, 107, 109, 113, 127, 131, 137, 139, 149, 151, 157, 163, 167, 173, 179, 181, 191, 193, 197, 199, 211, 223, 227, 229, 233, 239, 241, 251, 257, 263, 269, 271, 277, 281, 283, 293, 307, 311, 313, 317, 331, 337, 347, 349, 353, 359, 367, 373, 379, 383, 389, 397, 401, 409, 419, 421, 431, 433, 439, 443, 449, 457, 461, 463, 467, 479, 487, 491, 499, 503, 509, 521, 523, 541, 547, 557, 563, 569, 571, 577, 587, 593, 599, 601, 607, 613, 617, 619, 631, 641, 643, 647, 653, 659, 661, 673, 677, 683, 691, 701, 709, 719, 727, 733, 739, 743, 751, 757, 761, 769, 773, 787, 797, 809, 811, 821, 823, 827, 829, 839, 853, 857, 859, 863, 877, 881, 883, 887, 907, 911, 919, 929, 937, 941, 947, 953, 967, 971, 977, 983, 991, 997]
0:00:00.012998
#1→ 初めの時刻を測定する
#2→ prime_listと名付けた空のリストを用意し，見つけた素数をこのリストに順に入れる．
#3→ リストの末尾に要素（x）を１つ追加するには，append(x)とする．
#4→ 最後の時刻を測定する．
#5→ 素数のリストと所要時間を表示しする．

• 上記のプログラムでは，1000未満の素数を約0.013秒で調べているが，これを100万，1億と大きくしていくと途端に所要時間が長くなるので，少しでも改善して，にっこり笑ってできる時間内（数分以内）にできる限り多くの素数列を作れるようにしたい．
• まず，「2以上n未満の整数で割って行く」ことには無駄がある．すなわち､２で割り切れたら，他の偶数でも割り切れることは明らかだから，3以上では割り算は奇数だけにする．判定される数についても同様．
　3以上の奇数を順に並べるには，range(3, n, 2)のように第3引数にstep=2を指定すればよい．
• さらに，ある数nに（1よりも大きい）約数があれば，小さい方の約数mは，ルートn以下になるから，1≦m≦ルートnまでの範囲で割り算をすれば，少し速くなる．

== 素数判定2 ==
「3以上ルートn以下」の「奇数」で割り切れないかどうか調べる
【例 1.3】

IDLE → New File → Save as .. → Run

def is_prime(n):
    for k in range(3, n, 2):
        if n % k == 0:
            return False
        else:
            continue
    return True

== 素数の生成2 ==
上記の例1.3を使って，「3以上ルートn以下」の「奇数」だけを調べる．偶数の2だけは初めに入れておく．
【例 1.4】

IDLE → New File → Save as .. → Run

import datetime as dt
import math as mt
dt1 = dt.datetime
nt1 = dt1.now()
prime_list = [2]
def is_prime(n):
    sq = int(mt.sqrt(n))
    for k in range(3, sq+1, 2): #1
        if n % k == 0:
            return False
        else:
            continue
    return True
for x in range(3, 1000, 2):
    if is_prime(x) == True:
        prime_list.append(x)
nt2 = dt1.now()
print(prime_list, '\n', nt2-nt1)

→ これにより，所要時間は約0.001秒と10分の1ほどに減る．
• nが平方数の場合，ちょうどsqで割り切れるので，rangeのstopはsq+1にしなければならない．

• 2以外の偶数は初めから調べないことにより，上記のプログラムは少し速くなったが，その意味では3の倍数でも，5の倍数でも，…割らないことにすればより速くなる．要するに，その時点までに素数のリストに入ったものでだけ試し割り算を行うことにすれば，もっと早くなるはずである．…2, 3, 5, 7, …で割る．
• 理屈上，これは正しいと考えられるが，大きな時限爆弾も抱えることになる．なぜかというと，この方法で行うには，すでに見つかった素数列をメモリ上に常駐させることになるが，例えば素数50万個のリストとなると，何キロバイトものデータになるので，仮にシステムが使えるメモリが1ギガバイトだとしても，いずれメモリを使い果たして，行き詰まることが予想される．
bull; それはさておき，どのくらいの大きさのデータになるか試してみる値打ちはある．

== 素数判定3 ==
それまでにできた素数で割る
【例 1.5】

IDLE → New File → Save as .. → Run

prime_list = [2,3]
def is_prime(n):
    for k in prime_list[1:]: #3以後で割る
        if n % k == 0:
            return False
        else:
            continue
    return True

== 素数の生成3 ==
【例 1.6】

IDLE → New File → Save as .. → Run

import datetime as dt

dt1 = dt.datetime
nt1 = dt1.now()
prime_list = [2,3]
def is_prime(n):
    for k in prime_list[1:]: #3以後で割る
        if n % k == 0:
            return False
        else:
            continue
    return True
def generate_prime(max1):
    p = 3
    while p < max1:
        p += 2
        if is_prime(p) == True:
            prime_list.append(p)
generate_prime(1000)
nt2 = dt1.now()
print(prime_list,'\n',nt2-nt1)

→ 所要時間は約0.003秒とむしろ遅くなる．
→ 先に述べたように，このやり方では素数リストが大きくなるとメモリを使い果たす可能性もあるので，この方法は捨てる．
• PythonのShellで，結果を直接画面に表示できるのは100行程度までなので，以下においては，テキストファイルに書き込むことにし，結果は外部のエディタで読むことにする．

== 素数の生成4 ==
【例 1.7】

IDLE → New File → Save as .. → Run

import math as mt
import datetime as dt
dt1 = dt.datetime
tn1 = dt1.now()

file1 = open('c:/data/test1.txt','wt')
file1.write('2,3')
def is_prime(p1):
    sq = int(mt.sqrt(p1))
    for n in range(3, sq+1,2):
        if p1 % n == 0:
            return False
        else:
            continue
    return True
def generate_prime3(max1):
    p = 3
    while p < max1:
        p += 2
        if is_prime(p) == True:
            file1.write(','+str(p))
generate_prime3(1000)#1
file1.close()
tn2 = dt1.now()
print(tn2-tn1)

→ ファイル書き込みを行うのでやや遅くなるが，所要時間は約0.004秒になる．
→ この方法で#1の引数を10万，20万，30万，…100万と書き換えると，所要時間：ファイルサイズは各々，0.43秒：55KB，1.08秒：113KB，1.88秒：167KB，…9.43秒：526KBになる．

（1～）
2,3,5,7,11,13,17,19,23,29,31,37,41,43,47,53,59,61,67,71,73,79,83,89,97,…
99707,99709,99713,99719,99721,99733,99761,99767,99787,99793,99809,99817,99823,99829,99833,99839,99859,99871,99877,99881,99901,99907,99923,99929,99961,99971,99989,99991,
（100000～）
100003,100019,100043,100049,100057,100069,100103,100109,100129,100151,…,199501,199523,199559,199567,199583,199601,199603,199621,199637,199657,199669,199673,199679,199687,199697,199721,199729,199739,199741,199751,199753,199777,199783,199799,199807,199811,199813,199819,199831,199853,199873,199877,199889,199909,199921,199931,199933,199961,199967,199999,
（200000～）
200003,200009,200017,200023,200029,200033,200041,200063,200087,200117,…,299479,299501,299513,299521,299527,299539,299567,299569,299603,299617,299623,299653,299671,299681,299683,299699,299701,299711,299723,299731,299743,299749,299771,299777,299807,299843,299857,299861,299881,299891,299903,299909,299933,299941,299951,299969,299977,299983,299993,
（300000～）
300007,300017,300023,300043,300073,300089,300109,300119,300137,…,399739,399757,399761,399769,399781,399787,399793,399851,399853,399871,399887,399899,399911,399913,399937,399941,399953,399979,399983,399989,
（400000～）
400009,400031,400033,400051,400067,400069,400087,400093,400109,…,499903,499927,499943,499957,499969,499973,499979,
（500000～）
500009,500029,500041,500057,500069,500083,500107,500111,…,599537,599551,599561,599591,599597,599603,599611,599623,599629,599657,599663,599681,599693,599699,599701,599713,599719,599741,599759,599779,599783,599803,599831,599843,599857,599869,599891,599899,599927,599933,599939,599941,599959,599983,599993,599999,
（600000～）
600011,600043,600053,600071,600073,600091,600101,600109,600167,600169,…699863,699931,699943,699947,699953,699961,699967,
（700000～）
700001,700027,700057,700067,700079,700081,700087,700099,700103,700109,…799543,799553,799573,799609,799613,799619,799621,799633,799637,799651,799657,799661,799679,799723,799727,799739,799741,799753,799759,799789,799801,799807,799817,799837,799853,799859,799873,799891,799921,799949,799961,799979,799991,799993,799999,
（800000～）
800011,800029,800053,800057,800077,800083,800089,800113,800117,800119,…899447,899467,899473,899477,899491,899519,899531,899537,899611,899617,899659,899671,899681,899687,899693,899711,899719,899749,899753,899761,899779,899791,899807,899831,899849,899851,899863,899881,899891,899893,899903,899917,899939,899971,899981,
（900000～）
900001,900007,900019,900037,900061,900089,900091,900103,900121,…999359,999371,999377,999389,999431,999433,999437,999451,999491,999499,999521,999529,999541,999553,999563,999599,999611,999613,999623,999631,999653,999667,999671,999683,999721,999727,999749,999763,999769,999773,999809,999853,999863,999883,999907,999917,999931,999953,999959,999961,999979,999983

2. 素数定理の実験

• 素数について調べることができるようになったら，整数問題を取り上げてみましょう．
• 素数定理とは，自然数の内で素数がどの位の割合で含まれるかについて述べたもので，

　自然数 $n$ を超えない素数の個数を $\pi (x)$ で表すとき，（この $\pi$ は円周率とは関係ない）

素数を小さい方から並べると2,3,5,7,11,...となるから，
例えば $\pi(2)=1,\hspace{3}\pi(3)=2,\hspace{3}\pi(5)=3,\hspace{3}\pi(7)=4,\hspace{2}\cdots$ などとなる．

　 $n$ 以下の自然数のうちで素数であるものの割合は $\frac{\pi (n)}{n}$ になるが， $n$ が十分大きな自然数であるとき，これがほぼ $\frac{1}{\log_e n}$ に等しいという定理である．

• この定理は，コンピュータを使わずに，数学の定理として1896年に証明されている．
• この定理からは，素数は限りなくあるが，その存在確率 $\frac{\pi (n)}{n}$ はしだいに薄くなるということが分かる．
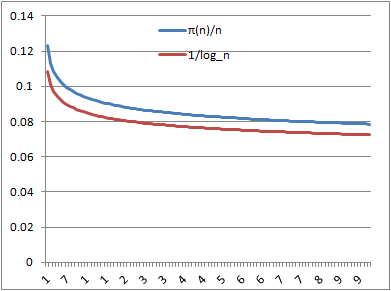
• ここでは，素数の存在確率 $\frac{\pi (n)}{n}$ と $\frac{1}{\log_e n}$ を実際に比較する実験をしてみる．

• データがあまり多くなっても困るので，10000ずつ100組，100万まで求める．（プログラムを簡単にするため，10000を超えるたびに数える）
【例 2.1】

IDLE → New File → Save as .. → Run

import math as mt
import datetime as dt
dt1 = dt.datetime
tn1 = dt1.now()

prime_list = ''
def is_prime(p1):
    sq = int(mt.sqrt(p1))
    for n in range(3, sq+1,2):
        if p1 % n == 0:
            return False
        else:
            continue
    return True
def generate_prime(max1):
    global prime_list
    p = 3
    per10000 = 0
    kosuu = 2
    while p < max1:
        p += 2
        if is_prime(p) == True:
            kosuu += 1
            if int(p/10000) > per10000:
                prime_list += str(kosuu)
		+'\t'+str(p)+'\n'
                per10000 = int(p/10000)                
generate_prime(1001000)
print(prime_list)
tn2 = dt1.now()
print(tn2-tn1)

→ 100組の値を比較すると，次のグラフのようになる．きれいに一致するわけではないが，近づくという感じは分かる．

3. ユークリッドの証明（もどき）

• 素数が無限に多く存在することは，ギリシャ時代から背理法を用いて証明されている．（ユークリッド原論）

　素数が，2,3,5,..., pの有限個だと仮定すると

N = 2·3·5· … ·p +1

のように，すべての素数の積に1を加えた数を考えると，この数Nは2,3,5,..., pのいずれでも割り切れない（1余る）から，pよりも大きい素数である．
　したがって，素数が，2,3,5,..., pの有限個だという仮定が間違っており，素数は無限個ある．

• この証明は多くの教科書に記載されており，信頼できるものである．しかし，次のように早合点してはいけない．
（あわて者の解釈）「N = 2·3·5· … ·p+1は素数である」
　ユークリッドの証明は「素数が，2,3,5,..., pの有限個だと仮定すると，N = 2·3·5· … ·p+1が素数になる」と述べているが，実際には,素数は無限個あるから，この仮定が間違っており，「N = 2·3·5· … ·p+1が素数になる」という結論は，正しいことも間違っていることもある．（仮定が間違っていれば，結論が何であっても真）
• 以下においては，2+1, 2·3+1, 2·3·5+1, 2·3·5·7+1, … が実際に素数になるかどうかを調べてみる．

• 100までの素数について，ユークリッドの証明の真似をして作った数が素数になるかどうかを調べる．
• 筆者のパソコンでは，61までは0.17秒と一瞬でできるが，67まで含めるといつまで経ってもできない．（61までで積が24桁の整数になり，これよりも大きくなるとマシンのパワーに無理がある.Maximaで求めると，残りの97まではすべて合成数になることが分かる）
【例 3.1】

IDLE → New File → Save as .. → Run

import math as mt
import datetime as dt
dt1 = dt.datetime
tn1 = dt1.now()
prime_list = [2,3,5,7,11,13,17,19,23,29,31,37,
41,43,47,53,59,61]#,67,71,73,79,83,89,97]
ok_list =[]
okN_list = []
no_list =[]
noN_list = []
def is_prime(p1):
    sq = int(mt.sqrt(p1))
    for n in range(3, sq+1,2):
        if p1 % n == 0:
            return n
        else:
            continue
    return True
def product_plus1():
    global prime_list
    for n in range(len(prime_list)):
        N = 1
        k = 0
        for k in range(n+1):
            N *= prime_list[k]
        N += 1
        if is_prime(N) == True:
            ok_list.append(prime_list[n])
            okN_list.append(N)
        else:
            no_list.append(prime_list[n])
            noN_list.append(str(N)+':'
	    +str(is_prime(N)))
product_plus1()
print(ok_list,'\n',okN_list,'\n',no_list,noN_list)
tn2 = dt1.now()
print(tn2-tn1)

→
Nが素数となるpの値は
[2, 3, 5, 7, 11, 31]
そのときのNの値は
[3, 7, 31, 211, 2311, 200560490131]
Nが素数とならないpの値は
[13, 17, 19, 23, 29, 37, 41, 43, 47, 53, 59, 61]
そのときのNの値，および１つの約数は
['30031:59', '510511:19', '9699691:347', '223092871:317', '6469693231:331', '7420738134811:181', '304250263527211:61', '13082761331670031:167', '614889782588491411:953', '32589158477190044731:73', '1922760350154212639071:277', '117288381359406970983271:223']
→ p=13の場合を考えてみると，N=2·3·5·7·11·13 + 1=30031=59·509となって「自分（13）よりも大きな素数で割り切れる」ところがミソ．
　もう1つ例： p=17の場合を考えてみると，N=2·3·5·7·11·13·17 + 1=510511=19·97·277となって「自分（17）よりも大きな素数で割り切れる」

4. 連続する合成数

• 素数でないものは合成数と呼ばれる．
• 素数が簡単に求められるようになると，ある数から合成数が続くことはあるか？という問題に答えられるようになる．
• 理屈上は，以下のように「どんな大きな個数でも合成数が続く」ようにできる．

n! = 1·2·3· … ·(n−1)·n は，2,3,4, … nのどれでも割り切れるから
n!+2 は2で割り切れる．n!+3は3で割り切れる。n!+4は4で割り切れる．… n!+nはｎで割り切れる．したがって，n!+2からn!+nの連続するn−1個の数はすべて合成数である．
nを大きくとれば，限りなく大きな区間で合成数が連続するようにできる．

• 理屈上は，上記の通りであるが，家庭用パソコンでは20!=2432902008176640000でも20桁の数になり，それ以上大きくすると近似計算にされてしまうおそれがある．そこで，実際の素数列で，隣り合う素数の間隔（この間隔−1が連続する合成数）がどうなっているか調べてみる．
　例えば，2,3,5,7,11,13,17,19,23,29 において間隔が1のものは2,3の1組だけあり，23と29の間隔は6である．

• 素数のリストをp_list，その間隔のリストをd_list，各々の間隔となる回数（度数）のリストをd_countとし，上限を#1の箇所で，10000, 100000, 1000000とした場合を見てみる．
【例 4.1】

IDLE → New File → Save as .. → Run

import math as mt
import datetime as dt

dt1 = dt.datetime
tn1 = dt1.now()
p_list = [2,]
d_list = []
d_count =[[1,1],]
def is_prime(p1):
    sq = int(mt.sqrt(p1))
    for n in range(3, sq+1,2):
        if p1 % n == 0:
            return False
        else:
            continue
    return True
def make_prime(max1):
    global p_list
    for m in range(3, max1+1, 2):
       if is_prime(m) == True:
           p_list.append(m)
make_prime(10000)#1
for n in range(len(p_list)-1):
    d_list.append(p_list[n+1]-p_list[n])
for x in range(2,max(d_list)+1,2):
    count1 = d_list.count(x)
    d_count.append([x, count1])
print(d_count)
tn2 = dt1.now()
print(tn2-tn1)

→
[[1, 1], [2, 205], [4, 202], [6, 299], [8, 101], [10, 119], [12, 105], [14, 54], [16, 33], [18, 40], [20, 15], [22, 16], [24, 15], [26, 3], [28, 5], [30, 11], [32, 1], [34, 2], [36, 1]]
1万, 10万, 100万とした場合の間隔の度数は，次のグラフのようになる．

• 100万まで求める所要時間は約9秒であるが，1000万は長くなるので避けたい．
• 1万まで, 10万まで, 100万までのいずれの場合も，隣り合う素数の間隔が6となる（合成数が5個続く）頻度が最も高い．
• 100以下で合成数が連続する最長のものは，24,25,26,27,28の5個（同じ長さのものがあれば小さい方を示す．以下同様）．
10000以下で合成数が連続する最長のものは，888～906の19個
［888=2³×3×37, 889=7×127, 890=2×5×89, 891=3⁴×11, 892=2²×223, 893=19×47, 894=2×3×149, 895=5×179, 896=2⁷×7, 897=3×13×23, 898=2×449, 899=29×31, 900=2²×3²×5², 901=17×53, 902=2×11×41, 903=3×7×43, 904=2³×113, 905=5×181, 906=2×3×151］
10000以下で合成数が連続する最長のものは9552～9586までの35個，100000以下で合成数が連続する最長のものは31398～31468の71個，1000000以下で合成数が連続する最長のものは492114～492226までの113個

5. ベルトラン・チャビシャフの定理

• ベルトラン・チャビシャフの定理「nを正の整数とするとき，n<p≦2nとなる素数pが存在する」
　この定理は，数学的に証明されているが，高校レベルの初等的な方法で証明するのは難しい．
• 100と200の間，1000と2000の間のように，nが大きくなれば間隔が広がる．これほど広い範囲に素数が１つもないなどということはあり得ないから，この定理が成り立つのは，至って当然だと考えられる．

【例 5.1】

IDLE → New File → Save as .. → Run

import math as mt
import datetime as dt

dt1 = dt.datetime
tn1 = dt1.now()

def is_prime(p1):
    sq = int(mt.sqrt(p1))
    for n in range(3, sq+1,2):
        if p1 % n == 0:
            return False
        else:
            continue
    return True
def n_to_2n(n):
    for x in range(n+1, 2*n+1):
        if is_prime(x) == True:
            return x
    return -x
for n in range(1, 100000):#1
    if n_to_2n(n) < 0:
        print(n)
tn2 = dt1.now()
print(tn2-tn1)

→ 所要時間約3.9で100000まで成り立つことが示される．#1の引数を書き換えると範囲を変えられる．
→ 何も出力がないから，プログラムが間違っているのか，正しいのか不気味なプログラムになる．

6. ルジャンドル予想

• 「nを正の整数とするとき，n²<p<(n+1)²となる素数pが存在する」（ルジャンドル予想）
　この予想は，証明も反証もされていない．
(1) プログラムを使って，100万程度まで成立することを示したい．
(2) もっと狭い範囲の予想に変えられるか調べる．

上記の(1)を実際に確かめる
【例 6.1】

IDLE → New File → Save as .. → Run

import math as mt
import datetime as dt

dt1 = dt.datetime
tn1 = dt1.now()

def is_prime(p1):
    sq = int(mt.sqrt(p1))
    for n in range(3, sq+1,2):
        if p1 % n == 0:
            return False
        else:
            continue
    return True
def sq_to_next(n):
    for x in range(n**2+1, (n+1)**2):#1
        if is_prime(x) == True:
            return x
    return 0
for n in range(1, 10000):#2
    if sq_to_next(n) == 0:
        print(n)
tn2 = dt1.now()
print(tn2-tn1)

→ 約7.4秒で，n=10000，すなわちn²が1億の場合まで成り立つことが言える．#2の箇所でn=1000すなわちn²が100万の場合を調べるには，約0.087秒でできる．
• (2)の問題：「n²<p<(n+1)²」よりも厳しい条件，例えば「n²<p<n²+n+1」にしても同様に成り立つ．

7. ゴールドバッハ予想

• ゴールドバッハ予想とは「4よりも大きな偶数は，２つの（奇）素数の和で表される」という予想で，証明も反証もされていない．
• 例えば，6=3+3, 8=5+3, … ,100=97+3
• 素数は小さい方が密で，大きくなると薄くなる傾向があるので，この予想は「小さい方が密である」ことが主な原因ではないかと見当を付けて，与えられた数nの下にある素数Nに対して，小さな素数を順に足して一致すれば終了，和がnを超えてしまえばNを変える方法で調べた．

【例 7.1】

IDLE → New File → Save as .. → Run

import math as mt
import datetime as dt

dt1 = dt.datetime
tn1 = dt1.now()
prime_list = [2,]#1
count_dic = dict()
def is_prime(p1):
    sq = int(mt.sqrt(p1))
    for n in range(3, sq+1,2):
        if p1 % n == 0:
            return False
        else:
            continue
    return True
def generate_prime(max1):
    global prime_list
    for n in range(3, max1, 2):
        if is_prime(n) == True:
            prime_list.append(n)
def is_gold(n):
    L = len(prime_list)
    for p in range(L):
        if prime_list[p] < n:
            continue
    N = p
    for m in range(N, 0, -1):
        for k in range(1, L):
            if (prime_list[m]+prime_list[k]) > n:
                break
            if (prime_list[m]+prime_list[k]) == n:
                return prime_list[k]
            else:
                continue
    return False
num1 = 20000 ###
generate_prime(num1)

for n in range(6, num1, 2):
    k = is_gold(n)
    if k == False:
        print(n)
    else:
        value1 = count_dic.get(k, None)
        if value1 == None:
            count_dic[k] = 1
        else:
            count_dic[k] +=1
count_list = sorted(list(count_dic))
count_list2
 = list(map(lambda x:(x,count_dic[x]), count_list))
print(count_list2)
tn2 = dt1.now()
print(tn2-tn1)

→
小さい方　頻度数　百分率
3　2260　22.6%
5　1918　19.2%
7　1575　15.8%
11　1053　10.5%
13　803　8.0%
17　525　5.3%
19　497　5.0%
23　304　3.0%
29　215　2.2%
31　248　2.5%
37　120　1.2%
41　101　1.0%
…
…
139　5　0.1%
151　2　0.0%
157　1　0.0%
173　2　0.0%
→ 20000未満の偶数の内で2,4を除く9997個の偶数で，ゴールドバッハの予想を満たす2つの偶数の組を調べると，小さい方が1桁で成り立つものが57.5%，2桁まで取れば99.8%になる．運悪く大きくなる場合でも，173になる．これにより，「ほとんどの場合」，ゴールドバッハの予想が成り立つのは，単に「小さい方の素数が密だから」と言えそうだ．すべての場合とは言い切れないのが惜しい．（証明の代わりにはならない）

8. 双子素数の問題

• 双子素数とは，3と5，5と7，11と13のように１つおきに並んだ素数のことをいう．
• 数学的には「双子素数は無限にある」と予想されているが，その証明はまだできていない．
　このような整数問題をプログラミング教材で取り上げる場合は，「コンピュータを使って，人間の代わりに証明してみよう」とまでは中々行かない．無限にあることの証明までは難しくても，「100万までの整数については成り立つ」「10億までの整数については成り立つ」「1兆までの整数については成り立つ」のように有限の巨大数を指定してその範囲までは成り立つことを，言わば「コンピュータによる力仕事で」「体力勝負で」真正面から示すことならできる．
• このような限定的な証明は，数学における「無限にある」の証明にとって代わるものではないが，とても大きな数まで成り立つという事実があれば，本来の数学的な予想にも信頼性が高くなり「証明方法はまだ分からないが，おそらく正しい」だろうなというレベルに達する．

• 2と3を除けば，2の倍数と3の倍数は素数でないから，整数を6で割ったときの余りで分類したとき，6k, 6k+1, 6k+2, 6k+3, 6k+4, 6k+5のうちで素数になる可能性のあるものは，6k+1と6k+5だけです．
• そこで，双子素数があるとすれば6k±1の組です．
• 次のプログラムで，#1のところの引数を書き換えると，その数よりも大きな双子素数があれば表示されます．
【例 8.1】

IDLE → New File → Save as .. → Run

import math as mt
import datetime as dt
dt1 = dt.datetime
tn1 = dt1.now()
def is_prime(p1):
    sq = int(mt.sqrt(p1))
    for n in range(3, sq+1,2):
        if p1 % n == 0:
            return False
        else:
            continue
    return True
def twin_prime(max1):
    p6 = int(max1/6)
    for k in range(p6, p6+1000):
        x = 6*k-1
        if (is_prime(x) == True) \
	    and (is_prime(x+2) == True):
            print(x, x+2)
            break
twin_prime(10000000000000) #1
tn2 = dt1.now()
print(tn2-tn1)

→ 10000000001267 10000000001269
→ 約14秒で10兆（10¹³）よりも大きな双子素数が存在すること，および実際の値を示すことができる．（100万のレベルなら一瞬）
• wikipediaを見れば，双子素数についての最近の情報が分かる．専門家が並列コンピュータなどを使って高速計算したものは巨大なもので，家庭用パソコンではとても対抗できない．

9. 素数の逆数の和

• 素数の逆数の和とは，
$\frac{1}{2}+\frac{1}{3}+\frac{1}{5}+\hspace{2}\cdots\hspace{2}+\frac{1}{97}$
のように，各素数の逆数を加えたもので，この和が有限の値に収束するか，それとも限りなく大きくなるかという点に興味がある．
• 高校数学の基本を簡単に振り返ると，n以下のすべての自然数の逆数の和は
$\frac{1}{1}+\frac{1}{2}+\frac{1}{3}+\hspace{2}\cdots\hspace{2}+\frac{1}{n}\gt\log_e(n+ 1)$

となって， $n\rightarrow \infty$ のとき $\log_e(n+ 1)\rightarrow \infty$ となるから，
素数が自然数と同じくらい濃く分布していると，その逆数の和は収束せずに無限に大きくなる．
• これが，自然数の半分（例えば偶数）くらいの濃さ，10に１つ（例えば10の倍数）くらいの濃さで分布していても
$\frac{1}{2}+\frac{1}{4}+\frac{1}{6}+\hspace{2}\cdots\hspace{2}+\frac{1}{2n}\gt\frac{1}{2}\log_e(n+ 1)\rightarrow\infty$
$\frac{1}{10}+\frac{1}{20}+\frac{1}{30}+\hspace{2}\cdots\hspace{2}+\frac{1}{10n}\gt\frac{1}{10}\log_e(n+ 1)\rightarrow\infty$
となって，単に定数倍（1次関数的に）薄いだけでは，逆数の和は収束しない．
• 他方で，2.素数定理の箇所で述べたように，素数の分布の濃さは $\frac{1}{\log_e n}$ に近く，ｎが大きくなるにつれて薄くなっている．
　他の例で言えば，次の和は収束する．（n²のレベルで薄くなっていけば，逆数の和は収束する）
$\frac{1}{1}+\frac{1}{4}+\frac{1}{9}+\hspace{2}\cdots\hspace{2}+\frac{1}{n^2}$
$=\frac{1}{1^2}+\frac{1}{2^2}+\frac{1}{3^2}+\hspace{2}\cdots\hspace{2}+\frac{1}{n^2}\lt 2$
• それでは，実際に素数の逆数の和は，収束するのか，どのレベルで薄くなっていくのか，実験で調べる．

• 次の###の箇所で上限を定めて，10分割で逆数の和を求める
【例 9.1】

IDLE → New File → Save as .. → Run

import math as mt
import datetime as dt

dt1 = dt.datetime
tn1 = dt1.now()
def is_prime(p1):
    sq = int(mt.sqrt(p1))
    for n in range(3, sq+1,2):
        if p1 % n == 0:
            return False
        else:
            continue
    return True
def inv_plus(max1):
    sum1 = 1/2
    for x in range(3, max1, 2):
        if is_prime(x) == True:
            sum1 += 1/x
        if x % int(max1/10) == 1:
            print(x,'\t',sum1)
max1 = 5000000 ###
inv_plus(max1)

→
500001 2.835931891900168
1000001 2.8873280995676938
1500001 2.9162751004738183
2000001 2.936292491741523
2500001 2.951534114473346
3000001 2.963841640699352
3500001 2.974120794193232
4000001 2.9829338291949576
4500001 2.990661369092672

• 得られた観測データをExcelの散布図→近似曲線の追加→数式を表示などで調べると，図のようになる．
• この近似の決定係数（R²）は0.9995と非常に高く，ほとんど正確な近似曲線だと考えられる．
上記プログラムのmax1を大きくすると，y=0.067ln(x)+1.964のln(x)の係数はしだいに小さくなり，定数項はしだいに大きくなるが，傾向としてはあまり変わらない．
• 以上から，素数の逆数の和は収束せず，限りなく大きくなると予想できる．
• では，素数の分布は $n^1\lt n^{\alpha}\lt n^2$ のどれくらいのレベルで「薄くなって」行くのかという議論ができる．

○== メニューに戻る ==

≪いっしょにPython≫ プログラマーの実験ノート

Pythonで整数問題を解く(1)

1. 素数の判定と生成

2. 素数定理の実験

3. ユークリッドの証明（もどき）

4. 連続する合成数

5. ベルトラン・チャビシャフの定理

6. ルジャンドル予想

7. ゴールドバッハ予想

8. 双子素数の問題

9. 素数の逆数の和

≪いっしょにPython≫　プログラマーの実験ノート