三角形の面積の二等分線

== 三角形の面積の二等分線 ==
○三角形の面積は

（面積）＝（底辺）×（高さ）÷2

の公式で求められます．
　次の図のように，△ABCの頂点Aから対辺BCの中点（真ん中の点，１対１に内分する点）Dに線分ADをひくと，△ABDと△DCAとは，底辺が等しく，高さが共通になるから，これら２つの三角形の面積は等しくなります．（高さは底辺と垂直（直角）な線分で測ります）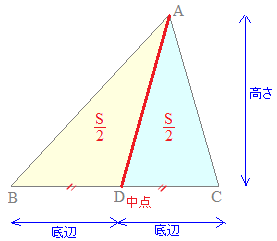

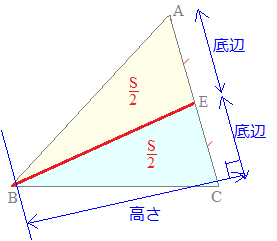次の図のように，頂点Bから対辺CAの中点Eに線分BEをひいた場合にも，同様にして△BCEと△BAEの面積は等しくなります．

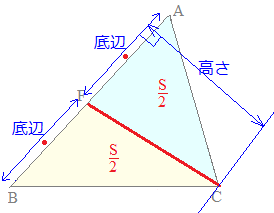
さらに，頂点Cから対辺ABの中点Fに線分CFをひいた場合にも，同様にして△CAFと△CBFの面積は等しくなります．

【要点】
　三角形の頂点から対辺の中点にひいた線分は，三角形の面積を二等分する

【例１】
　3点A(3, 4), B(1, 2), C(5, 0)を頂点とする△ABCがある．
(1)　辺BC上に点Dをとって，線分ADが△ABCの面積を二等分するようにするとき，点Dの座標を求めてください．

(2)　辺CA上に点Eをとって，線分BEが△ABCの面積を二等分するようにするとき，点Eの座標を求めてください．

(1)　辺AB上に点Fをとって，線分CFが△ABCの面積を二等分するようにするとき，点Fの座標を求めてください．

【ポイント】
　点P(a, b)と点Q(s, t)の中点の座標は
( $\frac{a+ s}{2}$ , $\frac{b+ t}{2}$ )
※x座標とx座標からx座標を作る，y座標とy座標からy座標を作る．
※１つの座標のx座標とy座標を混ぜてはいけない．

（解答）
(1)
　B(1, 2), C(5, 0)の中点を点Dとすればよいから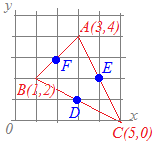

Dのx座標は
$\frac{1+ 5}{2}=3$
y座標は
$\frac{2+ 0}{2}=1$
したがって
D(3, 1)…（答）

点の名前とその座標の間には何も入れずにD(3, 1)のように書きます．
D=(3, 1)のようには書かないので注意しましょう．

(2)
　同様にして
$\frac{3+ 5}{2}=4$ ， $\frac{4+ 0}{2}=2$
だから
E(4, 2)…（答）
(3)
　同様にして
$\frac{3+ 1}{2}=2$ ， $\frac{4+ 2}{2}=3$
だから
F(2, 3)…（答）

【例２】
　3点A(3, 2), B(0, 0), C(4, 0)を頂点とする△ABCがある．
頂点Aを通り△ABCの面積を二等分する直線の方程式を求めてください．

【ポイント】
　B(0, 0), C(4, 0)の中点D(2, 0)と頂点A(3, 2)を通る直線の方程式を
y=ax+b
とおいて，この直線がD(2, 0)とA(3, 2)を通るように，a, bの値を求めます．

（解答）
B(0, 0), C(4, 0)の中点をDとおくと，Dの座標は 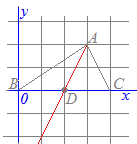$(\frac{0+ 4}{2}, \frac{0 + 0}{2})$ によりD(2, 0)

D(2, 0)と頂点A(3, 2)を通る直線の方程式を
y=ax+b
とおくと，この直線がD(2, 0)を通るから
0=2a+b…(1)
A(3, 2)を通るから
2=3a+b…(2)
(1)(2)の連立方程式を解いてa, bの値を求める．
(2)−(1)
a=2
これを(1)に代入すると
0=4+b
b=−4
ゆえに
y=2x−4…（答）

【問題１】
　3点A(3, 5), B(1, 1), C(5, 0)を頂点とする△ABCがある．
頂点Cを通り△ABCの面積を二等分する直線の方程式を求めてください．解説

$y=x$ $y=x+ 5$

$y=-x+ 5$ $y=\frac{1}{2}x+ \frac{1}{2}$

A(3, 5), B(1, 1)の中点をDとするとDの座標は
$(\frac{3+ 1}{2},\frac{5+ 1}{2})=(2,3)$
2点D(2, 3), C(5, 0)を通る直線の方程式を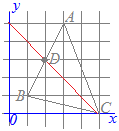

y=ax+b
とおいて，a, bを求める．
D(2, 3)を通るから
3=2a+b…(1)
C(5, 0)を通るから
0=5a+b…(2)
a, bの連立方程式(1)(2)を解く．
(2)−(1)
−3=3a
a=−1
これを(1)に代入
b=5
ゆえに
y=−x+5…（答）

【問題２】
　3点A(3, 5), B(−2, 3), C(4, −1)を頂点とする△ABCがある．
頂点Aを通り△ABCの面積を二等分する直線の方程式を求めてください．解説

y=2x+1 y=2x−1

y=−2x+1 y=−2x−1

B(−2, 3), C(4, −1)の中点をDとするとDの座標は
$(\frac{-2+ 4}{2},\frac{3+(-1)}{2})=(1,1)$
2点D(1, 1), A(3, 5)を通る直線の方程式を
y=ax+b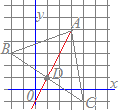

とおいて，a, bを求める．
D(1, 1)を通るから
1=a+b…(1)
A(3, 5)を通るから
5=3a+b…(2)
a, bの連立方程式(1)(2)を解く．
(2)−(1)
4=2a
a=2
これを(1)に代入
b=−1
ゆえに
y=2x−1…（答）

【問題３】
　3点A(−1, 2), B(4, −3), C(3, 4)を頂点とする△ABCがある．
頂点Bを通り△ABCの面積を二等分する直線の方程式を求めてください．解説

y=2x−3 y=2x−1

y=−2x+3 y=−2x+5

A(−1, 2), C(3, 4)の中点をDとするとDの座標は
$(\frac{-1+ 3}{2},\frac{2+ 4}{2})=(1,3)$
2点D(1, 3), B(4, −3)を通る直線の方程式を
y=ax+b
とおいて，a, bを求める．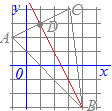

D(1, 3)を通るから
3=a+b…(1)
B(4, −3)を通るから
−3=4a+b…(2)
a, bの連立方程式(1)(2)を解く．
(2)−(1)
−6=3a
a=−2
これを(1)に代入
b=5
ゆえに
y=−2x+5…（答）

【例３】
　3点A(0, 4), B(0, 0), C(3, 0)を頂点とする△ABCがある．
線分BC上の点D(2, 0)を通り△ABCの面積を二等分する直線と線分ABの交点をEとするとき，点Eのy座標を求めてください

【ポイント】
三角形の面積は
（面積）＝（底辺）×（高さ）÷2
の公式で求められるので，
（面積）と（底辺）の長さが決まっていたら，（高さ）が求まる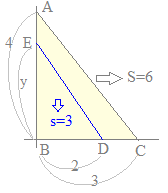

（解答）
△ABCの面積は
$\frac{3 \times 4}{2}=6$
△EBDの面積は
$\frac{2 \times y}{2}$
△ABCの面積を二等分しているのだから
$\frac{2 \times y}{2}=3$
$y=3$ …（答）

【例４】
　3点A(2, 4), B(0, 0), C(6, 0)を頂点とする△ABCがある．
線分BC上の点D(4, 0)を通り△ABCの面積を二等分する直線と線分ABの交点Eの座標を求めてください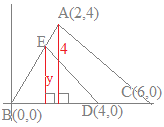

（解答）
△ABCの面積は
$\frac{6 \times 4}{2}=12$
Eのy座標をyで表すと
△EBDの面積は
$\frac{4 \times y}{2}=2y$
△ABCの面積を二等分しているのだから
$2y=6$
$y=3$
ABの直線の方程式は
$y=2x$
だから， $y=3$ のとき
$3=2x$
$x=\frac{3}{2}$
ゆえに
$E(\frac{3}{2},3)$ …（答）

【ポイント】
　底辺がx軸上にあれば，高さはy座標

【問題４】
　3点A(0, 5), B(0, 0), C(6, 0)を頂点とする△ABCがある．
線分BC上の点D(5, 0)を通り△ABCの面積を二等分する直線と線分ABの交点をEとするとき，点Eのy座標を求めてください解説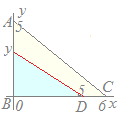

1 2 3 4

△ABCの面積は
$\frac{6 \times 5}{2}=15$
△EBDの面積は
$\frac{5 \times y}{2}$
△ABCの面積を二等分しているのだから
$\frac{5y}{2}=\frac{15}{2}$
$y=3$ …（答）

【問題５】
　3点A(0, 4), B(0, 0), C(5, 0)を頂点とする△ABCがある．
線分AB上の点D(0, 3)を通り△ABCの面積を二等分する直線と線分BCの交点をEとするとき，点Eのx座標を求めてください解説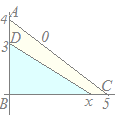

$\frac{5}{3}$ $\frac{7}{3}$ $\frac{8}{3}$ $\frac{10}{3}$ $\frac{11}{3}$

△ABCの面積は
$\frac{5 \times 4}{2}=10$
△EBDの面積は
$\frac{x \times 3}{2}$
△ABCの面積を二等分しているのだから
$\frac{3x}{2}=5$
$x=\frac{10}{3}$ …（答）

【問題６】
　3点A(3, 6), B(0, 0), C(4, 0)を頂点とする△ABCがある．
線分BC上の点D(3, 0)を通り△ABCの面積を二等分する直線と線分ABの交点をEとするとき，点Eの座標を求めてください解説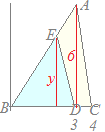

$(1,2)$ $(\frac{3}{2},3)$ $(2,4)$ $(\frac{5}{2},5)$

△ABCの面積は
$\frac{6 \times 4}{2}=12$
Eのy座標をyで表すと
△EBDの面積は
$\frac{3 \times y}{2}$
△ABCの面積を二等分しているのだから
$\frac{3y}{2}=6$
$y=4$
ABの直線の方程式は
$y=2x$
だから， $y=4$ のとき
$4=2x$
$x=2$
ゆえに
$E(2,4)$ …（答）

【問題７】
　3点A(4, 4), B(0, 0), C(5, 0)を頂点とする△ABCがある．
線分BC上の点D(4, 0)を通り△ABCの面積を二等分する直線と線分ABの交点をEとするとき，点Eの座標を求めてください解説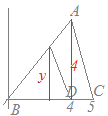

$(\frac{3}{2},\frac{5}{2})$ $(\frac{5}{2},\frac{3}{2})$ $(\frac{5}{2},\frac{5}{2})$ $(\frac{7}{2},\frac{5}{2})$

△ABCの面積は
$\frac{5 \times 4}{2}=10$
Eのy座標をyで表すと
△EBDの面積は
$\frac{4 \times y}{2}=2y$
△ABCの面積を二等分しているのだから
$2y=5$
$y=\frac{5}{2}$
ABの直線の方程式は
$y=x$
だから， $y=\frac{5}{2}$ のとき
$x=\frac{5}{2}$
ゆえに
$E(\frac{5}{2},\frac{5}{2})$ …（答）

【例５】
　3点A(0, 3), B(0, 0), C(4, 4)を頂点とする△ABCがある．
線分BC上の点P(3, 3)を通り△ABCの面積を二等分する直線と線分ABの交点をQとするとき，点Qのy座標を求めてください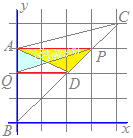

【考え方１】
○BCの中点D(2, 2)と頂点Aを結ぶ線分ADは△ABCの面積を二等分する．
○そうすると，△PABの面積は△ABCの面積の半分よりも△PADの分だけ大きくなっている．
○△PADをPAを底辺として高さを変えずに等積変形すると△PAD=△PAQとなるように点Qを定めることができる．
○そこで，△PABから△PAQを取り除いたもの，すなわち△PQBが△ABCの面積を二等分することになる．

（解答）
　BCの中点D(2, 2)と点A(0, 3), P(3, 3)でできる△PADを，PAを底辺として高さを変えない等積変形を行う．
　Dを通りPAと平行な直線とABとの交点をQとおくと，△PAD=△PAQとなる．
　PAはx軸に平行だからDQもx軸に平行（y座標を変えない）に取ると
Q(0, 2)…（答）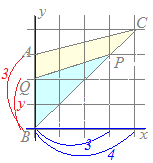

【考え方2】

この部分は中3の相似図形の性質を習ってからの方がよく分かるが，内容は小学校でも習う

○Q(0, y)とおき，AB, QBを底辺と考えると，底辺の長さの比はAB:QB=3:y
○高さの比はC, Pのx座標の比になるから4:3
○三角形の面積は
（面積）＝（底辺）×（高さ）÷2
だから，面積の比は
（底辺1）×（高さ1）:（底辺2）×（高さ2）

（解答）
　Q(0, y)とおくと，
底辺の比は3:y
高さの比は4:3
$\frac{y}{3}\times \frac{3}{4}=\frac{1}{2}$
よりy=2
Q(0, 2)…（答）

【例６】
　3点A(3, 3), B(−1, −1), C(5, 2)を頂点とする△ABCがある．
線分BC上の点P(3, 1)を通り△ABCの面積を二等分する直線と線分ABの交点をQとするとき，点Qの座標を求めてください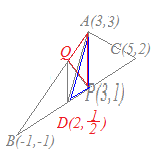

【考え方１】
○BCの中点 $D(2,\frac{1}{2})$ と頂点Aを結ぶ線分ADは△ABCの面積を二等分する．
○そうすると，△PABの面積は△ABCの面積の半分よりも△PADの分だけ大きくなっている．
○△PADをPAを底辺として高さを変えずに等積変形すると△PAD=△PAQとなるように点Qを定めることができる．
○そこで，△PABから△PAQを取り除いたもの，すなわち△PQBが△ABCの面積を二等分することになる．

（解答）
　BCの中点 $D(\frac{-1+ 5}{2},\frac{-1+ 2}{2})$ すなわち $D(2,\frac{1}{2})$ と点A(3, 3), P(3, 1)でできる△PADを，PAを底辺として高さを変えない等積変形を行う．
　Dを通りPAと平行な直線とABとの交点をQとおくと，△PAD=△PAQとなる．
　PAはy軸に平行だからDQもy軸に平行（x座標を変えない）に取る．
Qのx座標はDと同じ2になり,Qは直線AB:y=x上の点だから，Qのy座標は2
Q(2, 2)…（答）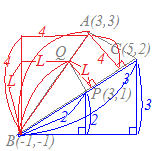

【考え方2】

この部分は中3の相似図形の性質を習ってからの方がよく分かるが，内容は小学校でも習う

○底辺の比はCB:PB=3:2
○高さの比はAB:QB=4:L

長さは各々3,2,4,Lではない．比が3:2, 4:Lだということに注意

○面積の比は
$\frac{2}{3}\times \frac{L}{4}=\frac{1}{2}$
とおくと
L=3
y座標は2になる．

（解答）
AB:QB=4:Lとおくと，
底辺の比は3:2
高さの比は4:L
$\frac{2}{3}\times \frac{L}{4}=\frac{1}{2}$
よりL=3
y座標の差を考えるとAB:QB=3−(−1):y−l(−1)=4:y+1
これが4:3になるのだからy=2
Qは直線AB:y=x上の点だからx=2
Q(2, 2)…（答）

【問題８】
　3点A(2, 4), B(0, 0), C(6, 0)を頂点とする△ABCがある．
線分AC上の点P(3, 3)を通り△ABCの面積を二等分する直線と線分BCの交点をQとするとき，点Qの座標を求めてください解説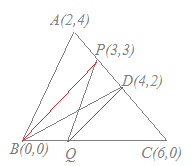

(1, 0) (2, 0) (3, 0) (4, 0)

　ACの中点D(4,2)と頂点Bを結ぶ線分DBは△ABCの面積を二等分する．
　△PBCの面積は△ABCの半分よりも△PBDの分だけ多い．
　△PBDを底辺PBを共通として高さを変えずに等積変形して，頂点Dを移動させて線分BC上にきたとき，その点をQとすると，△PBD=△PBQとなり，△PQCの面積は△ABCの半分になる．
　P(3,3), B(0,0)を通る直線の傾きは1だから，点D(4,2)を通り，傾き1の直線とBCの交点を求めるとよい．
　DQの方程式は，傾きが1だから
y=x+b
とおける．これがD(4,2)を通るから
b=−2
y=x−2とBC:y=0との交点を求めると
Q(2, 0)…（答）
（別解） - - - - - - - -
斜辺の長さをx座標の差で比較すると
$\frac{PC}{AC}=\frac{6-3}{6-2}=\frac{3}{4}$
Qの座標を(x, 0)とおくと
$\frac{QC}{BC}=\frac{6-x}{6}$
$\frac{3}{4}\times \frac{6-x}{6}=\frac{1}{2}$
より
3(6−x)=12
18−3x=12
3x=6
x=2
ゆえに
Q(2, 0)…（答）

【問題９】
　3点A(3, 6), B(0, 0), C(8, 4)を頂点とする△ABCがある．
線分BC上の点P(6, 3)を通り△ABCの面積を二等分する直線と線分ABの交点をQとするとき，点Qの座標を求めてください解説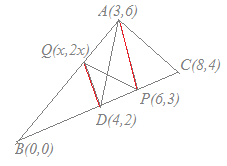

(1, 2) (2, 4) (3, 3) (5, 5)

　BCの中点D(4,2)と頂点Aを結ぶ線分DAは△ABCの面積を二等分する．
　△PABの面積は△ABCの半分よりも△PADの分だけ多い．
　△PADを底辺PAを共通として高さを変えずに等積変形して，頂点Dを移動させて線分AB上にきたとき，その点をQとすると，△PAD=△PAQとなり，△PQBの面積は△ABCの半分になる．
　P(6,3), A(3,6)を通る直線の傾きは−1だから，点D(4,2)を通り，傾き−1の直線とABの交点を求めるとよい．
　DQの方程式は，傾きが−1だから
y=−x+b
とおける．これがD(4,2)を通るから
b=6
y=−x+6
次に，ABの方程式はy=2x
これらの交点を求めると
Q(2, 4)…（答）
（別解） - - - - - - - -
斜辺の長さをx座標の差で比較すると
$\frac{PB}{CB}=\frac{6}{8}=\frac{3}{4}$
Qの座標を(x, 2x)とおくと
$\frac{QB}{AB}=\frac{x}{3}$
$\frac{3}{4}\times \frac{x}{3}=\frac{1}{2}$
より
x=2
ゆえに
Q(2, 4)…（答）