三角形の等積変形

== 三角形の等積変形 ==
○図形の面積を変えずに形を変えることを「等積変形」といいます．
○三角形の面積は

（面積）＝（底辺）×（高さ）÷2

の公式で求められますので，三角形の面積を変えずに形を変えるには，すなわち三角形の等積変形を行うには，次の図のように１つの底辺に対して高さが変わらないように頂点を移動させるとよい．
　次の図で，高さが変わらないようにするには，頂点A,B,Cが底辺に平行な直線上を動くようにすればよい．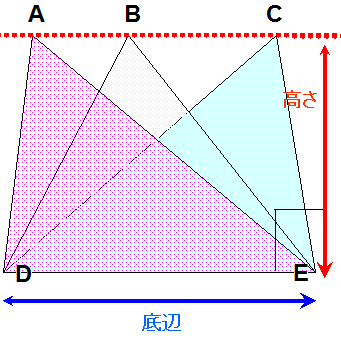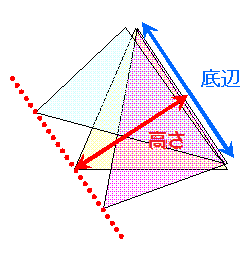

　どの辺を底辺とみなすかは，見る人が自由に決められるから,次の図のように底辺を右上の青線と考えた場合には，その底辺に平行な直線上で残りの頂点を動かすと等積変形になります．

【例１】

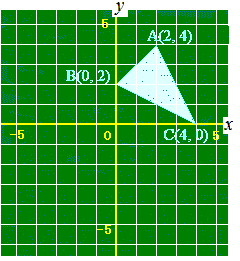　3点A(2, 4), B(0, 2), C(4, 0)を頂点とする△ABCに対して，
(1) y軸のy>2の部分に点P(0, p)をとって△PBCの面積が△ABCの面積と等しくなるようにするには，点P(0, p)のy座標pをどのように定めたらよいか．

(2) x軸上に点Q(q, 0)をとって△QCAの面積が△ABCの面積と等しくなるようにするには，点Q(q, 0)のx座標qをどのように定めたらよいか．ただし，q<4とする．

(3) y軸上に点R(0, r)をとって△RABの面積が△ABCの面積と等しくなるようにするには，点R(0, r)のy座標rをどのように定めたらよいか．ただし，r<2とする．

（解答）

【ポイント】
○　三角形を等積変形するには，頂点を通って底辺に平行な直線を使います．
○　底辺に平行な直線の傾きは，底辺の傾きと同じになります．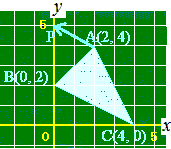

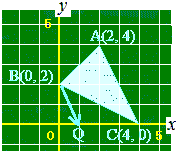
(1)
Aを通ってBCに平行な直線を引くと，ｙ軸と点P(0, 5)で交わるからp=5

正確に言えば，y軸のy<2の部分に点P(0, −1)をとった場合にも，△PBC=△ABCとなるが，やや難しくなるのでy>2の場合に絞った問題にしている．

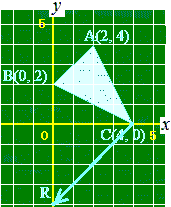
(2)
Bを通ってACに平行な直線を引くと，ｘ軸と点Q(1, 0)で交わるからq=1

正確に言えば，x軸のx>4の部分に点Q(7, 0)をとった場合にも，△QCA=△ABCとなるが，やや難しくなるのでx<4の場合に絞った問題にしている．

(3)
Cを通ってABに平行な直線を引くと，ｙ軸と点R(0, −4)で交わるからr=−4

正確に言えば，y軸のy>2の部分に点R(0, 8)をとった場合にも，△RAB=△ABCとなるが，やや難しくなるのでy<2の場合に絞った問題にしている．

右上に続く

【問題１】 …正しい選択肢をクリックしてください
　3点A(2, 4), B(−1, −2), C(3, 2)を頂点とする△ABCに対して，
(1)　y軸上のy>0の部分に点Pをとって△PBCの面積が△ABCの面積と等しくなるようにするには，点Pのy座標をどのように定めたらよいか解説

−6 −5 −4 −3 −2 −1

0 1 2 3 4 5 6
(2)　x軸上のx<0の部分に点Qをとって△QBCの面積が△ABCの面積と等しくなるようにするには，点Qのx座標をどのように定めたらよいか解説

−6 −5 −4 −3 −2 −1

0 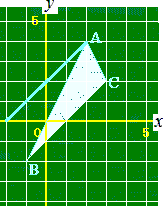1 2 3 4 5 6

Aを通ってBCに平行な直線を引くと，y軸と点P(0, 2)で交わるからy座標は2

Aを通ってBCに平行な直線を引くと，x軸と点Q(−2, 0)で交わるからx座標は−2

　3点A(2, 4), B(−1, −2), C(3, 2)を頂点とする△ABCに対して，
(3)　y軸上のy<0の部分に点Rをとって△RCAの面積が△ABCの面積と等しくなるようにするには，点Rのy座標をどのように定めたらよいか解説

−6 −5 −4 −3 −2 −1

0 1 2 3 4 5 6
(4)　x軸上のx<0の部分に点Sをとって△SCAの面積が△ABCの面積と等しくなるようにするには，点Sのx座標をどのように定めたらよいか解説

−6 −5 −4 −3 −2 −1

0 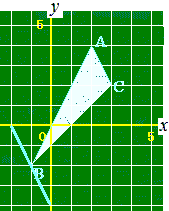1 2 3 4 5 6

Bを通ってACに平行な直線を引くと，y軸と点R(0, −4)で交わるからy座標は−4

Bを通ってACに平行な直線を引くと，x軸と点Q(−2, 0)で交わるからx座標は−2

【例２】
　3点A(4, 7), B(2, 1), C(6, 5)を頂点とする△ABCに対して，
(1) y軸上のy>0の部分に点Pをとって△PBCの面積が△ABCの面積と等しくなるようにするには，点Pのy座標をどのように定めたらよいか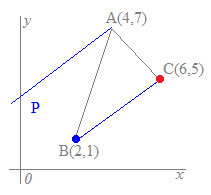

(2) x軸上のx<6の部分に点Qをとって△QCAの面積が△ABCの面積と等しくなるようにするには，点Qのx座標をどのように定めたらよいか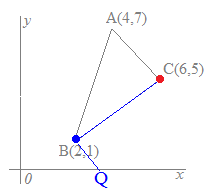

右上に続く

（解答）

　図を書けば答が見えるときもありますが，この例では応用問題になっても解けるように，式を使って解く方法を考えてみます．

(1)

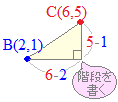○　2点B(2, 1), C(6, 5)を結ぶ底辺BCの傾きmは
$m=\frac{5-1}{6-2}=\frac{4}{4}=1$
で求められます

この計算は，Bの座標からCの座標を引くようにそろえて
$m=\frac{1-5}{2-6}=\frac{-4}{-4}=1$
としても同じになります．分母と分子の両方の符号が変わるので結局同じになります

○　傾き1の直線の方程式は $y=x+ k$
と書けるので，この式に点Aの座標を代入すれば，切片kの値も決まります．
$7=4+ k \rightarrow k=7-4=3$
○　したがって，点Pの座標は(0, 3)

(2)
○　2点A(4, 7), C(6, 5)を結ぶ底辺ACの傾きm'は
$m\apos =\frac{5-7}{6-4}=\frac{-2}{2}=-1$
で求められます
○　傾き−1の直線の方程式は $y=-x+ k\apos$
と書けるので，この式に点Bの座標を代入すれば，切片k'の値も決まります．
$1=-2+ k\apos \rightarrow k\apos =3$
○　直線の方程式は，y=−x+3
この方程式にy=0を代入すればx軸との交点の座標が求まります．
○　0=−x+3 → x=3
　点Qの座標は(3, 0)

【問題２】 …正しい選択肢をクリックしてください
　3点A(3, 4), B(−3, 2), C(2, −3)を頂点とする△ABCに対して，
(1)　y軸上のy>0の部分に点Pをとって△PBCの面積が△ABCの面積と等しくなるようにするには，点Pのy座標をどのように定めたらよいか解説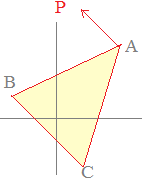

3 4 5 6 7 8

○　2点B(−3, 2), C(2, −3)を結ぶ底辺BCの傾きmは
$m=\frac{-3-2}{2-(-3)}=\frac{-5}{5}=-1$
○　傾き−1の直線の方程式は
$y=-x+ k$
と書けるので，この式に点Aの座標を代入すれば，切片kの値が決まる
$4=-3 + k \rightarrow k=7$
○　したがって，点Pの座標は(0, 7)

　3点A(3, 4), B(−3, 2), C(2, −3)を頂点とする△ABCに対して，
(2)　x軸上のx<0の部分に点Qをとって△QCAの面積が△ABCの面積と等しくなるようにするには，点Qのx座標をどのように定めたらよいか解説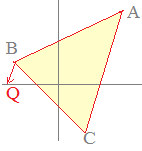

$-\frac{10}{3}$ $-\frac{11}{3}$ $-\frac{16}{5}$ $-\frac{18}{5}$ $-\frac{22}{7}$ $-\frac{23}{7}$

○　2点C(2, −3), A(3, 4)を結ぶ底辺CAの傾きmは
$m=\frac{4-(-3)}{3-2}=7$
○　傾き7の直線の方程式は $y=7x+ k$
と書けるので，この式に点Bの座標を代入すれば，切片kの値が決まる
$2=7\times (-2) + k \rightarrow k=23$
○　点Bを通り傾き7の直線の方程式は
$y=7x + 23$
になるので，この式にy=0を代入すればx軸との交点の座標が求まる
$0=7x + 23 \rightarrow x=-\frac{23}{7}$

右上に続く

【問題３】 …正しい選択肢をクリックしてください
　3点A(3, 5), B(1, 1), C(4, 2)を頂点とする△ABCに対して，
(1)　y=3xの直線上のy>0の部分に点Pをとって△PBCの面積が△ABCの面積と等しくなるようにするには，点Pの座標をどのように定めたらよいか解説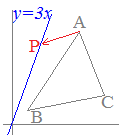

$(\frac{3}{2},\frac{7}{2})$ $(\frac{3}{2},\frac{9}{2})$ $(\frac{5}{2},\frac{7}{2})$ $(\frac{5}{2},\frac{9}{2})$

○　2点B(1, 1), C(4, 2)を結ぶ底辺BCの傾きmは
$m=\frac{2-1}{4-1}=\frac{1}{3}$
○　傾き $\frac{1}{3}$ の直線の方程式は
$y=\frac{1}{3}x+ k$
と書けるので，この式に点Aの座標を代入すれば，切片kの値が決まる
$5=\frac{1}{3}\times 3 + k \rightarrow k=4$
○　直線y=3xと $y=\frac{1}{3}x+ 4$ の交点の座標を，連立方程式を解いて求める．
xを消去すると
$3x=\frac{1}{3}x+ 4$
$9x=x+ 12$
$8x=12$
$x=\frac{3}{2}$
このとき
$y=3\times \frac{3}{2}=\frac{9}{2}$
結局
$P(\frac{3}{2},\frac{9}{2})$

　3点A(3, 5), B(1, 1), C(4, 2)を頂点とする△ABCに対して，
(2)　y=3xの直線上のx<1の部分に点Qをとって△QCAの面積が△ABCの面積と等しくなるようにするには，点Qの座標をどのように定めたらよいか解説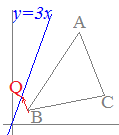

$(\frac{1}{3},\frac{3}{2})$ $(\frac{1}{3},\frac{5}{2})$ $(\frac{2}{3},2)$ $(\frac{2}{3},\frac{7}{2})$

○　2点A(3, 5), C(4, 2)を結ぶ底辺ACの傾きmは
$m=\frac{2-5}{4-3}=-3$
○　傾き $-3$ の直線の方程式は
$y=-3x+ k$
と書けるので，この式に点Bの座標を代入すれば，切片kの値が決まる
$1=-3\times 1 + k \rightarrow k=4$
○　直線y=3xと $y=-3x+ 4$ の交点の座標を，連立方程式を解いて求める．
xを消去すると
$3x=-3x+ 4$
$6x=4$
$x=\frac{4}{6}=\frac{2}{3}$
このとき
$y=3\times \frac{2}{3}=2$
結局
$Q(\frac{2}{3},2)$

←メニューに戻る