|
پ،پ@‰ًگà 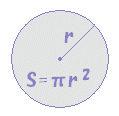
پ@پ›پ@‰~‚ج–تگد‚r‚ً”¼Œa‚’‚ً—p‚¢‚ؤ•\‚ي‚·‚ئپC ‚إ‚·پBپiƒخ‚ح‰~ژü—¦پFƒخ=3.141592...پ©–³Œہ‚ة’·‚¢ڈ¬گ”‚ة‚ب‚é‚©‚çƒMƒٹƒVƒƒ•¶ژڑƒخ‚إ•\‚·‚±‚ئ‚ة‚ب‚ء‚ؤ‚¢‚éپj 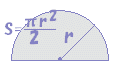 پ@پ›پ@”¼‰~‚ج–تگد‚حپC‰~‚ج–تگد‚ج”¼•ھ‚¾‚©‚ç
پ@پ›پ@”¼‰~‚ج–تگد‚حپC‰~‚ج–تگد‚ج”¼•ھ‚¾‚©‚ç پ@پ›پ@‚R•ھ‚ج‚P‰~‚ج–تگد‚حپC‰~‚ج–تگد‚ج3•ھ‚ج‚P‚¾‚©‚ç
پ@پ›پ@‚R•ھ‚ج‚P‰~‚ج–تگد‚حپC‰~‚ج–تگد‚ج3•ھ‚ج‚P‚¾‚©‚ç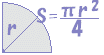 پ@پ›پ@‚S•ھ‚ج‚P‰~‚ج–تگد‚حپC‰~‚ج–تگد‚ج‚S•ھ‚ج‚P‚¾‚©‚ç
پ@پ›پ@‚S•ھ‚ج‚P‰~‚ج–تگد‚حپC‰~‚ج–تگد‚ج‚S•ھ‚ج‚P‚¾‚©‚çپ@پ›پ@ˆê”ت‚ة’†گSٹp 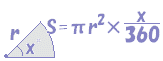
|
پ،پ@—ل‘è1
”¼Œa‚ھa(cm2)‚إ’†گSٹp‚ھ45پ‹‚جگîŒ`‚ج–تگدS(cm2)‚ح
پ،پ@—ل‘è2
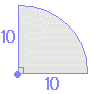
‰Eگ}‚ج‚و‚¤‚ة”¼Œaa(cm)‚ج‰~‚ئ‚±‚ê‚ة‚ةٹOگع‚·‚éگ³•ûŒ`پi1•س‚ج’·‚³‚ح2a(cm)پj‚إˆح‚ـ‚ꂽژخگü•”‚ج–تگد‚ح 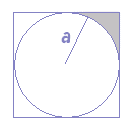
پ@پ@گ³•ûŒ`‚ج–تگد‚ھ4a2 پ@پ@‰~‚ج–تگد‚ھƒخa2 ‚¾‚©‚ç پ@پ@ 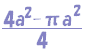
|
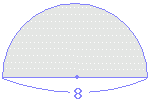
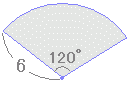
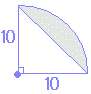


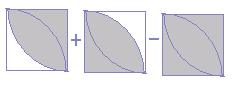

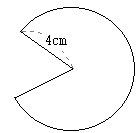
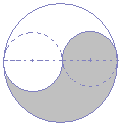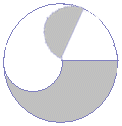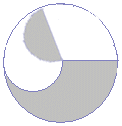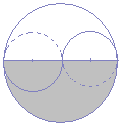 گ}‚ج‚و‚¤‚ةڈ¬‚³‚¢‰~‚ج”¼•ھ‚ً‰ٌ“]‚³‚¹‚é‚ئپC“ت‚ج•”•ھ‚ھ‚؟‚ه‚¤‚ا‰ڑ‚ج•”•ھ‚ةڈd‚ب‚é‚©‚çپC‘ه‚«‚¢‰~‚ج–تگد‚ج”¼•ھ‚ً‹پ‚ك‚é‚ئ‚و‚¢
گ}‚ج‚و‚¤‚ةڈ¬‚³‚¢‰~‚ج”¼•ھ‚ً‰ٌ“]‚³‚¹‚é‚ئپC“ت‚ج•”•ھ‚ھ‚؟‚ه‚¤‚ا‰ڑ‚ج•”•ھ‚ةڈd‚ب‚é‚©‚çپC‘ه‚«‚¢‰~‚ج–تگد‚ج”¼•ھ‚ً‹پ‚ك‚é‚ئ‚و‚¢
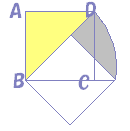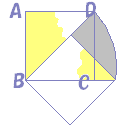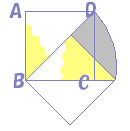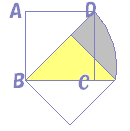 ‰©گF‚إژ¦‚µ‚½’¼ٹp“ٌ“™•سژOٹpŒ`‚ح‰ٌ“]‚µ‚ؤڈd‚ب‚éپD
‰©گF‚إژ¦‚µ‚½’¼ٹp“ٌ“™•سژOٹpŒ`‚ح‰ٌ“]‚µ‚ؤڈd‚ب‚éپD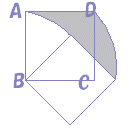
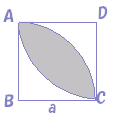
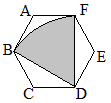
 پ@ڈم‚ج–â‘è‚S‚جŒ‹‰تپi–â‘è‚جگ}‚حڈم‚جچ¶‘¤پj‚©‚çپCژں‚جگ}‚ج‰©گF‚إژ¦‚µ‚½گ}Œ`‚ج–تگد‚ًˆّ‚‚ئ‚و‚¢پD
پ@ڈم‚ج–â‘è‚S‚جŒ‹‰تپi–â‘è‚جگ}‚حڈم‚جچ¶‘¤پj‚©‚çپCژں‚جگ}‚ج‰©گF‚إژ¦‚µ‚½گ}Œ`‚ج–تگد‚ًˆّ‚‚ئ‚و‚¢پD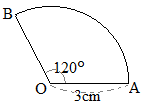
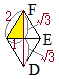 ‰Eگ}‚ة‚و‚è
‰Eگ}‚ة‚و‚è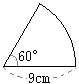
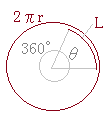 ”¼Œa
”¼Œa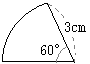 پ@‰E‚جگ}‚ج‚و‚¤‚بپC”¼Œa‚ھ3cmپC’†گSٹp‚ھ60پ‹‚ج‚¨‚¤‚¬Œ`OAB‚ھ‚ ‚éپB‚±‚ج‚¨‚¤‚¬Œ`‚جŒت‚ج’·‚³‚ً‹پ‚ك‚ب‚³‚¢پB‚½‚¾‚µپC‰~ژü—¦‚ح
پ@‰E‚جگ}‚ج‚و‚¤‚بپC”¼Œa‚ھ3cmپC’†گSٹp‚ھ60پ‹‚ج‚¨‚¤‚¬Œ`OAB‚ھ‚ ‚éپB‚±‚ج‚¨‚¤‚¬Œ`‚جŒت‚ج’·‚³‚ً‹پ‚ك‚ب‚³‚¢پB‚½‚¾‚µپC‰~ژü—¦‚ح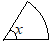 پ@‰E‚جگ}‚حپC”¼Œa‚ھ4cmپCŒت‚ج’·‚³‚ھ
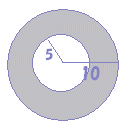
پ@‰E‚جگ}‚حپC”¼Œa‚ھ4cmپCŒت‚ج’·‚³‚ھ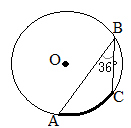 پ@‰E‚جگ}‚ج‚و‚¤‚ةپC”¼Œa‚ھ10cm‚ج‰~O‚جژüڈم‚ةپC3“_AپCBپCC‚ًپعABC=36پ‹‚ئ‚ب‚é‚و‚¤‚ة‚ئ‚è‚ـ‚·پB‚±‚ج‚ئ‚«پC‘¾‚¢گü‚إژ¦‚µ‚½
پ@‰E‚جگ}‚ج‚و‚¤‚ةپC”¼Œa‚ھ10cm‚ج‰~O‚جژüڈم‚ةپC3“_AپCBپCC‚ًپعABC=36پ‹‚ئ‚ب‚é‚و‚¤‚ة‚ئ‚è‚ـ‚·پB‚±‚ج‚ئ‚«پC‘¾‚¢گü‚إژ¦‚µ‚½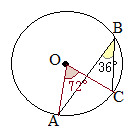 پ@’†ٹw2”N‚إڈK‚¤پu‰~ژüٹp‚ج’è—پv‚ة‚و‚èپC’†گSٹp‚ح‰~ژüٹp‚ج2”{‚إ‚·پD‚µ‚½‚ھ‚ء‚ؤپCپعABC=36پ‹‚ج‚ئ‚«پعAOC=72پ‹‚إ‚·پD
پ@’†ٹw2”N‚إڈK‚¤پu‰~ژüٹp‚ج’è—پv‚ة‚و‚èپC’†گSٹp‚ح‰~ژüٹp‚ج2”{‚إ‚·پD‚µ‚½‚ھ‚ء‚ؤپCپعABC=36پ‹‚ج‚ئ‚«پعAOC=72پ‹‚إ‚·پD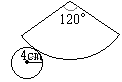 پ@‰E‚جگ}‚ح‰~
پ@‰E‚جگ}‚ح‰~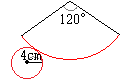 ‰Eگ}‚جگش‚إژ¦‚µ‚½گü‚ج’·‚³پC‚·‚ب‚ي‚؟’ê–ت‚ج‰~ژü‚ج’·‚³‚ئ‘¤–ت‚ج‚¨‚¤‚¬Œ`‚جŒت‚ج’·‚³‚ح“™‚µ‚¢پD
‰Eگ}‚جگش‚إژ¦‚µ‚½گü‚ج’·‚³پC‚·‚ب‚ي‚؟’ê–ت‚ج‰~ژü‚ج’·‚³‚ئ‘¤–ت‚ج‚¨‚¤‚¬Œ`‚جŒت‚ج’·‚³‚ح“™‚µ‚¢پD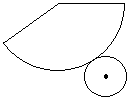 پ@‰E‚جگ}‚حپC‰~
پ@‰E‚جگ}‚حپC‰~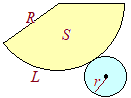 ‚¨‚¤‚¬Œ`‚ج”¼Œa‚ً
‚¨‚¤‚¬Œ`‚ج”¼Œa‚ً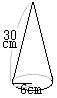 پ@‰E‚جگ}‚حپC’ê–ت‚ج”¼Œa‚ھ6cmپC•êگü‚ج’·‚³‚ھ30cm‚ج‰~‚·‚¢‚إ‚ ‚éپB‚±‚ج‰~‚·‚¢‚ج“WٹJگ}‚ً‚©‚¢‚½‚ئ‚«پC‘¤–ت‚ة‚ب‚邨‚¤‚¬Œ`‚ج’†گSٹp‚ً‹پ‚ك‚ب‚³‚¢پB
پ@‰E‚جگ}‚حپC’ê–ت‚ج”¼Œa‚ھ6cmپC•êگü‚ج’·‚³‚ھ30cm‚ج‰~‚·‚¢‚إ‚ ‚éپB‚±‚ج‰~‚·‚¢‚ج“WٹJگ}‚ً‚©‚¢‚½‚ئ‚«پC‘¤–ت‚ة‚ب‚邨‚¤‚¬Œ`‚ج’†گSٹp‚ً‹پ‚ك‚ب‚³‚¢پB
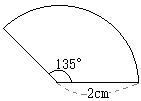
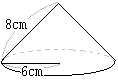 پ@‰E‚جگ}‚حپC’ê–ت‚ج”¼Œa‚ھ6cmپC•êگü‚ج’·‚³‚ھ8cm‚ج‰~‚·‚¢‚إ‚ ‚éپB‚±‚ج‰~‚·‚¢‚ج“WٹJگ}‚ً‚©‚¢‚½‚ئ‚«پC‘¤–ت‚ة‚ب‚邨‚¤‚¬Œ`‚ج–تگد‚ً‹پ‚ك‚ب‚³‚¢پB
پ@‰E‚جگ}‚حپC’ê–ت‚ج”¼Œa‚ھ6cmپC•êگü‚ج’·‚³‚ھ8cm‚ج‰~‚·‚¢‚إ‚ ‚éپB‚±‚ج‰~‚·‚¢‚ج“WٹJگ}‚ً‚©‚¢‚½‚ئ‚«پC‘¤–ت‚ة‚ب‚邨‚¤‚¬Œ`‚ج–تگد‚ً‹پ‚ك‚ب‚³‚¢پB