|
現在地と前後の項目 平行線と線分の比/相似図形を探す問題1/相似図形を探す問題2/相似図形を作る問題/相似図形と辺の比/相似，平行線と比/中点連結定理1/中点連結定理2/問題以上,答以下/入試問題1/入試問題2/入試問題3/入試問題4/証明の進め方5/角の二等分線と補助線/面積比/メネラウスの定理,チェバの定理/ ■相似図形と辺の比→ 印刷用PDF版は別頁
【相似図形の性質】
相似図形については，３組の辺の比が等しくなる． ⇒ この公式を使って辺の長さを求めることができる．
例
右図１でAB//CD のとき，△AEB と△DEC が相似図形になるので
（証明）
AB:DC=AE:DE=BE:CE
が成り立つ．△AEBと△DECについて ∠AEB=∠DEC …（対頂角は等しい） ∠ABE=∠DCE …（平行線の錯角は等しい） だから，△AEBと△DEC は相似図形 そこで BE:CE を求めたいときは，AB:DC の比3:2 を書けばよい．（♪～「辺の比は相似比で答える」～♪）
もちろん，これは辺の長さが BE=3 とか CE=2 などということではない．比が3:2 ということは，実際の長さとしては 6 と4，9 と6，12 と8 などいろいろな場合があるが，ここでは「長さは決まらなくても比だけなら求められる問題」を扱っている．
上の例のように，♪～「辺の比は相似比で答える」～♪とよい
【要点】
辺の比 BE:CE を求めたいときは，
(1) その線分が辺になっている２つの相似図形△AEB と△DEC を見つける (2) すでに辺の比が分かっている他の辺の比 AB:DC を答える |
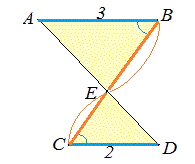 図1 |
|
例題１
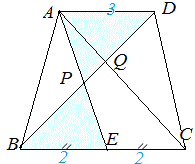 右図２において AD//BC ，AD=3 ，BC=4 ，E は BC の中点，対角線 BD と AE ，AC の交点を各々 P ，Q とするとき，(1) BP:PD は△APD と△EPB を見れば分かるから，2:3 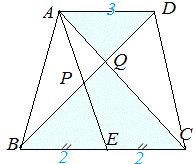 (2) BQ:QD は△AQD と△CQB を見れば分かるから，4:3(3) BP:PQ は(1)(2)から次のように計算で求められる．
ただし，2:3 や 4:3 は実際の長さを表しているわけではないので，このまま使うことはできない．そこで，何か共通の基準「たとえば辺 BD の長さ」で表すことを考える．
BP:PD=2:3 だから BP=  25BDBQ:QD=4:3 だから BQ= 47BDゆえに，BP:BQ= 25BD : 47BD = 25 : 47 = 1435 : 2035 =14:20結局 BP:PQ=14:(20 -14)=14:6=7:3 …（答） |
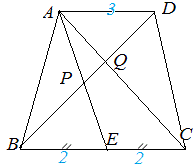 図２ |
|
問題１ （もっとも簡単な整数比で答えなさい．）
|
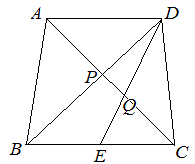
(1) △APD ∽△CPB だから
AP:PC=AD:CB=5:6…（答）
(2) △AQD ∽△CQE だから
AQ:QC=AD:CE=5:3…（答）
(3)
AP= 511ACAQ= 58ACだから AP:AQ= 511AC : 58AC= 511 : 58 = 4088 : 5588 =40:55=8:11AP:PQ=8:(11-8)=8:3 …（答） |
|
問題２ （もっとも簡単な整数比で答えなさい．）
|
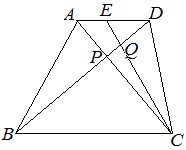
(1) △APD ∽△CPB だから
BP:PD=BC:DA=7:5…（答）
(2) △EQD ∽△CQB だから
BQ:QD=BC:DE=7:3…（答）
(3)
BP= 712BDBQ= 710BDだから BP:BQ= 512BD : 710BD= 712 : 710 = 3560 : 4260 =35:42=5:6BP:PQ=5:(6-5)=5:1 …（答） |
|
問題３ （もっとも簡単な整数比で答えなさい．）
|
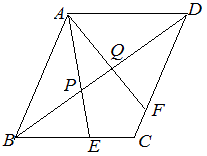
(1) △APD ∽△EPB だから
BP:PD=BE:DA=3:5…（答）
(2) △BQA ∽△DQF だから
BQ:QD=BA:DF=6:5…（答）
(3)
BP= 38BDBQ= 611BDだから BP:BQ= 38BD : 611BD= 38 : 611 = 3388 : 4888 =33:48=11:16BP:PQ=11:(16-11)=11:5 …（答） |