|
■根号計算（約分）
２次方程式の解の公式を使うためには，根号計算，特に「根号を含む分数」の約分が正確にできなければなりません．この頁では解の公式を使ったときに登場する「根号を含む分数」の約分を練習します．
【例１】次の式を約分して簡単にしてください．
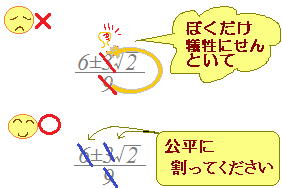
【解答】= （注意） 分母を３で割るときは，分子のどの項もすべて３で割らなければなりません．次の例はよくある間違いで，分子の内の一部分だけを３で割っているところが間違いです． は間違い は間違い ※上のような間違いを避けるために，「約分する前には必ず（ ）でくくる」（かっこでくくっていない式は約分しない）と決めると安全に約分ができます． == |
 |
|
次の式を約分して簡単にしてください．（正しいものを下の選択肢から選んでください．）
1± |
6, 2, 8はいずれも2で割り切れるので（最大公約数は2だから），分母・分子を2で割ります．
= ※「約分する前に（ ）でくくる」方式で行うときは == |
|
1±3 3± |
6, 3, 6はいずれも3で割り切れるので（最大公約数は3だから），分母・分子を3で割ります．
= ※「約分する前に（ ）でくくる」方式で行うときは == |
|
−3± −1±3 |
3, 6, 6はいずれも3で割り切れるので（最大公約数は3だから），分母・分子を3で割ります．
= ※「約分する前に（ ）でくくる」方式で行うときは == |
|
2± 2±6 3±4 4±3 12± |
12, 6, 6はいずれも6で割り切れるので（最大公約数は6だから），分母・分子を6で割ります．
=2± ※「約分する前に（ ）でくくる」方式で行うときは ==2± |
|
−2±9 −6±9 −2±3 −2±9 −6±3 |
6, 9, 3はいずれも3で割り切れるので（最大公約数は3だから），分母・分子を3で割ります．
=−2±3 ※「約分する前に（ ）でくくる」方式で行うときは ==−2± |
|
【例２】次の式を約分して簡単にしてください．
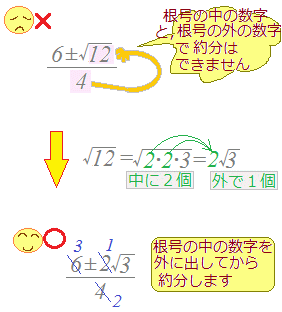
【解答】==
根号の中の数を素因数分解したときに２個ある数は，根号の外に出したときに１個になります．
例==2 根号の中に３個ある数は，２個だけ出せます． 例==3 根号の中に４個ある数は，根号の外に出したときに２個になります． 例==22=4 ２種類以上の数字が外に出ることもあります． 例==2×3=6 |
 |
|
1± 3± 6± |
はじめに，を変形しておきます．
==3 次に，6, 3, 6はいずれも3で割り切れるので（最大公約数は3だから），分母・分子を3で割ります． = |
|
12±1 4± |
はじめに，を変形しておきます．
==3 次に，12, 3, 27はいずれも3で割り切れるので（最大公約数は3だから），分母・分子を3で割ります． = |
|
−4± −4± −4± −8± −8± |
はじめに，を変形しておきます．
==2 次に，8, 2, 2はいずれも2で割り切れるので（最大公約数は2だから），分母・分子を2で割ります． =−4± |
|
【例３】次の式を約分して簡単にしてください．
【解答】=だから−1, 2
根号が完全にはずれるもの ⇒ 分ければ簡単になる．
分ければ簡単になるものは分けて答える． 根号の中に数字が残るもの ⇒ 分けても簡単にならない． 分けても簡単にならないものは±のまま答える． |
は２つの数字, をまとめて書いたものなので， ==−1 ==2 のように「分けて書けば簡単になります」． このように
分ければ簡単になるものは，分けて答えます．
これに対して，上で扱ってきたのような数字は，分けてもとにしかなりませんので， もととほとんど同じになり分ける値打がありません． |
|
1, 2 5, 7 , 3± |
はじめに，を変形しておきます．
=2 次に，6±2を6−2=4, 6+2=8に分けて計算します． =1, =2 |
|
2, 3 12, 18 |
はじめに，を変形しておきます．
=3 次に，15±3を15−3=12, 15+3=18に分けて計算します． =2, =3 |
|
−10, 0 −, 0 |
はじめに，を変形しておきます．
=5 次に，−5±5を−5−5=−10, −5+5=0に分けて計算します． =−, =0 |
|
【例４】次の式を約分して簡単にしてください．
【解答】= ※ 分母は「なるべく」正の数になるようにします．（高校以上では様々な場面で，分母を負の数のまま使うこともありますが，中学校の基本の段階では，「分母は正の数にする」ように決める方がよい．） ※ 上の式で，分母と分子を−2で割ると，それぞれ符号が変わりますので 分子は−1  3分母は2 となりますが，順序を問題にしないときは単に と書けばよい． |
※高校で連立方程式の解を表すときなどにおいて， (−3, 4), (3, −4)のような組をまとめて書くときは， (±3, 4)（複号同順）と書きます．これは± という複号を読むときに，上と上，下と下が組であることを表しています．だから(±3, 4)（複号同順）と書かれているときに(−3, −4), (3, 4)は入りません．同様にして(±3, ±4)（複号同順）と書かれているときは(−3, −4), (3, 4)の組を表しています． 中学校で，解の公式を使って２つの数字の組が出てきただけなら順序は問題にならないので，複号同順などと書く必要はなく，左の解答のように順序を気にすることはなく，±を負の数で割っても±のまま使えばよい． |
|
|
分母・分子を−2で割って約分します．
= |
|
−15±2 |
分母・分子を−5で割って約分します．
= |