|
== 証明の進め方 ==(平行四辺形の証明問題) ○はじめに 「2組の向かい合う辺がそれぞれ平行である四角形」を平行四辺形という.(平行四辺形の定義)この頁では平行線の性質について,1つの性質から他の性質を証明する場合を例にとって,仮定と結論の選び方を練習する.(仮定と結論が分かれば証明の入口と出口が分かるので,これにそって実際の証明を考えていくことになる.) 例1 「平行四辺形であるならば2組の向かい合う辺はそれぞれ等しい」という性質※を証明したいときは,
仮定「平行四辺形」
を示せばよい.から 結論「2組の向かい合う辺はそれぞれ等しい」 「平行四辺形」を定義にしたがって「2組の向かい合う辺がそれぞれ平行である四角形」に置き換えると,式としては
「AD//BC , AB//DC」を仮定とし
ことになる.「AD=BC , AB=DC」を結論とする |
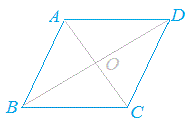
「四角形の対角線がそれぞれの中点で交わるならば1組の向かい合う辺が等しくて平行になる」という性質を証明したいときは,
仮定「四角形の対角線がそれぞれの中点で交わる」
を示せばよい.から 結論「1組の向かい合う辺が等しくて平行になる」 式としては
「AO=CO , BO=DO」を仮定とし
ことになる.
「AD=BC , AD//BC」を結論とする. (「AB=DC , AB//DC」を結論に選んでもよい) ※例1のような性質は「平行四辺形の2組の向かい合う辺はそれぞれ等しい」と表現されることもある. |
|
■問題 四角形ABCDについて左欄の性質を証明するとき,どのような仮定からどのような結論を導けばよいか.右の欄から選びなさい. (はじめに左欄の問題を1つ選び続けて右欄の答えを選びなさい.なお,証明方法は他にもありますが右欄の中では1つです.) |
|