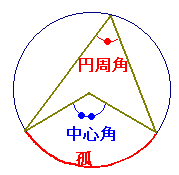
【円周角の定理】一つの孤に対する「円周角」の大きさは，「中心角」の半分になります． |
《問題》 |
(2) 
図の赤で示した弧に対する円周角は等しいから，黄色で示した三角形の１つの角が30°だと分かります．これを使って，ｂ=30°+50°=80°が求まります． （黄色の三角形の内角の和から残りの角を求めて，180°から引いてもよい） |
(3)
円の中心を通る直線で黄色で示した三角形を２つに分けると，それぞれが二等辺三角形になります．（半径が等しいから）そうすると，上端の角が20°+30°=50°になります． 次に，中心角は円周角の2倍だから，ｃ=100° |